
- •Аналітична геометрія Індивідуальні завдання
- •Завдання для індивідуальної роботи модуль б (рік навчання 1, семестр 2)
- •Завдання № 1 Системи координат у просторі
- •Завдання № 2 Застосування методу координат до розв’язування задач елементарної геометрії
- •Завдання № 3 Рівняння площини
- •Завдання № 4 Взаємне розміщення площин
- •Завдання № 5 Метричні задачі з теорії площин
- •Завдання № 6 Канонічні рівняння прямої у просторі
- •Завдання № 10 Застосування теорії прямих і площин до розв’язування задач елементарної геометрії
- •Завдання № 11 Циліндричні поверхні
- •Завдання № 12 Конічні поверхні
- •Завдання № 13 Поверхні обертання
- •Завдання № 14 Еліпсоїд. Параболоїди. Гіперболоїди
- •Завдання № 20 Рухи простору. Перетворення подібності
Завдання № 6 Канонічні рівняння прямої у просторі
Скласти рівняння прямої, що утворена перетином площини
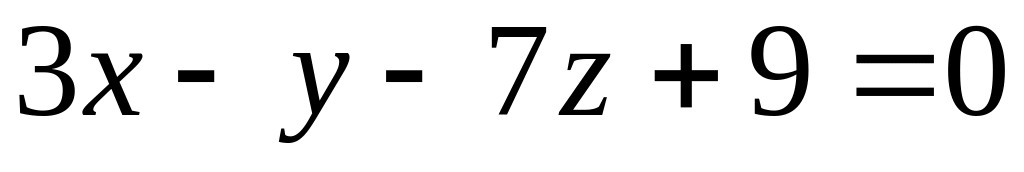 з площиною, що проходить через вісь Ох
і точку
з площиною, що проходить через вісь Ох
і точку
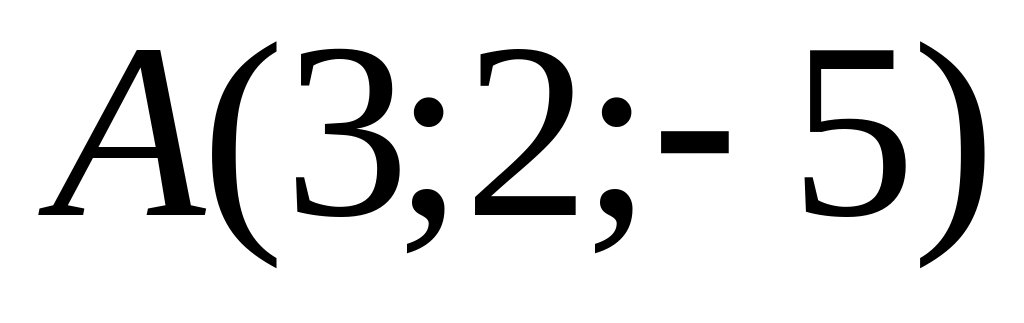 .
.Вершини трикутника знаходяться в точках А(3;6;-7), В(-5;2;3), С(4;-7;-2). Скласти параметричні рівняння прямої, яка містить медіану трикутника, проведену з вершини С.
Вершини трикутника знаходяться в точках А(3;-1;-1), В(1;2;-7), С(-5;14;-3). Скласти канонічні рівняння прямої, яка містить бісектрису внутрішнього кута С трикутника.
Вершини трикутника знаходяться в точках А(1;-2;-4), В(3;1;-3), С(5;1;-7). Скласти канонічні рівняння прямої, яка містить висоту трикутника, опущену з вершини В на протилежну сторону.
Скласти канонічні рівняння прямої, що проходить через точку М1(2;3;-5) паралельно прямій
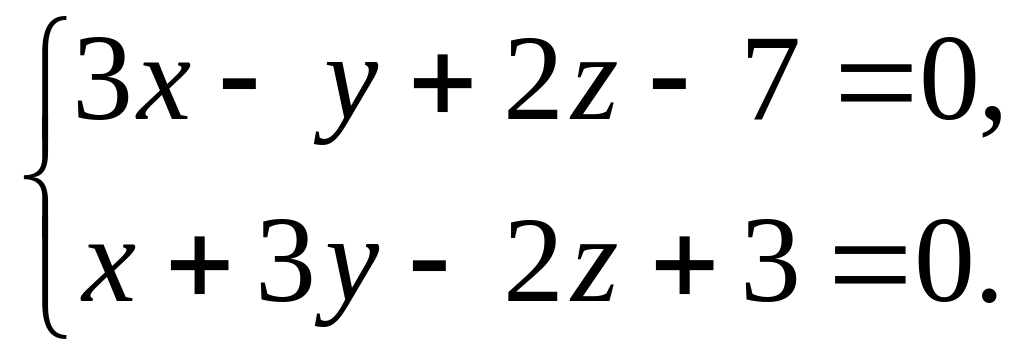
Скласти рівняння прямої, яка проходить через точку М1(-1;2;-3) перпендикулярно до вектора
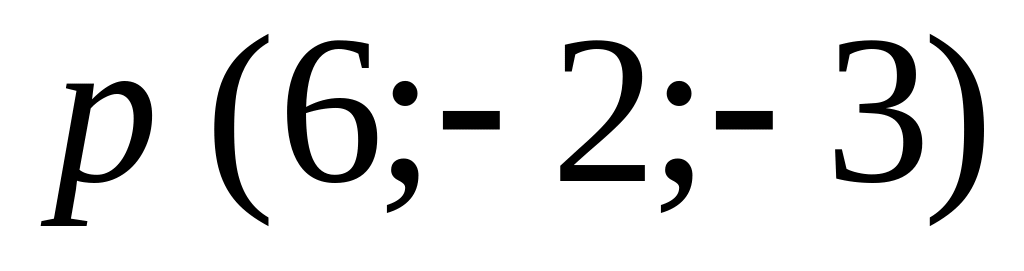 і перетинає пряму
і перетинає пряму
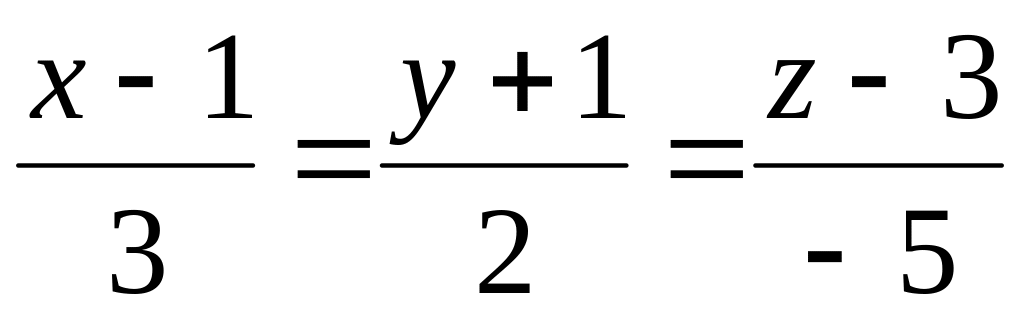 .
.Скласти рівняння прямої, яка проходить через точку М(-4;-5;3) і перетинає дві прямі
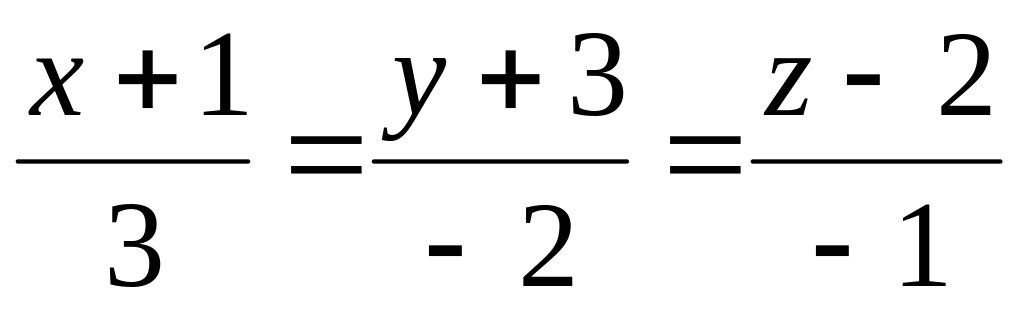 і
і
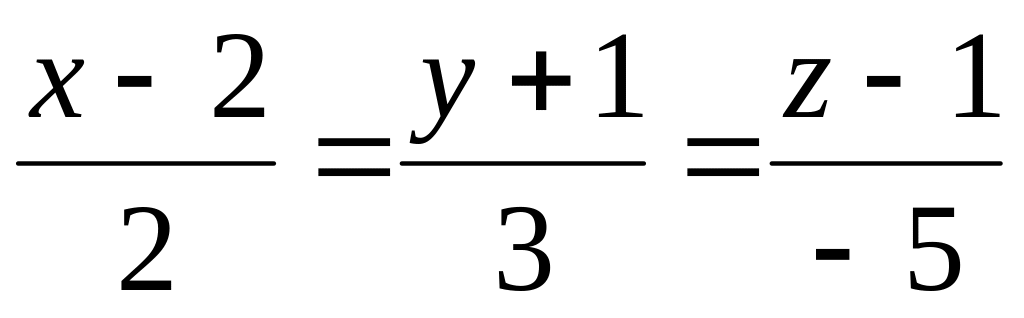 .
.Скласти канонічні рівняння прямої, яка містить спільний перпендикуляр двох прямих, заданих рівняннями
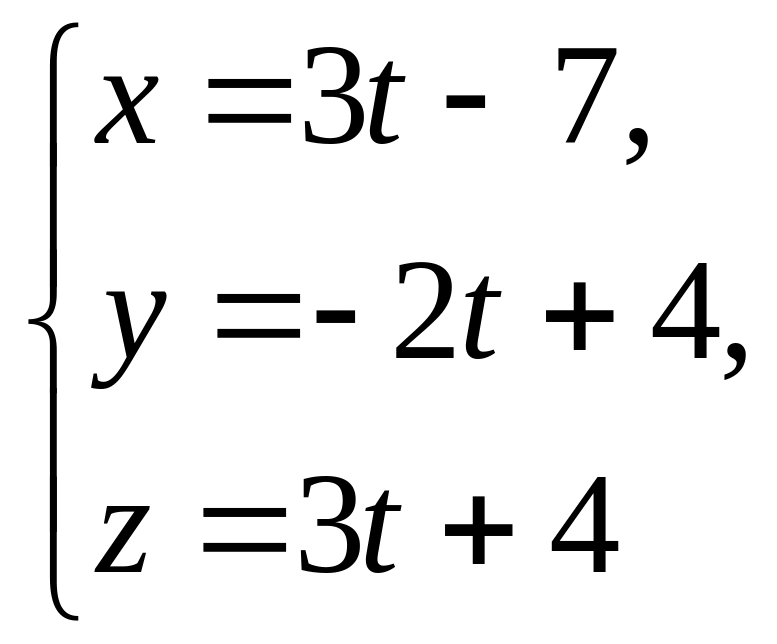 і
і
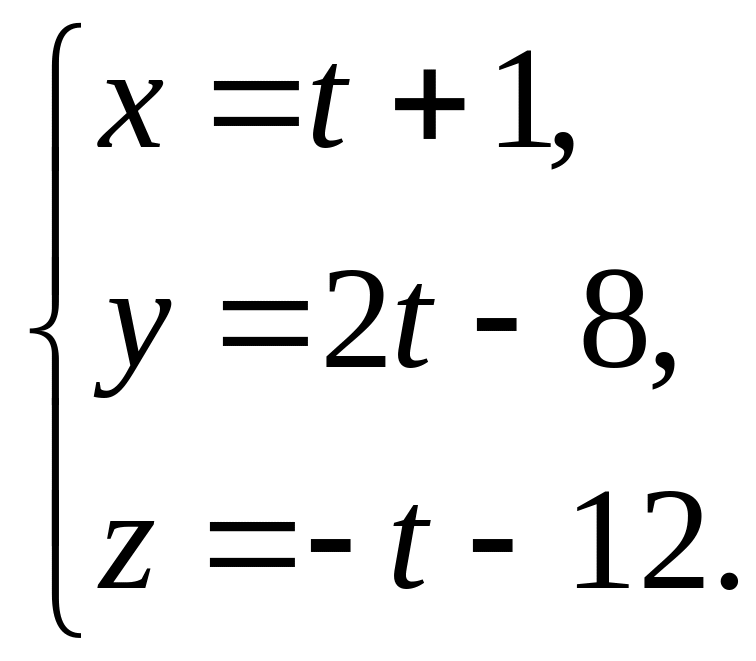
Скласти рівняння прямої, яка лежить у площині
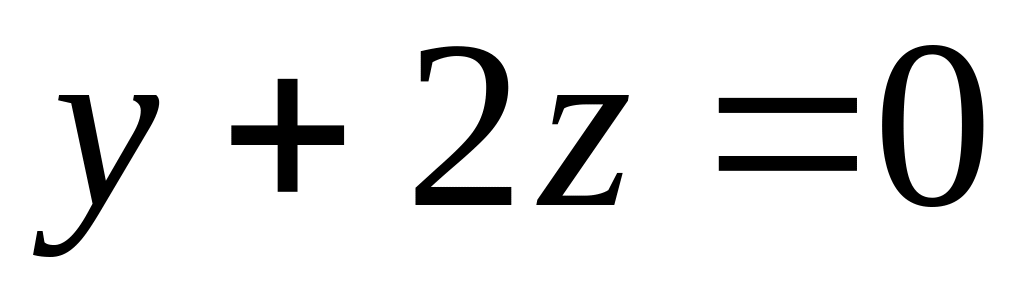 і перетинає прямі
і перетинає прямі
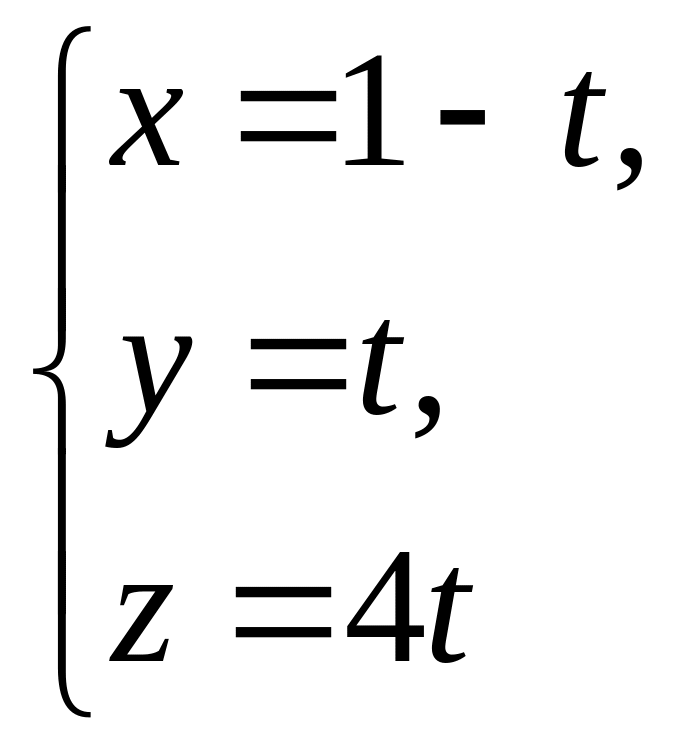 та
та
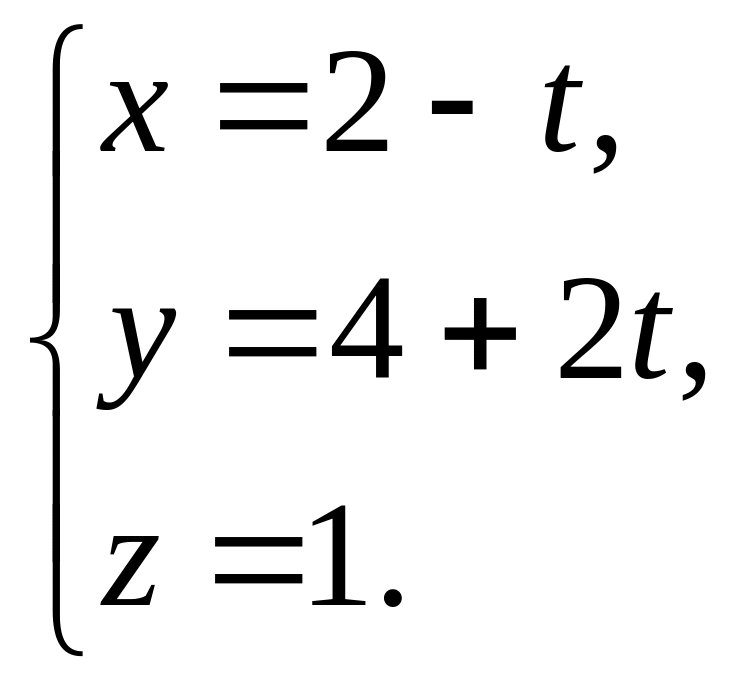
Знайти рівняння проекції прямої
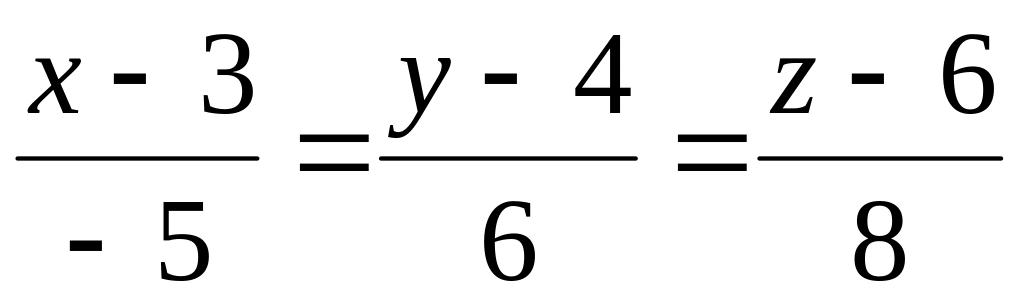 на площину Оху.
на площину Оху.
ЗАВДАННЯ № 7
Параметричні рівняння прямої у просторі
Скласти параметричні рівняння прямої, яка проходить через точку М0 паралельно прямій l.
1. М0
(2;-1;3), l:
![]()
2. М0
(1;0;4), l:
![]()
3. М0
(0;1;-3), l:
![]()
4. М0
(-2;1;5), l:
![]()
5. М0
(2;0;-1), l:
![]()
6. М0
(-1;3;0), l:
![]()
7. М0
(1;-3;-1),
l:
![]()
8. М0
(3;-1;2), l:
![]()
9. М0
(-1;3;6), l:
![]()
10. М0
(5;0;-2), l:
![]()
ЗАВДАННЯ № 8
Взаємне розміщення прямих у просторі
Встановити взаємне розміщення прямих у просторі:
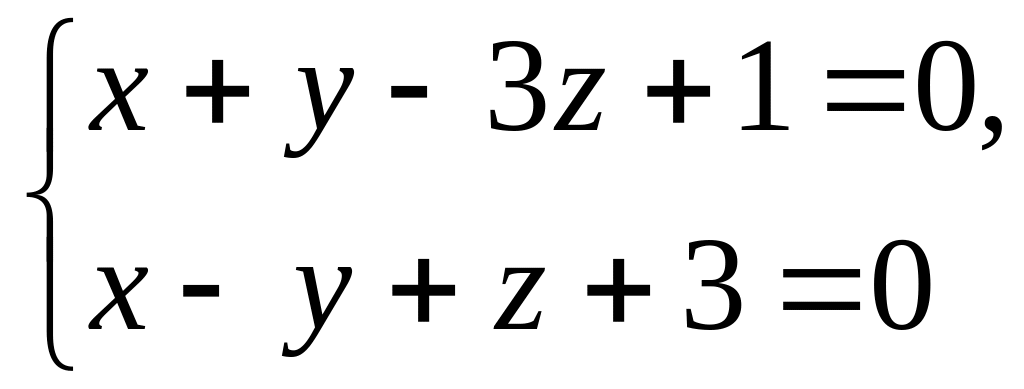 і
і
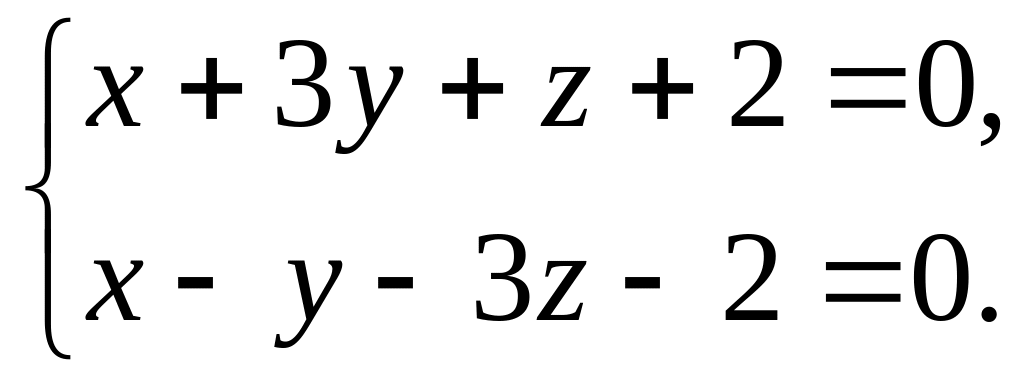
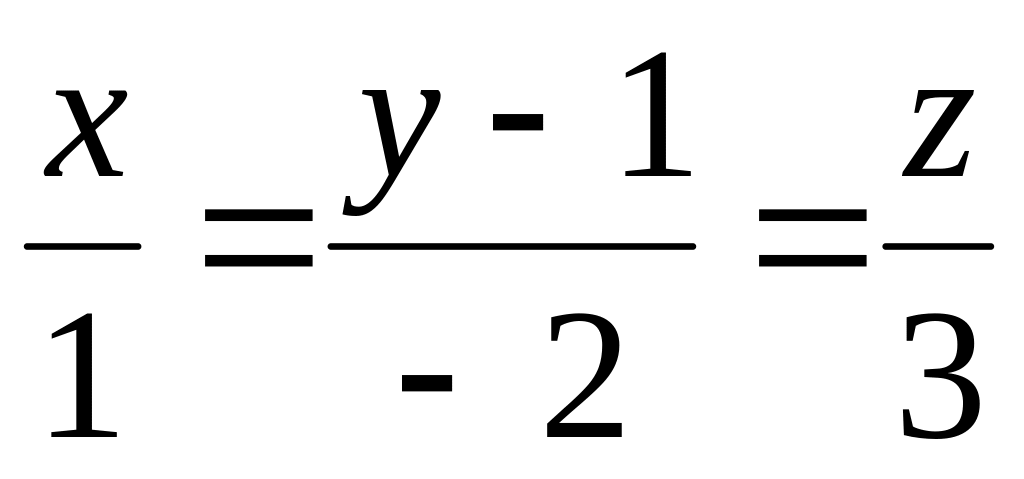 і
і
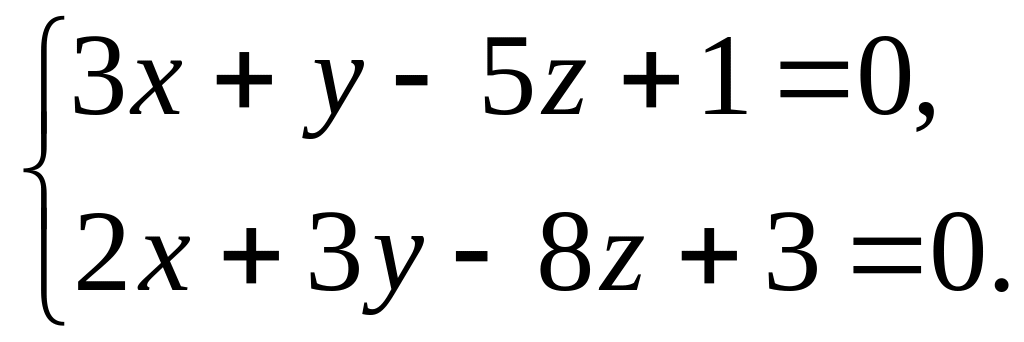
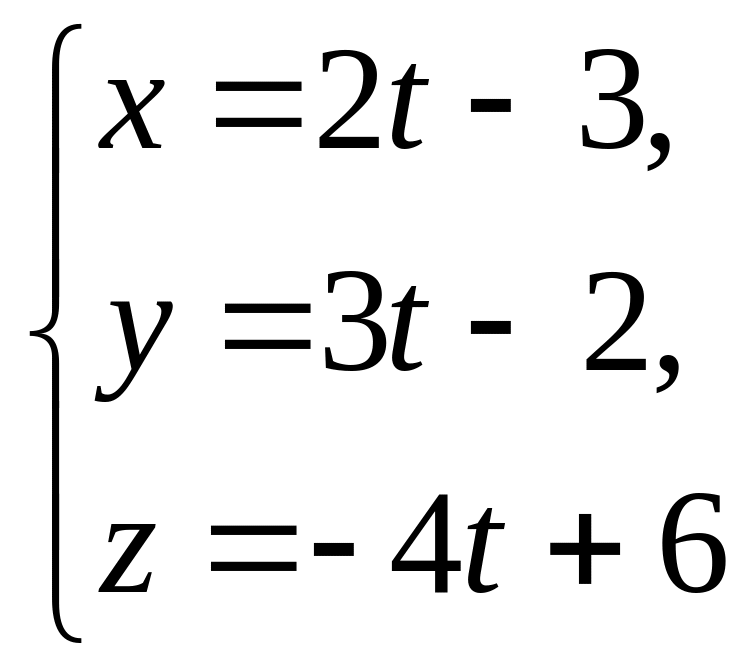 і
і
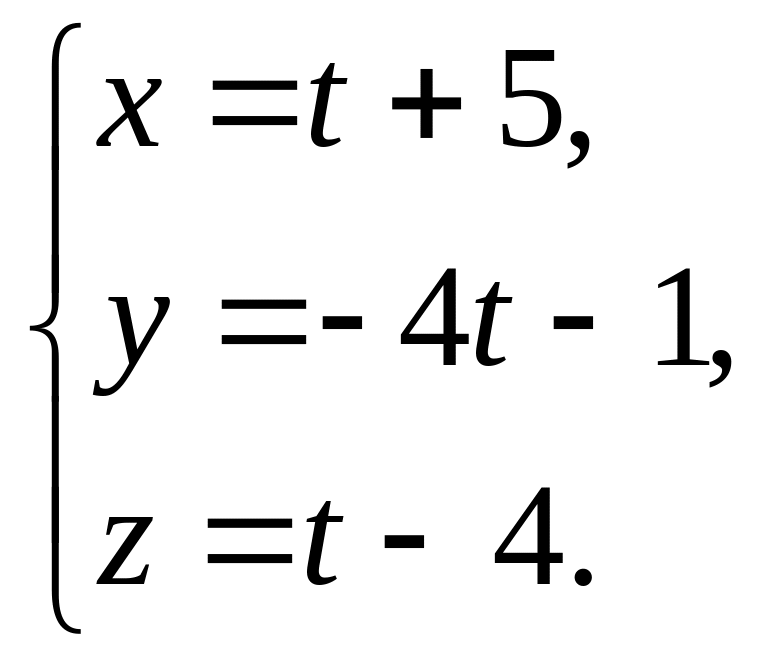
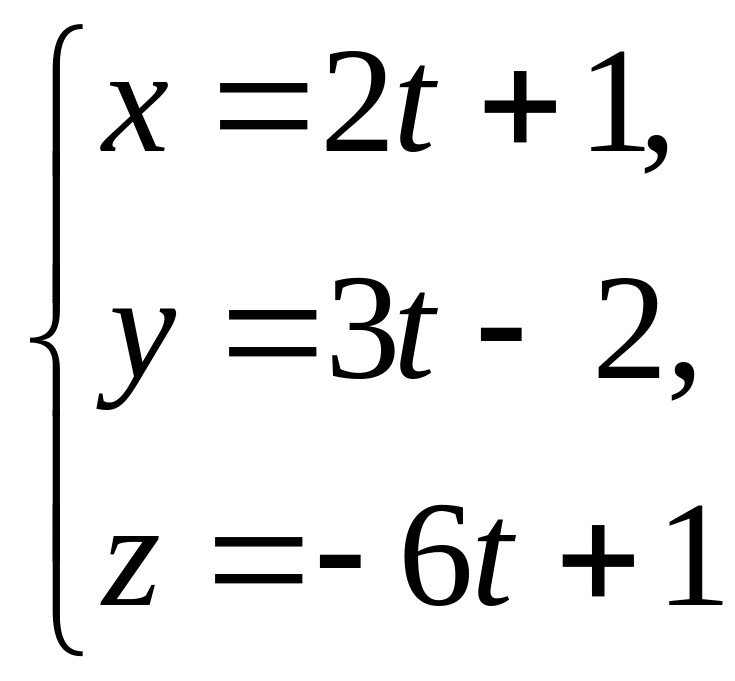 і
і
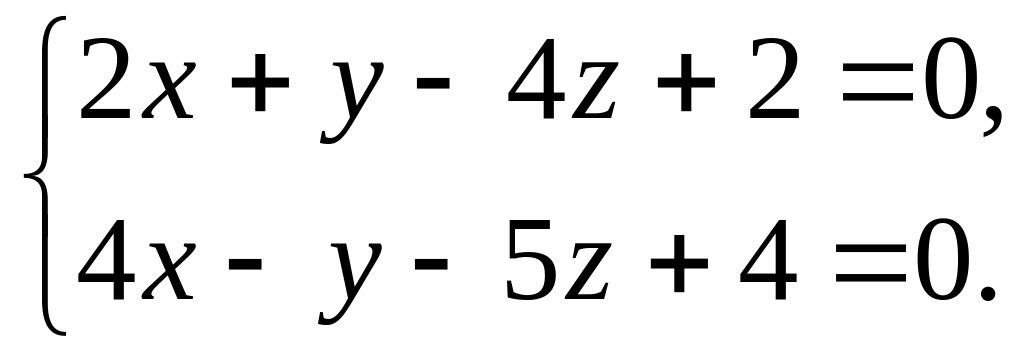
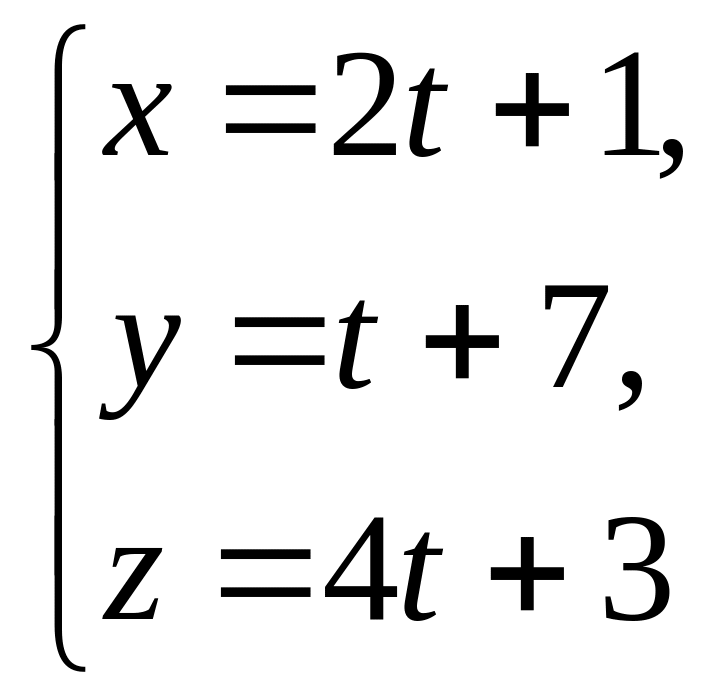 і
і
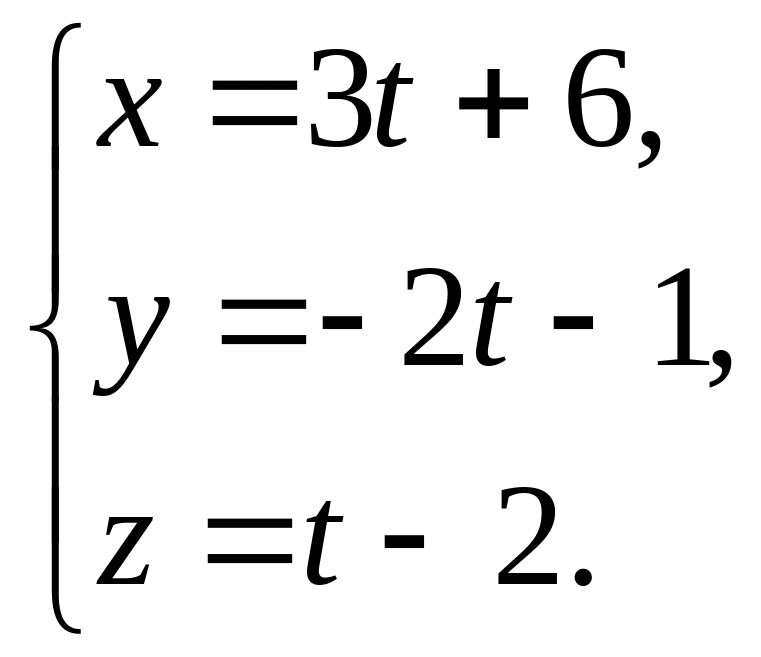
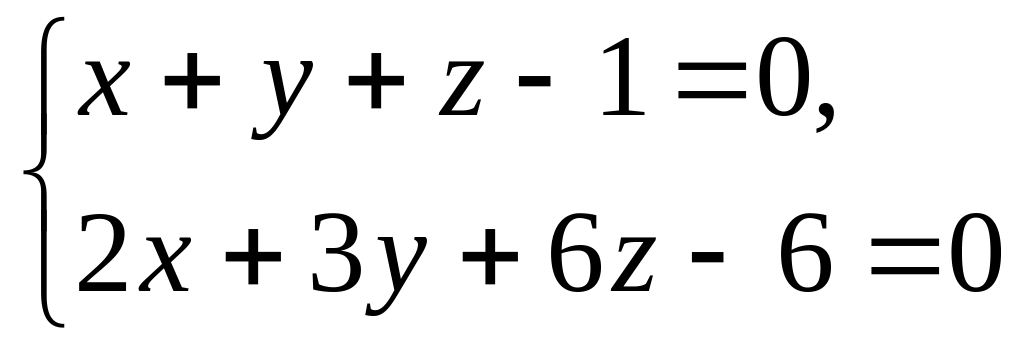 і
і
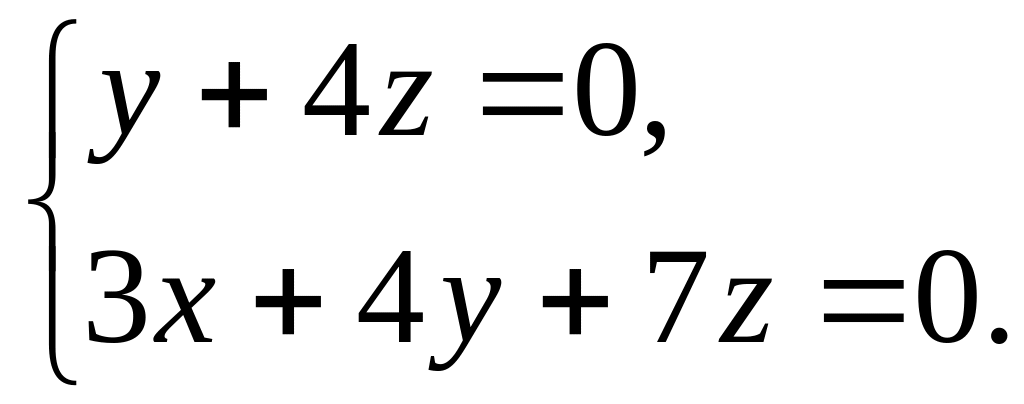
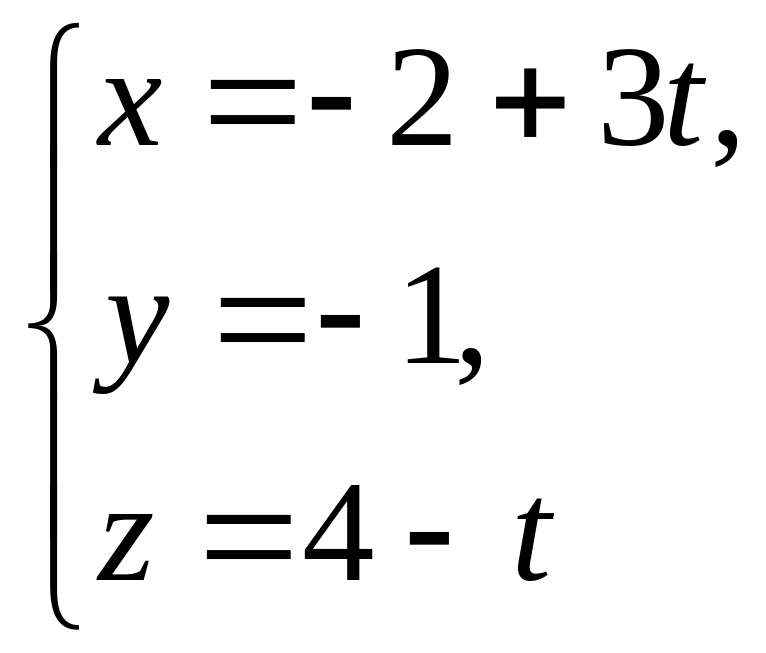 і
і
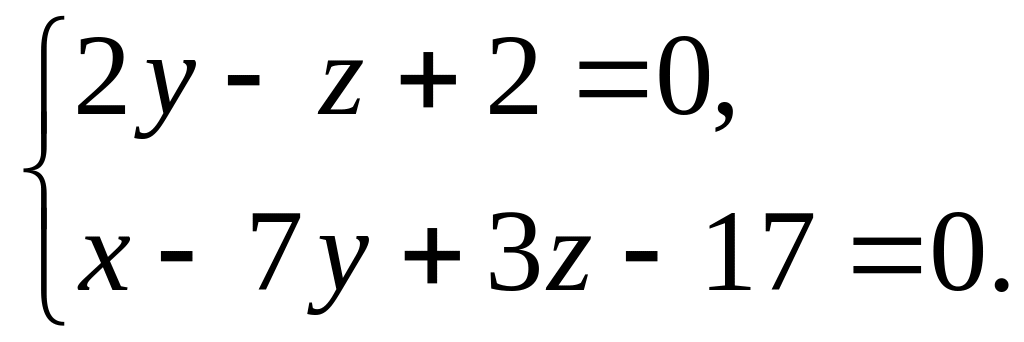
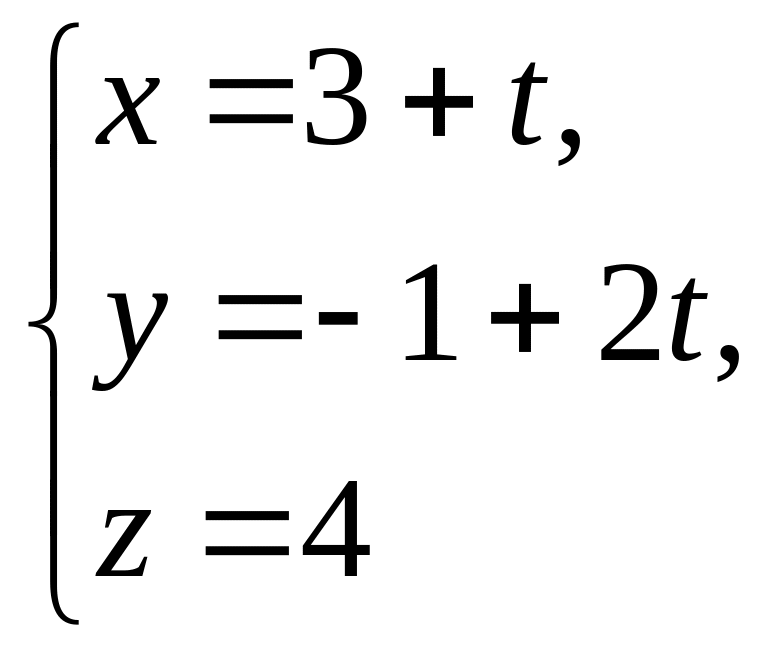 і
і
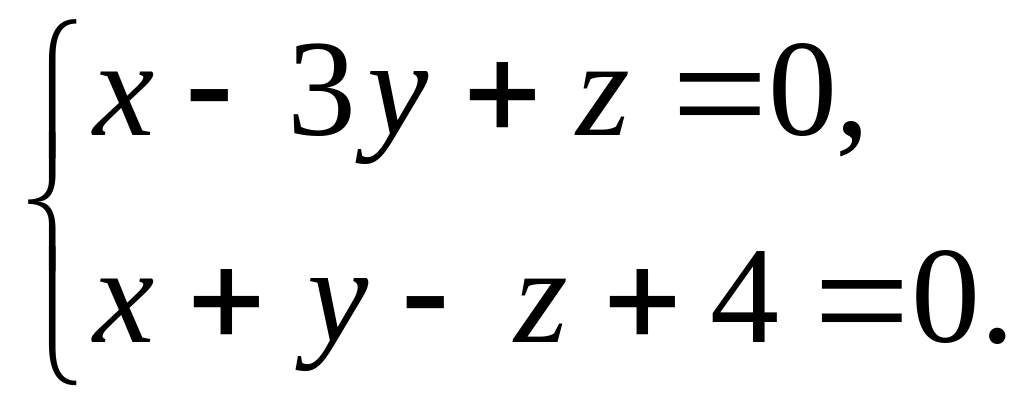
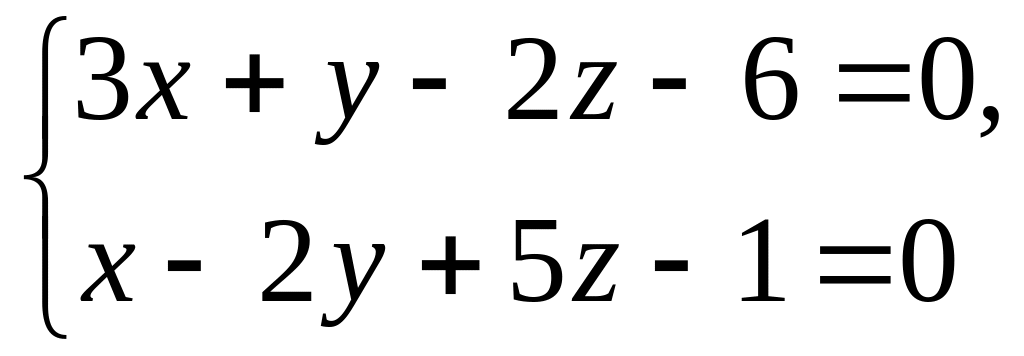 і
і
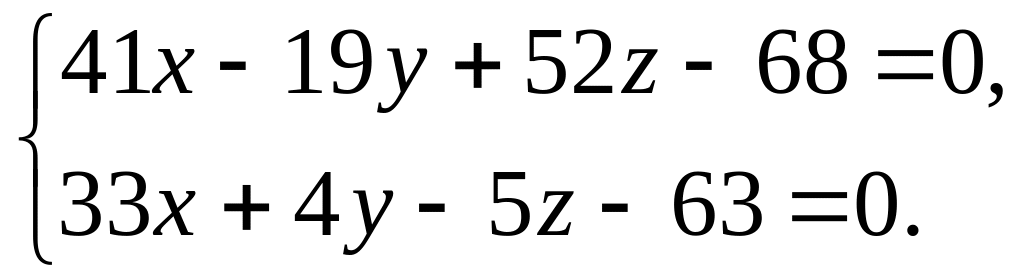
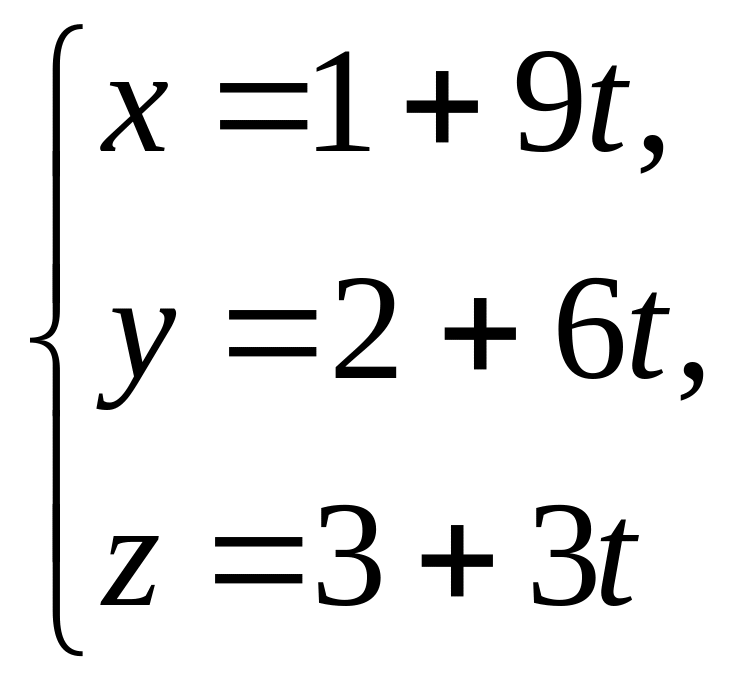 і
і
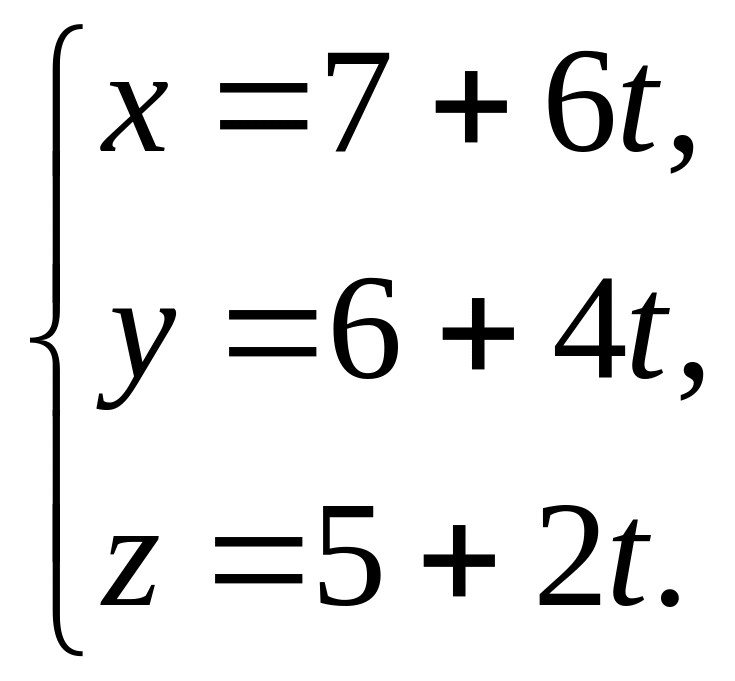
ЗАВДАННЯ № 9
Метричні задачі з теорії прямих і площин
Знайти координати точки, яка симетрична точці М(4;3;10) відносно прямої
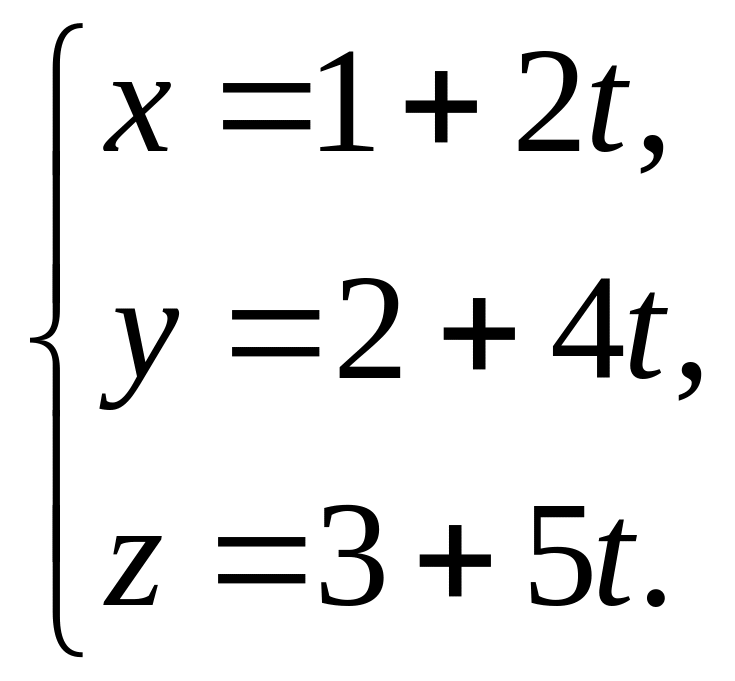
Знайти відстань між двома прямими
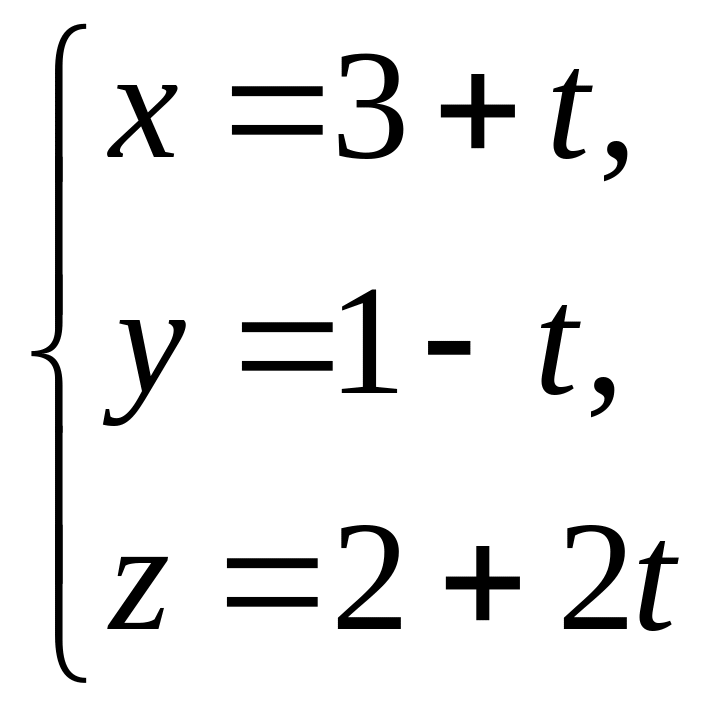 і
і
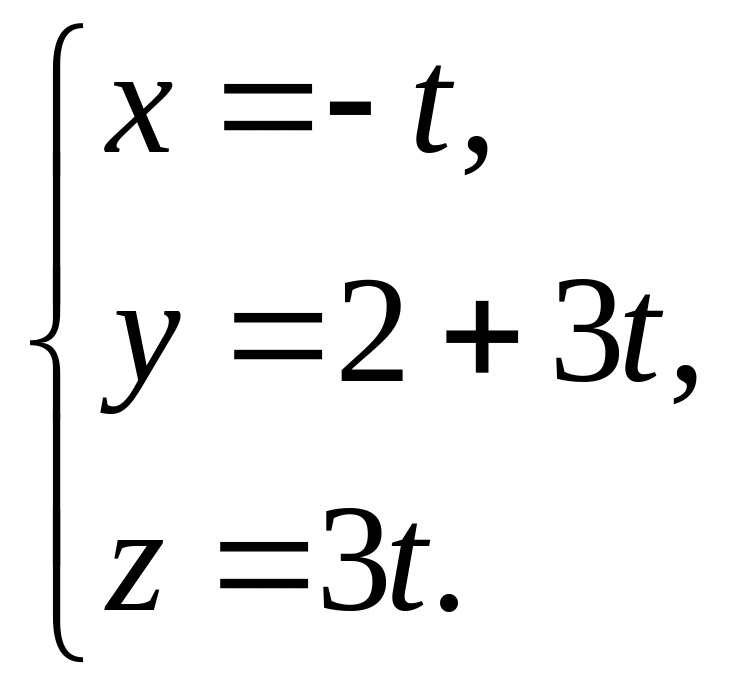
Знайти відстань між ребрами АВ та СD тетраедра АВСD, якщо А(3;-1;0), В(0;-7;3), С(-2;1;-1), D(3;2;6).
Знайти відстань між двома прямими
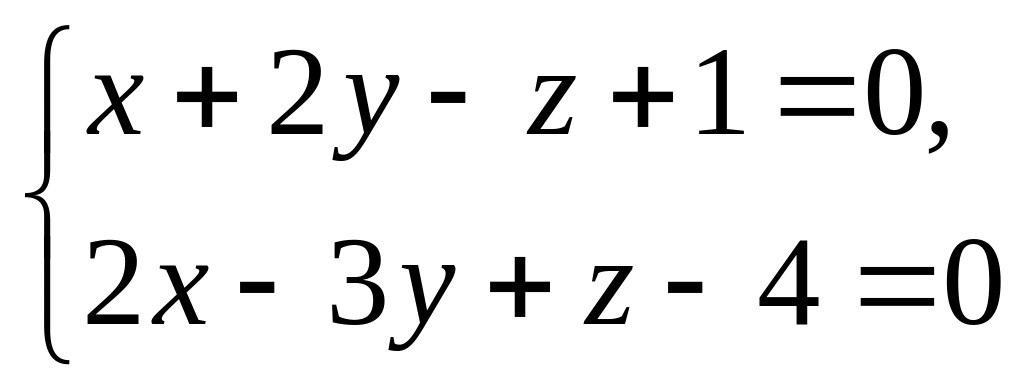 і
і
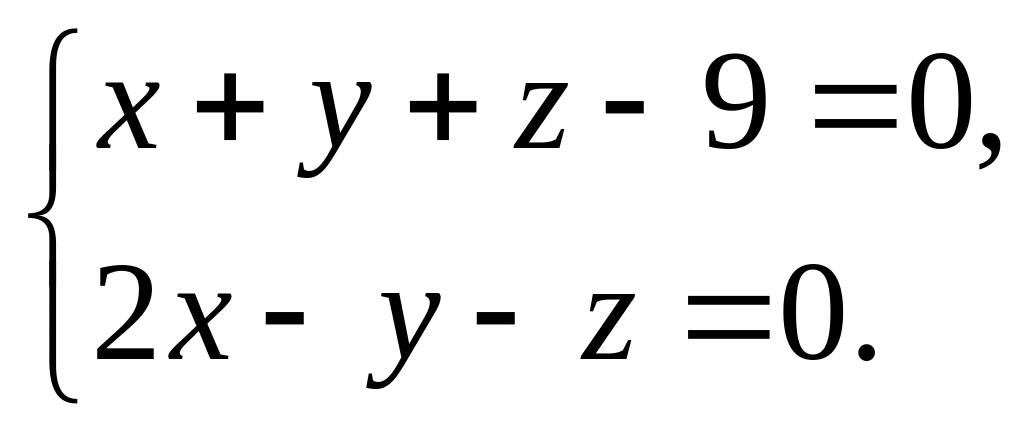
Знайти кут між ребром АВ і площиною грані ВСD тетраедра АВСD, якщо А(3;-1;0), В(0;-7;3), С(-2;1;-1), D(3;2;6).
Довести, що пряма
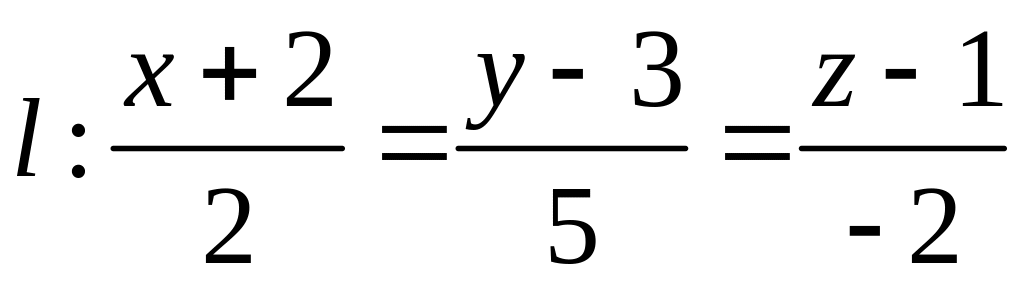 паралельна до площини
паралельна до площини
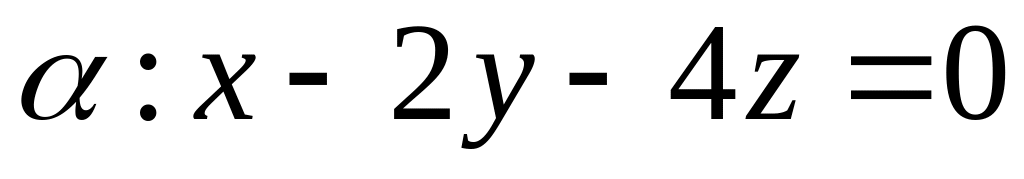 .
Знайти відстань від l
до
.
Знайти відстань від l
до
 .
.Знайти відстань між ребрами ВС та АD тетраедра АВСD, якщо А(3;-1;0), В(0;-7;3), С(-2;1;-1), D(3;2;6).
Знайти кут між ребром АС і площиною грані АВD тетраедра АВСD, якщо А(3;-1;0), В(0;-7;3), С(-2;1;-1), D(3;2;6).
Знайти відстань між двома прямими
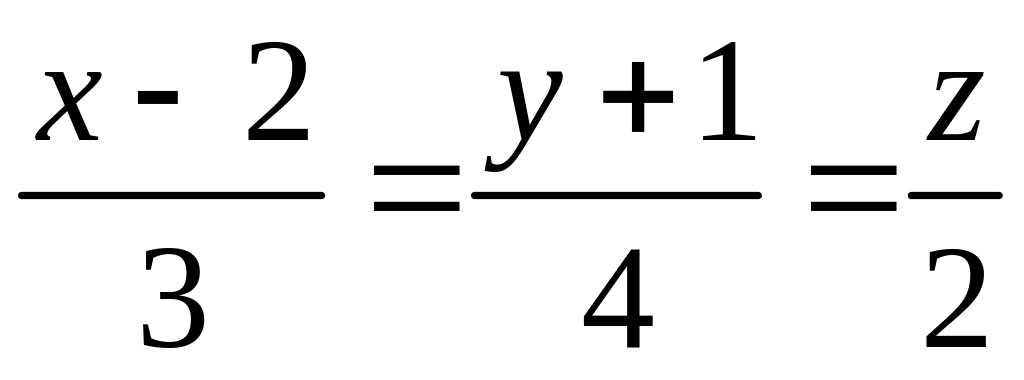 і
і
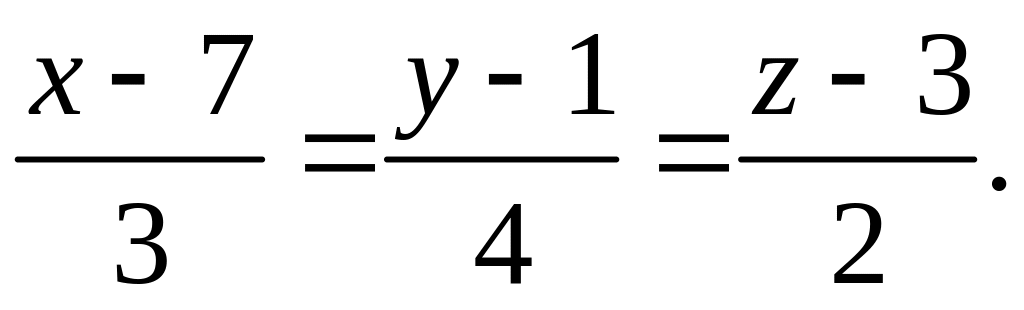
Дано трикутник : А(2;-8;6), В(0;8;3), С(3;1;6). Знайти довжину висоти трикутника, проведеної з вершини С.
Завдання № 10 Застосування теорії прямих і площин до розв’язування задач елементарної геометрії
Довести, що для висоти h трикутної піраміди зі взаємно перпендикулярними бічними ребрами, рівними a, b, c, справедлива рівність
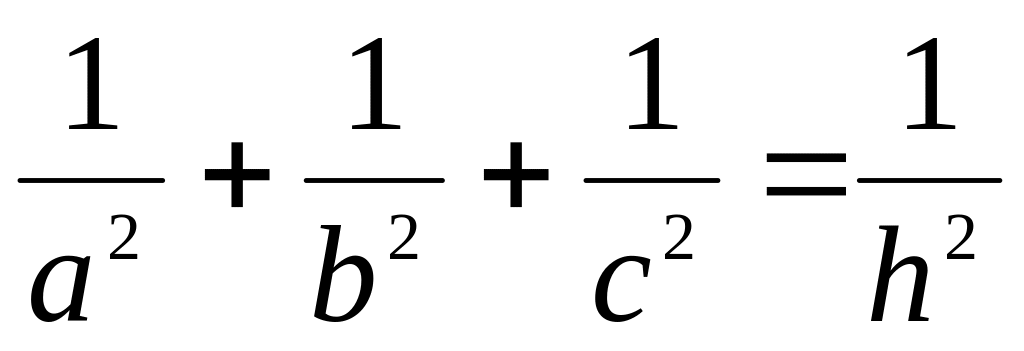 .
.У правильній чотирикутній піраміді SABCD бічна грань нахилена до площини основи під кутом . Знайти кут між площинами АКС і SAB, якщо К – середина ребра SB.
Показати, що в довільному тетраедрі шість площин, кожна з яких проходить через ребро і середину протилежного з ним ребра, перетинаються в одній точці.
У правильній трикутній піраміді SABC висота SH рівна h, сторона основи рівна а. Знайти кут між площинами АКС і HВС, де К – середина ребра SB.
Довести, що лінії перетину двох паралельних площин третьою площиною, є паралельними.
Довести, що в тетраедрі чотири прямі, що з’єднують кожну вершину з центром тяжіння протилежної грані, перетинаються в одній точці.
– правильна трикутна піраміда. Довести, що сума відстаней від будь-якої точки , яка лежить на площині до бічних граней є величина стала і не залежить від вибору точки .
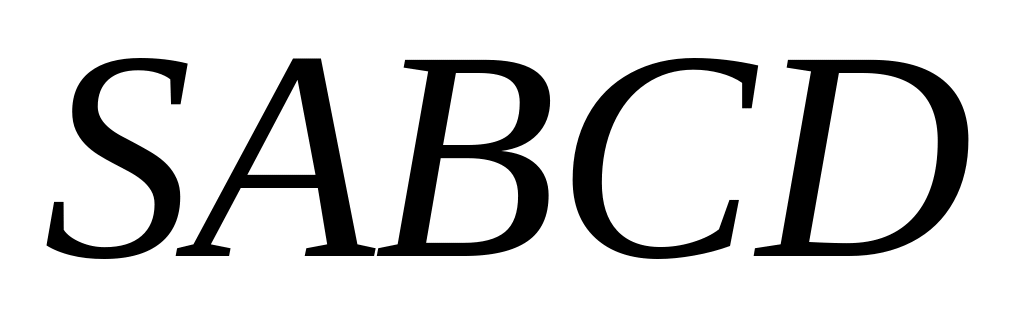 – правильна
чотирикутна піраміда. Довести, що сума
відстаней від будь-якої точки
,
яка лежить на площині
до бічних граней є величина стала і не
залежить від вибору точки
.
– правильна
чотирикутна піраміда. Довести, що сума
відстаней від будь-якої точки
,
яка лежить на площині
до бічних граней є величина стала і не
залежить від вибору точки
.Дано куб, ребро якого дорівнює
 .
Знайти відстань від вершини
.
Знайти відстань від вершини
 куба до діагоналі, що не проходить через
точку
і лежить у тому діагональному перерізі
куба, який містить цю точку.
куба до діагоналі, що не проходить через
точку
і лежить у тому діагональному перерізі
куба, який містить цю точку.Довести, що в тетраедрі три прямі, що з’єднують середини протилежних ребер, перетинаються в одній точці.
