
Мезенцев Теория систем и системный анализ / отчет мезенцев лр 1
.docxМинистерство образования и науки Российской Федерации
Федеральное агентство по образованию
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Отчёт по лабораторной работе №1
ИНСТРУМЕНТЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
БИЗНЕС-ПРОЦЕССАМИ
Выполнила:
Студентка ФБИ-22
Преподаватель:
Мезенцев Ю.А.
Новосибирск
2014
Цель. Разработка программ оптимального управления проектом с использованием средств «поиск решения» Excel.
Условия задачи:
Перед проектной фирмой стоит задача разработки календарных графиков строительства промышленного объекта для всех возможных сроков его завершения. Очередность выполнения работ, их нормальная и ускоренная продолжительность (tn, tс), стоимостные характеристики работ (Сn, Сс).
Таблица 1.
Исходные данные проекта
|
Имя |
Предш. |
tn |
tс |
Cn |
Cс |
Δ |
|
A |
E |
8 |
5 |
5 |
7 |
0,666667 |
|
B |
HEG |
22 |
12 |
12 |
22 |
1 |
|
C |
|
34 |
20 |
20 |
32 |
0,857143 |
|
D |
CFA |
30 |
20 |
20 |
30 |
1 |
|
E |
|
27 |
20 |
20 |
30 |
1,428571 |
|
F |
E |
8 |
5 |
5 |
7 |
0,666667 |
|
G |
V |
8 |
5 |
5 |
7 |
0,666667 |
|
H |
A |
8 |
5 |
5 |
7 |
0,666667 |
|
Q |
E |
38 |
20 |
20 |
40 |
1,111111 |
|
V |
|
8 |
5 |
5 |
7 |
0,666667 |
С учетом технологической последовательности работ построила сетевой график выполнения этих работ в представлении узел-операция.
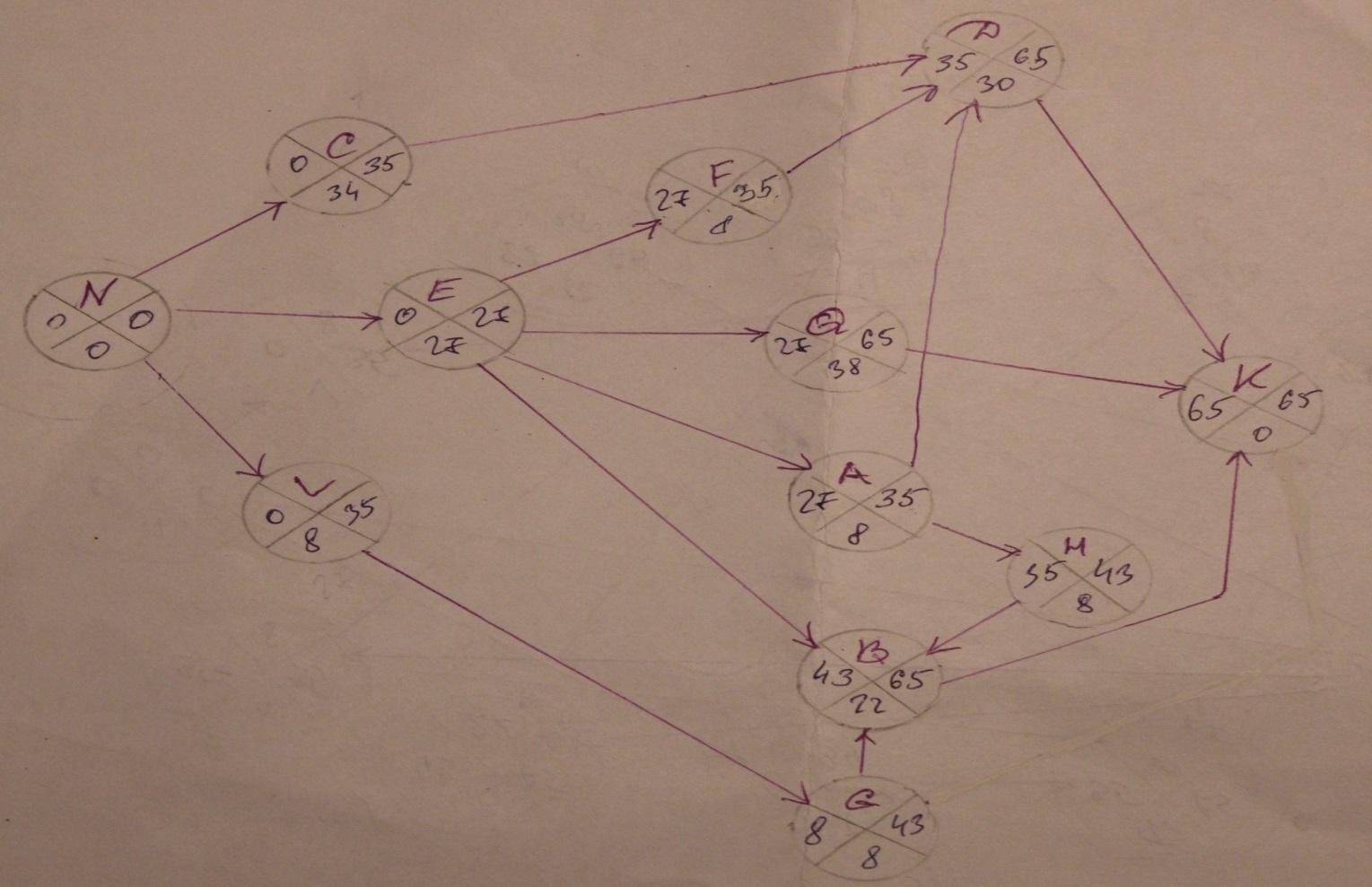
Ткр=65 дней (минимальное время, за которое мы можем выполнить весь комплекс работ)
Матрица системы ограничений и векторы коэффициентов целевых функций
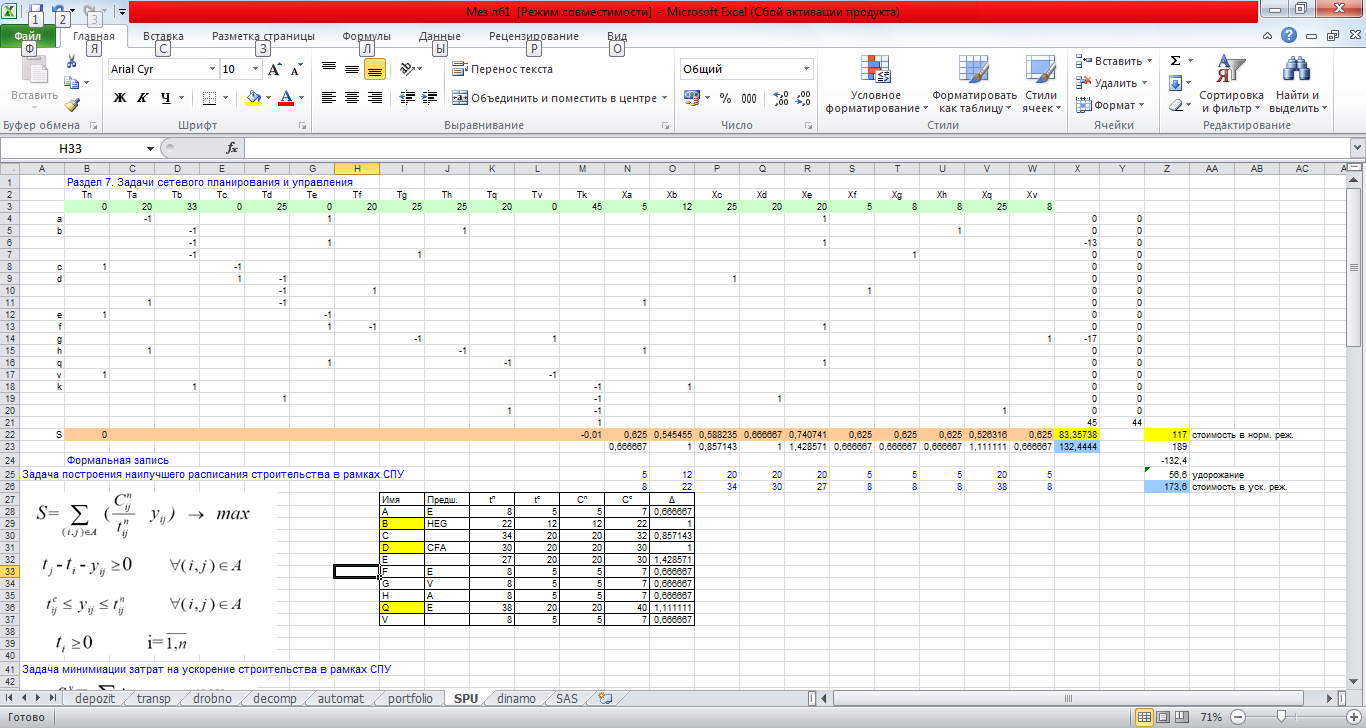
Рассчитала оптимальные по стоимости календарные графики строительства на временном интервале от 65-45 дней.
С помощью «поиск решения» рассчитала основные временные и стоимостные характеристики проекта.
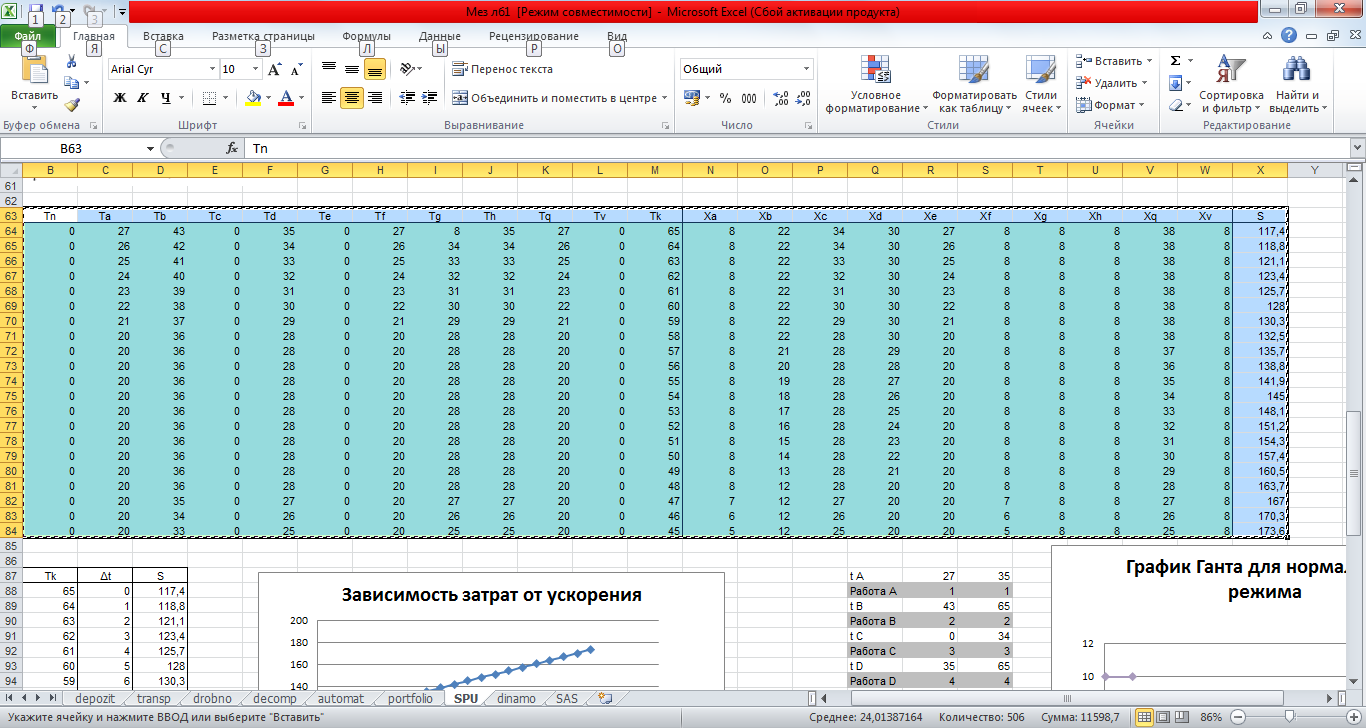
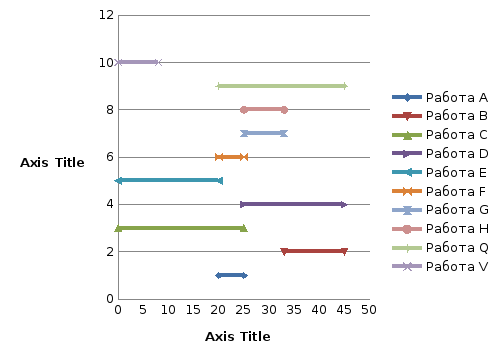
Построила диаграммы Ганта выполнения работ проекта при различных (в т.ч. нормальном и максимально интенсивном) режимах выполнения.
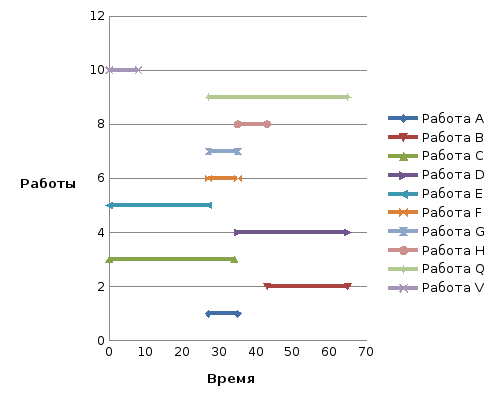
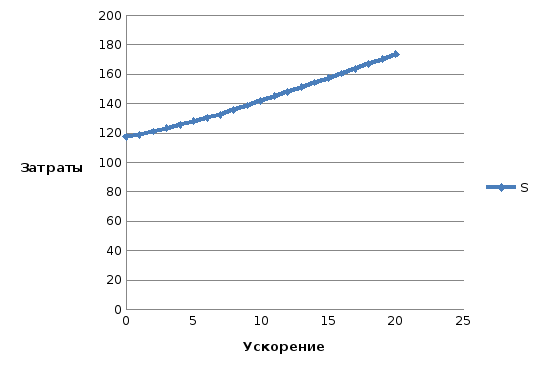
Построила диаграмму оптимальных затрат на ускорение в зависимости от сроков реализации проекта:
Решение задачи с использованием программы OPL ILOG.
// solution (optimal) with objective 116.35
T = [0 27 43 0 35 0 27 8 35 27 0
65];
x = [8 22 34 30 27 8 8 8 38 8];
// solution (optimal) with objective 112.981307189542
T = [0 24 40 0 32 0 24
8 32 24 0 62];
x = [8 22 32 30 24 8 8 8 38 8];
// solution (optimal) with objective 105.976966048514
T = [0 20 36 0 28 0 20
8 28 20 0 57];
x = [8 21 28 29 20 8 8 8 37 8];
// solution (optimal) with objective 93.8779070373498
T = [0 20 36 0 28 0 20
8 28 20 0 50];
x = [8 14 28 22 20 8 8 8 30 8];
// solution (optimal) with objective 83.357379783386
T = [0 20 33 0 25 0 20
8 25 20 0 45];
x = [5 12 25 20 20 5 8 8 25 8];
// solution (feasible relaxed sum of infeasibilities)
T = [0 20 30 5 25 0 20
5 25 25 0 45];
x = [5 12 20 20 20 5 5 5 20 5];
