2.4. Определение качества полученного уравнения регрессии и исключение незначимых факторов.

Качество уравнения характеризуют следующие показатели:

1. Коэффициент парной корреляции (r) – для однофакторных линейных моделей; коэффициент множественной корреляции (R) – для многофакторных линейных моделей; корреляционное отношение () – для нелинейных моделей.

Данные показатели изменяются в пределах –1 r 1 и 0 R()  1 и показывают силу влияния учтенных в уравнении факторных признаков на результативный. Чем ближе показатель к 1 (или –1), тем связь сильнее. Коэффициент парной корреляции, кроме этого, показывает направление связи (знак «плюс» говорит о прямой связи, знак «минус» – об обратной).

2. Коэффициент детерминации (r², R², ²), выраженный в процентах показывает, на сколько процентов учтенные в уравнении регрессии факторные признаки объясняют вариацию (влияние) результативного.

3) Критерий Фишера (F) дает общую оценку адекватности (правдивости) уравнения. Полученное значение критерия (F_расч.) сравнивают с критическим (табличным) (F_табл.) для принятого уровня значимости ( = 0,05 (приложение 13) или  = 0,01) и числа степеней свободы (₁ = m – 1 и ₂ = n – m, где n – число наблюдений, m – число факторов уравнения, включая результативный). Если оно окажется больше соответствующего табличного значения, то данное уравнение статистически значимо, т. е. доля вариации, обусловленная регрессией намного превышает случайную ошибку.

После построения уравнения регрессии возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии, что делают с помощью t-критерия Стьюдента. Расчетные значения данного показателя сравнивают с критическими, которые определяют по таблице с учетом принятого уровня значимости ( = 0,10;  = 0,05 или  = 0,01) (при изучении социально-экономических явлений достаточным считается уровень значимости, равный 0,05) и числа степеней свободы  = n – m – 1 (где n – число наблюдений; m – число факторов уравнения, включая результативный). Параметр признается значимым, если t_расч.t_табл.

Если есть коэффициент регрессии, для которого условие не выполняется, то из уравнения исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение t-критерия. После этого уравнение регрессии строится без исключенного фактора и снова проверяется значимость коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в уравнении только существенных (действительно влияющих на результативный показатель) факторов.

Иногда расчетные значения t-критерия ниже критического значения для факторных признаков, имеющих достаточно тесную связь с результативным. Это связано с проявлением эффекта мультиколлинеарности, когда два и более признака, оказывающих влияние на результативный, тесно связаны друг с другом. В таком случае включение одного из них (наиболее значимого) в уравнение регрессии позволяет учесть и влияние других.

В некоторых случаях t_расч. находится вблизи t_табл., поэтому с точки зрения содержательности уравнения такой фактор можно оставить для последующей проверки его значимости.

В рассматриваемом примере табличное значение t-критерия при уровне значимости  = 0,05 и числе степеней свободы  =27 – 3 – 1=23 равно 2,069. Расчетное значение t-критерия при факторах «среднесписочная численность работников» и «стоимость основных производственных фондов» меньше табличного значения, поэтому данные признаки исключаем из уравнения регрессии.

Выполняем опять команду СервисАнализ данных…. Выбераем инструмент анализа Регрессия и щелкните на кнопке ОК. Только теперь в качестве Х берем только «производственные затраты без амортизации».

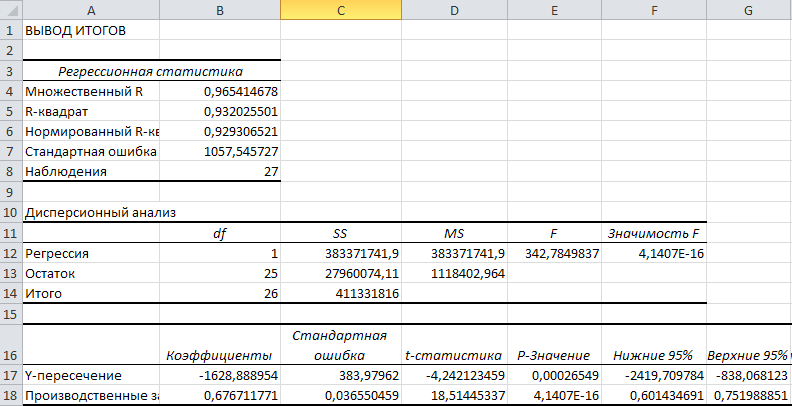
Рис. 6 Новое уравнение регрессии

После исключения незначимых факторов уравнение регрессии будет иметь следующий вид:

;

R = 0,965; R² = 0,932; F = 342,79,

где у – стоимость товарной продукции фирмы, тыс. у. е.;

х –производственные затраты без амортизации, тыс. у. е.

Факторы, включенные в уравнение регрессии оказывают сильное влияние на стоимость товарной продукции. Они объясняют вариацию (влияние) результативного показателя на 93,2% (остальные 6,8% – влияние неучтенных факторов). Расчетное значение критерия Фишера значительно превосходит табличное при значимости  = 0,01 (F_табл. = 3,05), что говорит о соответствии уравнения реальным зависимостям, проявляющимся при реализации товара.