2 Практическая часть

2.1. Определение результативных (зависимых) и факторных (независимых) признаков.

Они выбираются исходя из цели исследования, как правило, на основании логических рассуждений, учитывающих причинно-следственные связи изучаемого явления.

В нашем случае факторными признаками являются:среднесписочная численность работников, стоимость основных производственных фондов и производственные затраты без амортизации, которые оказывают влияние на стоимость товарной продукции фирмы.

2.2. Сила и направление связи между признаками.

Для того чтобы установить силуи направление связи между признаками рассчитываются коэффициенты парной корреляции (r_xy).

Данный показатель изменяется от –1 до 1. Чем ближе значения коэффициента корреляции по модулю к 1, тем сильнее связь. При этом знак «плюс» означает прямую зависимость, т. е. с увеличением одного признака другой так же увеличивается, а знак «минус» – обратную, т. е. с увеличением одного признака другой уменьшается и наоборот.

Расчета коэффициентов парной корреляции выполним в Excel.

Открываем файл, содержащий необходимые данные.

Выбираем рабочий лист с информацией, подлежащей анализу.

Выполняем команду СервисАнализ данных…. Появится диалоговое окно Анализ данных (рис. 1);

Рис. 1. Диалоговое окно «Анализ данных».

Выбераем инструмент анализа Корреляция и щелкаем на кнопке ОК. Появится диалоговое окно Корреляция (рис. 2).

В поле Входной интервал указываем диапазон ячеек, содержащий значения признаков, подлежащих изучению.

Установливаем флажок Метки в первой строке.

В поле Новый рабочий лист: указываем имя, соответствующее его содержанию (в нашем случае, Корреляция) и щелкаем на кнопке ОК. После этого создается новый рабочий лист, на который выводятся результаты расчетов.

Рис. 2. Диалоговое окно «Корреляция».

Отформатируем выведенную информацию для удобного её восприятия. В результате лист будет иметь вид представленным на рис. 3.

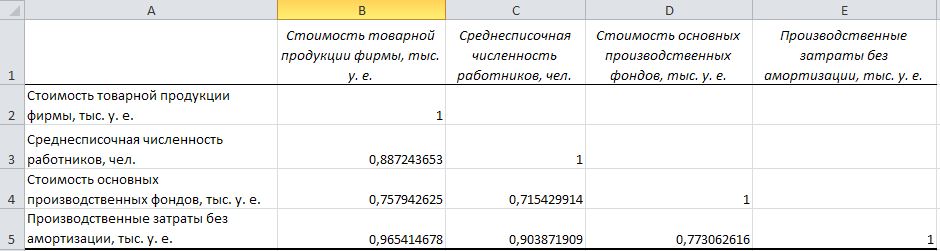
Рис. 3. Рабочий лист «Корреляция».

Коэффициенты парной корреляции показывают, что наиболее тесная связь наблюдается между стоимостью товарной продукции фирмы и производственные затраты без амортизации, причем по направлению она является прямой, т. е. с ростом произведственных затрат растет стоимость товарной продукции. Отмечается так же прямое влияние на стоимость товарной продукции фирмы среднесписачной численности работников и, в меньшей степени, стоимостью основных производственных фондов.

2.3. Определение вида уравнения регрессии и расчет его параметры.

Зачастую возникает необходимость не только выявить наличие и силу связи, но и установить, каким будет значение результативного признака при известном значении факторного. Для этого необходимо построить уравнение регрессии.

Различают следующие виды уравнений регрессии: по форме связи – линейные и нелинейные; по числу факторных показателей – однофакторные и многофакторные.

Если зависимый признак определяется влиянием только одного независимого, то используется однофакторное уравнение регрессии.

В случае линейной зависимости между признаками применяется линейная математическая функция .

Для описания нелинейной зависимости Excel позволяет использовать следующие математические функции:

логарифмическую: ;

степенную: ;

экспоненциальную: ;

полиномиальную: .

Выбрать функцию, наилучшим образом описывающую взаимосвязь между факторными и результативным признаками, можно следующими способами:

1) логическим (уравнение выбирается на основании логического анализа и имеющегося опыта);

2) графическим (по фактическим данным строится поле корреляции между факторным и результативным признаками, на основании которого подбирается математическая функция);

3) аналитическим (строится несколько уравнений регрессии с использованием различных математических функций, среди которых выбирается лучшее на основании показателей, которые будут рассмотрены ниже).

Выполним построение уравнения регрессии в Excel.

Построим поле корреляции (рис. 4).

С помощью команды ДиаграммаДобавить линию тренда… построим различные линии тренда.

При изучении влияния производственных затрат на стоимость товарной продукции были получены следующие уравнения регрессии:

линейное: , R² = 0,932;

логарифмическое: , R² = 0,7029;

степенное: , R² = 0,9023;

экспоненциальное: , R²= 0,7991;

полиномиальное (парабола): , R²= 0,9629.

Рис. 4 Поле корреляции

Показателем, характеризующим в данном случае качество полученных уравнений регрессии является коэффициент детерминации. Сравнивая их, можно сделать вывод, что наилучшим образом описывает влияние производственных затрат на стоимость товарной продукции уравнение параболы. Однако почти не уступает ему линия тренда, выраженная прямой линией.

В том случае, когда существует несколько факторов, оказывающих влияние на результативный показатель, для описания зависимости используется линейное многофакторное уравнение регрессии (построить нелинейное многофакторное уравнение непосредственно невозможно, его необходимо сначала привести к линейной форме), которое имеет следующий вид:

Построим линейное уравнение регрессии (как однофакторного, так и многофакторного) в Excel.

Выполним команду СервисАнализ данных…. Выбираем инструмент анализа Регрессия и щелкните на кнопке ОК.

В поле Входной интервал Y: указываем диапазон ячеек, содержащий значения результативного (зависимого) признака. В поле Входной интервал Х: указываем диапазон ячеек, содержащий значения факторных (независимых) признаков. В поле Новый рабочий лист: введём имя, соответствующее его содержанию (в нашем случае, Регрессия) и щелкаем на кнопке ОК. После этого в рабочую книгу добавляется новый рабочий лист, содержащий уравнение регрессии и его характеристики (рис. 5).

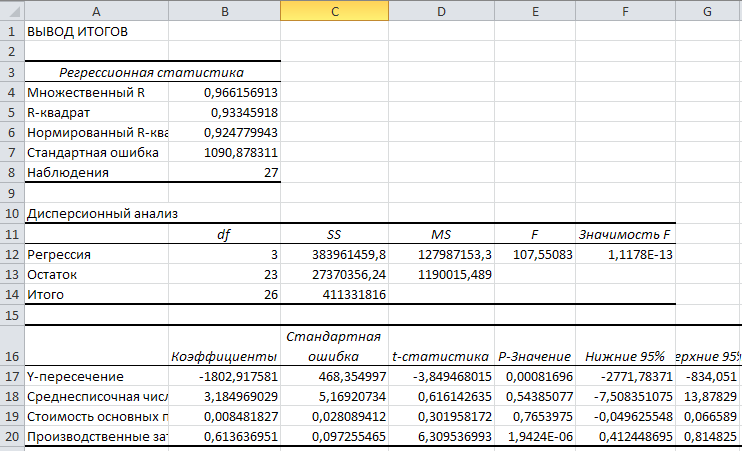
Рис. 5 Характеристики уравнения регрессии

Уравнение регрессии имеет следующий вид: