Лабораторная работа №1 Интерполирование функций в MathCad
Цель работы: изучить некоторые возможности аппроксимации опытных данных, которые предоставляются программной средой MathCAD; получить представление об интерполировании функций как классическом методе аппроксимации; осуществить сравнительный анализ различных способов интерполяции и научиться оценивать погрешность многочленной интерполяции.
Интерполяция
Для построения
интерполяции-экстраполяции в MathCAD
имеются несколько встроенных функций,
позволяющих "соединить" точки
выборки данных
кривой разной степени гладкости. По
определению, интерполяция означает
построение функции
,
аппроксимирующей зависимость
в промежуточных точках отрезка
.
Поэтому интерполяция есть один из
методов аппроксимации. В точках
значения интерполяционной функции
должны совпадать с исходными данными,
т. е.
.
Примечание.
Будем использовать вместо обозначения
другое
имя ее аргумента
,
чтобы не путать вектор данных
и скалярную переменную
.
Линейная интерполяция
Самый простой вид интерполяции - линейная, которая представляет искомую зависимость в виде ломаной линии. Интерполирующая функция состоит из отрезков прямых, соединяющих точки (рис. 1).
Для построения линейной интерполяции служит встроенная функция linterp.
- linterp (
,
,
)
- функция, аппроксимирующая данные
векторов
и
кусочно-линейной зависимостью;
- вектор действительных данных аргумента;
- вектор действительных данных значений того же размера;
- значение аргумента, при котором вычисляется интерполирующая функция.
Элементы вектора
должны быть определены в порядке
возрастания, т. е.
.
Пример 1. Линейная интерполяция (рис. 1)
Рис. 1. Линейная интерполяция (пример 1)
Как видно из примера 1, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
1) Введите векторы данных и (первые две строки примера 1).
2) Определите функцию linterp ( , , ).
3) Вычислите значения этой функции в требуемых точках, например linterp( , ,2.4)=3.52, или linterp(х, ,6) =5.9, или постройте ее график, как показано на рис. 1.
Примечание. Обратите внимание, что функция на графике имеет аргумент , а не . Это означает, что функция вычисляется не только при значениях аргумента (т.е. в семи точках), а при гораздо большем числе аргументов в интервале (0,6), что автоматически обеспечивает MathCAD. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции от векторного аргумента MathCAD, по умолчанию, соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
Сплайн-интерполяция
Сплайн — это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.
В большинстве
практических приложений желательно
соединить экспериментальные точки не
ломаной линией, а гладкой кривой. Лучше
всего для этих целей подходит интерполяция
кубическими сплайнами, т. е. отрезками
кубических парабол. Смысл кубической
сплайн-интерполяции заключается в том,
что в промежутках между точками
осуществляется аппроксимация в виде
зависимости
.
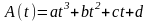Коэффициенты a, b, c, d рассчитываются
независимо для каждого промежутка,
исходя из значений
в соседних точках. Этот процесс скрыт
от пользователя, поскольку смысл задачи
интерполяции состоит в выдаче значения
в любой точке t (рис.2).
- interp(s, , , ) - функция, аппроксимирующая данные векторов и кубическими сплайнами;
s - вектор вторых производных, созданный одной из сопутствующих функций
cspline, pspline или lspline;
- вектор действительных данных аргумента, элементы которого расположены в
порядке возрастания;
- вектор действительных данных значений того же размера;
- значение аргумента, при котором вычисляется интерполирующая функция.
Пример 2. Кубическая сплайн-интерполяция (рис.2)
Рис.2. Кубическая сплайн-интерполяция (пример 2)
Рис.3. Примеры сплайн-интерполяций
Сплайн-интерполяция
в MathCAD реализована чуть сложнее линейной.
Перед применением функции interp необходимо
предварительно определить первый из
ее аргументов - векторную переменную
s. Делается это при помощи одной из трех
встроенных функций тех же аргументов
.
- lspline( , ) - вектор значений коэффициентов линейного сплайна;
- pspline( , ) -вектор значений коэффициентов квадратичного сплайна;
- cspline( , ) – вектор значений коэффициентов кубического сплайна;
- , - векторы данных.