10 Пример расчета сложной цепи

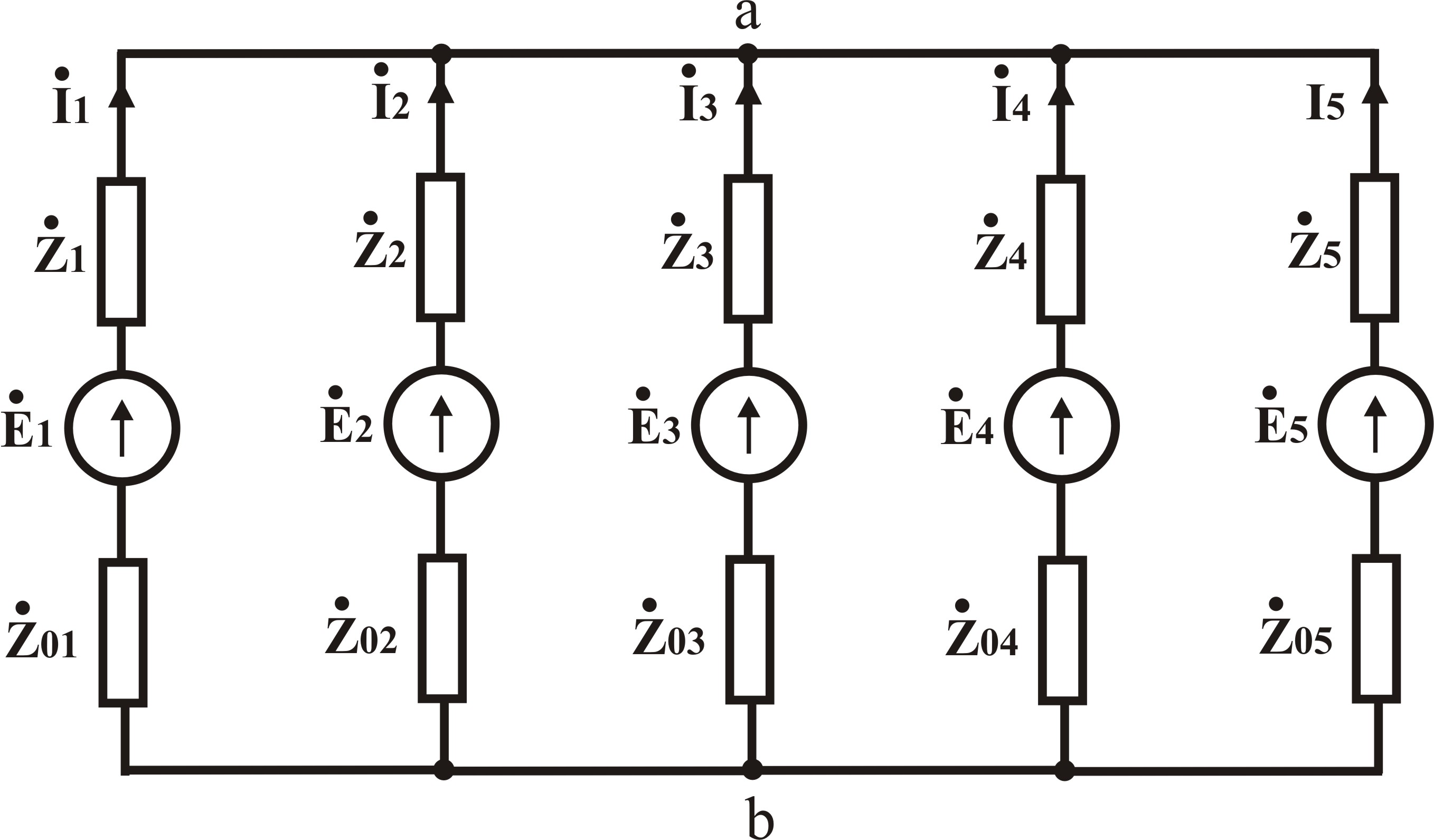
Рис.1 Полная схема цепи

Задание для расчета:

1. В соответствии с заданием изменить схему Рис.1 , разомкнув в ней соответствующие ветви и исключив отсутствующие источники ЭДС и сопротивления.

2. Найти токи всех ветвей методом непосредственного применения законов Кирхгофа

3. Составить уравнение баланса мощностей и проверить полученные результаты

4. Найти токи всех ветвей методом контурных токов и сравнить результаты расчета с полученными ранее.

5. Найти токи всех ветвей методом наложения и проверить полученные результаты по I-ому закону Кирхгофа.

6. Найти токи всех ветвей методом узловых напряжений.

7. Найти токи всех ветвей методом эквивалентного генератора.

Начальные данные для расчета.

Цепь для рассматриваемого примера(рис.2) содержит ветви со следующими параметрами (ЭДС – В, сопротивления – Ом):

E₁ = 100 + j0 = 100 ; Z₀₁ = 2 – j3; Z₁ = 2 + j6;

E₂ = 0 + j100 = 100 ; Z₀₂ = 2 – j2; Z₂ = 6 - j4;

E₃ = 0 + j0 = 0; Z₀₃ = 0 + j0; Z₃ = 8 + j6;

E₄ = 60 – j80 = 100 ; Z₀₄ = 0 – j2; Z₄ = 0 + j12;

5-я ветвь разомкнута

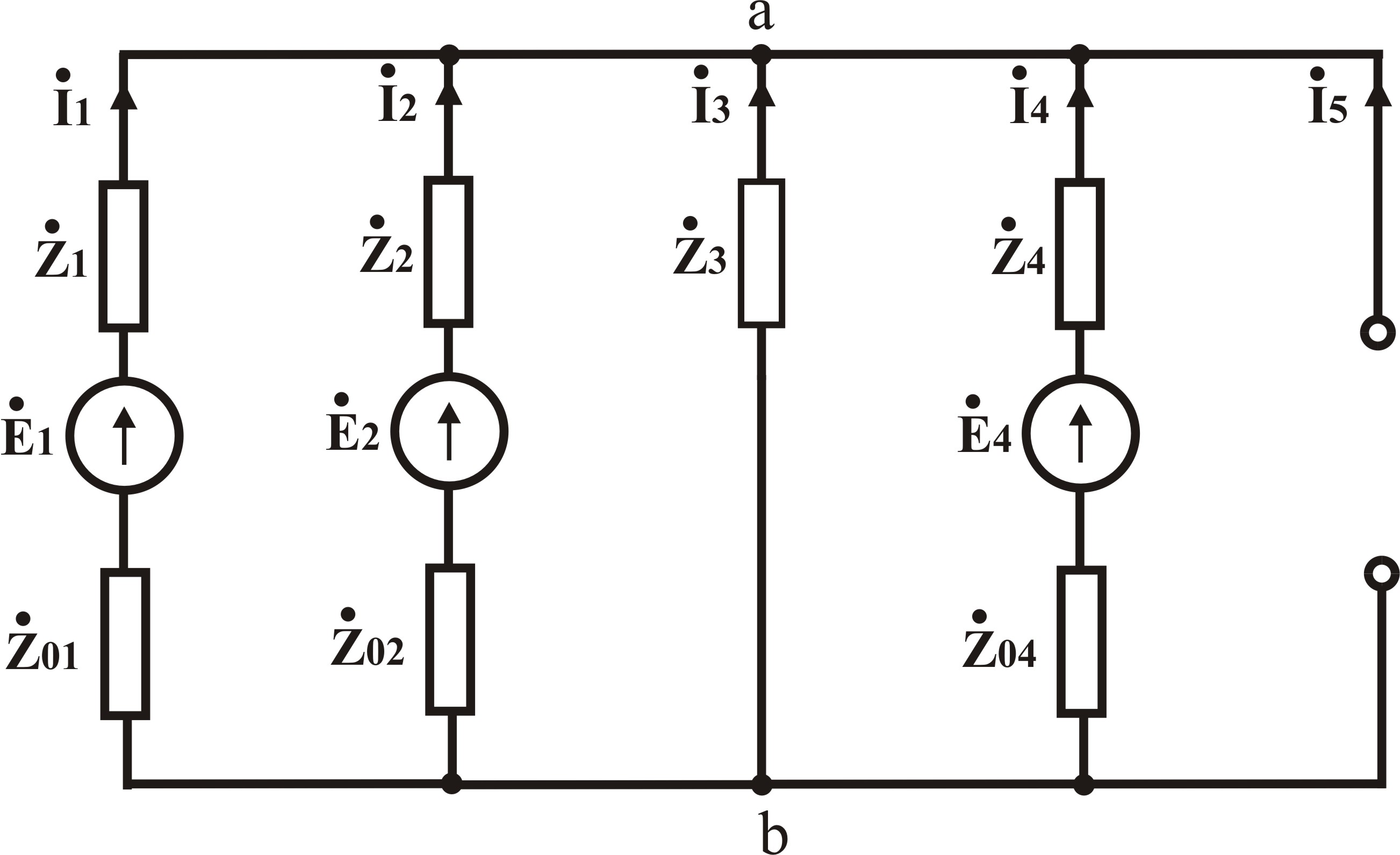
Рис.2 Схема рассматриваемого примера

Для упрощения расчетных выражений определим суммарное сопротивление каждой ветви

Z₁₁ = Z₁+Z₀₁ = 4 + j3 = 5e ^j36,870

Z₂₂ = Z₂+Z₀₂ = 8 – j6 = 10e ^-j36,870

Z₃₃ = Z₃+Z₀₃ = 8 + j6 = 10e ^j36,870

Z₄₄ = Z₄+Z₀₄ = 0 + j10 = 10e ^j90

1. Расчет цепи методом непосредственного применения законов Кирхгофа

Для определения 4-х неизвестных токов нужно составить 4 независимых уравнения.

Произвольно выбираем направления токов. В схеме (рис.2) 2 узла, поэтому по I закону Кирхгофа можно написать только 1 уравнение

I₁+I₂+I₃+I₄ =0 (1.1)

Недостающие 3 уравнения нужно написать по II закону Кирхгофа

Уравнение для контура I Z₁₁I₁ –Z₂₂I₂ = E₁ – E₂ (1.2)

Уравнение для контура II Z₂₂I₂ –Z₃₃I₃ = E₂ – E₃ (1.3)

Уравнение для контура III Z₃₃I₃ –Z₄₄I₄ = E₃ – E₄ (1.4)

Из уравнения 1.1 I₄ = – I₁ – I₂ – I₃

Заменив I₄ в уравнении 1.4, получим следующее уравнение для контура III

Z₄₄I₁ + Z₄₄I₂ + (Z₃₃ + Z₄₄) I₃ = E₃ – E₄ (1.5)

Систему трех уравнений (1.2, 1.3, 1.5) можно привести к стандартному виду

a₁₁I₁ + a₁₂I₂ + a₁₃I₃ = E₀₁

a₂₁I₁ + a₂₂I₂ + a₂₃I₃ = E₀₂ (1.6)

a₃₁I₁ + a₃₂I₂ + a₃₃I₃ = E₀₃

где:

a₁₁ = Z₁₁ = 4 + j3 = 5e ^j36,870;

a₁₂ = -Z₂₂ = -8 + j6 = 10e ^j143,130

a₁₃ = 0;

a₂₁ = 0;

a₂₂ = Z₂₂ = 8-j6 = 10e ^-j36,870;

a₂₃ = -Z₃₃= -8-j6 = 10e ^–j143,130

a₃₁ = Z₄₄ = 0 + j10 = 10e ^j90

a₃₂ = Z₄₄ = 0 + j10 = 10e ^j90

a₃₃ = (Z₃₃+Z₄₄) = 8 + j16 = 17.888e ^j63.435

E₀₁ = E₁ – E₂ = 100-j100 = 141.421e ^–j45

E₀₂ = E₂ – E₃ = j100 = 100e ^j90

E₀₃ = E₃ – E₄ = -60+j80 = 100e ^j126.870

Главный определитель системы трех уравнений можно вычислить следующим образом

=

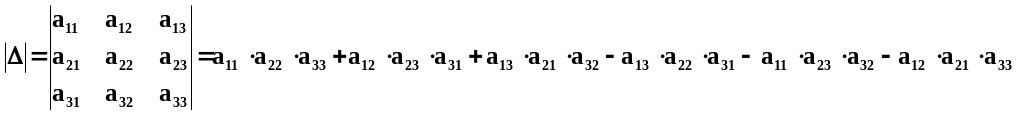= -80 +j1940 =1940e ^j92,361

Первый частный определитель

=

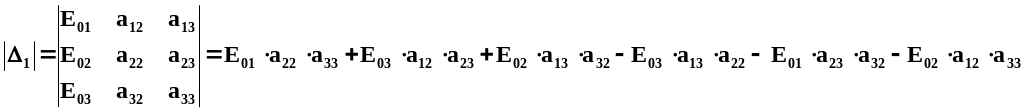= 12000 + j30000 = 32311e ^j68,199

Второй частный определитель

=

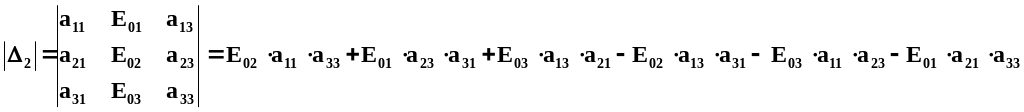= -15480 - j17360 = 23259e^-j131,724

Третий частный определитель

=

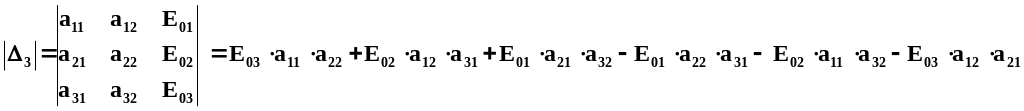= -5000 - j1000 = 5099.0e ^j-168,69

Ток первой ветви = 16,641 e ^–j24,163 = 15.183 - j6.812 (А)

Ток второй ветви = 11,979 e ^j135,92 = -8.605 + j8.334 (А)

Ток третьей ветви = 2,6262 e ^j98,948 = -0.408 + 2.594 (А)

Ток четвертой ветви находим из уравнения 1.1

I₄ = – I₁ – I₂ – I₃ = -6,170 - j4.117 = 7.417 e ^j-146.29 (А)

Ток пятой ветви I₅ = 0 (ветвь разомкнута)