2 Приведение симметричной матрицы к диагональному виду
2.1 Скалярное произведение в пространстве Rn. Процесс ортогонализации
В юните 1 нашего курса уже было введено понятие скалярного произведения в пространстве Rn. Напомним его.
Пусть
и
– два вектора пространства Rn,
тогда скалярным
произведением
векторов
и
называется число
:
,
или
.
В следующих главах будет обобщено понятие скалярного произведения и рассмотрены его основные свойства.
Здесь напомним, что длина вектора (норма вектора)
.
Два
вектора
и
ортогональны,
если их скалярное произведение равно
нулю, т.е.
.
Определение.
Система векторов
,
в Rn
ортогональна,
если
1.
,
для всех
;
2.
,
для всех
.
Можно доказать (что будет сделано ниже), что ортогональная система линейно независима.
Определение. Ортонормированной называется система векторов , из Rn, если
1) система ортогональна;
2)
длина каждого вектора системы равна 1,
т.е.
,
.
Любой
вектор
можно нормировать,
т.е. построить такой вектор
,
что
.
Вектор называется ортом вектора , если его длина равна единице, а его координаты:
.
Например,
ортом вектора
является
вектор
,
т.к.
.
Итак, всякую ортогональную систему легко превратить в ортонормированную.
Любая ортонормированная система из n векторов пространства образует ортонормированный базис пространства .
Пусть
линейно независимая система векторов
из
.
Тогда ее можно ортого-нализовать,
т.е. построить ортогональную систему
векторов
такую что, линейные оболочки векторов
и
совпадают
.
О линейной оболочке см. юниту 1.
Покажем, как из системы строится система .
Алгоритм
процесса
ортогонализации:
1)
,
2)
,
коэффициент
подберем так, чтобы
и
были ортогональны, т.е.
.
,
отсюда
.
3.
,
1
и
2
находим из условий:
и
,
или
,
т.к.
,
то
.
,
т.к.
,
то
.
Итак,
,
или
.
Аналогично строятся векторы , где
.
Заметим,
что векторы новой системы
являются линейными комбинациями векторов
линейно независимой системы
,
т.е. принадлежат
.
Итак,
от произвольного базиса
линейной
оболочки
мы перешли к ортогональному базису
,
причем
.
Пример.
В пространстве
векторы
и
не коллинеарные и образуют базис. Т.к.
,
то базис
не ортогональный. Построим ортогональный
базис
.
1.
.
2.
,
где
,
(рисунок
4).
Рисунок 4
Базис – ортогональный, но не нормированный. Нормируем этот базис:
;
,
;
.
Базис
– ортонормированный стандартный базис.
Стандартные
базисы
в
и
,
,...,
в
являются ортонормированными базисами.
2.2 Ортогональная матрица
Пусть
– базис в
пространстве
,
а
– другой
базис того же пространства. Векторы
однозначно выражаются через базис
:
или
.
Запишем
координаты вектора
по базису
в k-ый
столбец матрицы А:
.
Напомним,
что эта матрица называется матрицей
перехода от базиса
к базису
.
Матрица А
невырождена, т.к. ее столбцы – координаты
базисных векторов
,
следовательно существует обратная
матрица
,
которая является матрицей перехода от
базиса
к базису
.
Рассмотрим
частный случай, когда
и
– два
ортонормированных базиса в
и
.
Обозначим матрицу перехода U,
.
Матрица
U
обладает следующими свойствами: ее
вектор – столбцы
образуют ортонормированный базис в
,
т.е.
а)
,
б)
.
Определение.
Квадратная матрица порядка n,
столбцы которой удовлетворяют условиям
,
называется ортогональной.
Перечислим основные свойства ортогональной матрицы U:
1. Строки матрицы U (как и ее столбцы) образуют ортонормированный базис в .
2.
,
т.е. вычисление обратной матрицы для U
сводится к ее транспонированию.
3.
для всех
.
Это свойство означает, что скалярное произведение при действии ортогональной матрицы U на векторы сохраняется, а значит сохраняются длины векторов и углы между ними.
Любое из перечисленных свойств может служить определением ортогональной матрицы. Мы будем придерживаться первоначально данного определения.
Рассмотрим примеры.
1.
В пространстве
поворот на угол
по часовой стрелке задается матрицей
перехода
.
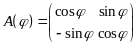Легко
проверить, что матрица
ортогональна. Из геометрических
соображений очевид-но, что длины векторов
и углы между ними при таком преобразовании
сохраняются.
2. В пространстве рассмотрим преобразование – отражение вектора относительно оси ОХ (рисунок 5).
Рисунок 5
При
таком преобразовании базис
перейдет в базис
,
.
Тогда, матрица перехода А
от базиса
к базису
имеет вид:
.
Очевидно, это преобразование сохраняет длины векторов и углы между ними, а матрица перехода А ортогональна.
В заключение посмотрим, как меняются координаты вектора при переходе от одного базиса к другому.
Пусть
в
заданы два
базиса
и
.
Обозначим С
матрицу перехода от старого базиса
к новому
базису
,
т.е.
,
.
Выберем произвольный вектор
,
разложим его по “старому” базису :
.
Аналогично, разложение этого вектора по “новому” базису имеет вид:
.
Зависимость
между “старыми” координатами
и “новыми”
вытекает из следующей цепочки равенств:
.
Так как разложение вектора по базису единственно, то получаем
,
.
(*)
Обозначим вектора – столбцы старых и новых координат соответственно
и
,
,
тогда равенство (*) можно записать так:
.
(**)
Итак,
чтобы получить координаты вектора в
“старом” базисе необходимо его вектор
– столбец “новых” координат умножить
слева на матрицу перехода из старого
базиса в новый. Так как матрица С
имеет обратную
,
то умножив равенство (**) слева на матрицу
,
получим выражение “новых” координат
через “старые”:
.
Пример.
“Старый” базис в пространстве
(на плоскости) –
“новый” базис
получен из “старого” поворотом на угол
по часовой стрелке (рисунок 6, 7). Матрица
перехода от базиса
к базису
.
Пусть
вектор
в базисе
имеет
координаты
.
Найдем координаты
в базисе
(рисунок 6, 7).
,
,
т.е.
,
.
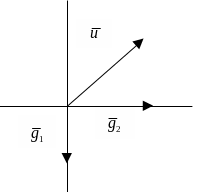
Рисунок 6 Рисунок 7