1.2 Характеристический многочлен

Пусть – собственное число матрицы А. Тогда существует вектор , что .

Перепишем это равенство в виде

. (*)

Последнее векторное равенство является системой линейных однородных уравнений. Такая система всегда имеет нулевое решение. Напомним, что для того чтобы вектор , удовлетворяю-щий этой системе, был собственным, нужно, чтобы система (*) имела ненулевое (и, следова-тельно, не единственное) решение. Тогда ее, определитель

. (**)

Обратно, если определитель однородной системы (*) равен нулю, то эта система имеет нену-левое решение, т.е. существует собственный вектор , отвечающий данному .

Итак, имеет место теорема. Для того, чтобы было собственным числом матрицы А, необходимо и достаточно, чтобы

.

Рассмотрим равенство (**) подробнее.

Матрица имеет вид:

.

Следовательно, равенство (**) можно записать так:

.

Левая часть этого равенства является многочленом степени n относительно , обозначим его .

Многочлен называется характеристическим многочленом матрицы А, а уравнение (**) называется характеристическим уравнением. Напомним, что число есть корень многочлена , если .

Тогда, последнюю теорему можно сформулировать так.

Теорема. Число – собственное число матрицы А тогда и только тогда, когда – корень характеристического многочлена этой матрицы.

Известно, что многочлен степени n имеет ровно n корней (с учетом их кратности) действительных или комплексных. Нас будут интересовать только действительные собственные числа и отвечающие им собственные векторы.

Рассмотрим пример: найти собственные значения и собственные векторы матрицы

; ,

; , .

Соответствующие собственные векторы , .

Такие собственные числа и векторы мы не будем рассматривать.

Итак, наша задача состоит в отыскании вещественных корней характеристического многочлена.

В дальнейшем, говоря о собственных числах, мы будем иметь в виду лишь вещественные собственные числа.

Пример 1. Найти собственные числа матрицы

.

Характеристический многочлен имеет вид:

.

Характеристическое уравнение:

или .

Корни характеристического многочлена: , – собственные числа матрицы А.

Пример 2. Найти собственные числа матрицы

.

Характеристический многочлен:

.

Разложим определитель по первой строке:

.

Характеристическое уравнение:

или .

Корни характеристического многочлена: , . Многочлен имеет два различных корня 3, 6, причем корень 3 кратности 2.

1.3 Собственное подпространство

Пусть  – собственное число матрицы А. Как найти собственные векторы, отвечающие данному ? Как говорилось, следует данное значение  подставить в уравнение (*) и найти все решения этой системы:

. (***)

Определитель этой однородной системы равен нулю, все решения такой системы образуют подпространство пространства Rⁿ (см. юниту 1), ненулевые векторы которого составляют собст-венное подпространство V_, собственных векторов, отвечающих данному значению .

Строго говоря, V_ не является подпространством, т.к. не содержит 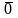-вектора. Но, когда говорят о собственном подпространстве V_, то вектор добавляется ко всем собственным.

Чтобы найти общее решение системы (***), следует найти фундаментальную систему реше-ний (ФСР), образующую базис V_. Напомним, что размерность подпространства решений равна , где n – число переменных, r – ранг матрицы (А–Е) при данном .

.

Справедлива теорема.

Теорема. Размерность собственного подпространства V_ не превосходит кратности  характеристического многочлена .

.

Найдем собственные векторы матриц в рассмотренных ранее примерах.

Матрица

имеет собственные числа , . Пусть , тогда система примет вид:

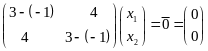, или .

Система эквивалентна одному уравнению , здесь n=2, r=1, x₂ – свободная переменная, х₁ – зависимая. ФСР состоит из одного вектора , который образует базис в одномерном собственном подпространстве .

Пусть теперь , тогда для собственного вектора получим систему:

,

которая эквивалентна одному уравнению . Придавая свободной переменной х₂ значение 1, получим вектор , образующий ФСР в собственном подпространстве .

Так как собственные значения , то векторы , линейно независимы и могут слу-жить базисом пространства R².

Вернемся теперь к примеру 2.

Матрица

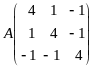
имеет собственные числа , .

Найдем собственные векторы, отвечающие значению . Система имеет вид:

.

Эта система эквивалентна одному уравнению , , , , – свободные переменные, – зависимая.

Общее решение в координатной форме имеет вид:

.

Полагая , , получим вектор ; при , получаем вектор . Векторы и образуют ФСР в собственном подпространстве .

Пусть . Система

.

Эквивалентная система имеет вид:

,

, , , – свободная переменная, , – зависимые. Общее решение в координатной форме: .

При , получим вектор , образующий ФСР собственного подпространства . Векторы , , линейно независимы и могут служить базисом пространства R³.

Рассмотрим еще один пример.

.

Характеристический многочлен :

.

Собственные числа матрицы: , . Найдем собственное подпространство V₀ для кратного корня =0 (k=2).

,

, , – свободная переменная, – базис V₀.

Заметим, что меньше кратности корня =0. Таким образом, двукратному корню =0 отвечает одномерное собственное подпространство V₀.

Пусть теперь , соответствующая система имеет вид:

,

, , – свободная переменная, , – зависимые:

и .

Хотя и линейно независимы, но они не могут образовать базис в R³.

Подведем итог сказанному. Сформулируем алгоритм поиска собственных чисел и собственных векторов матрицы.

1. Составить характеристическое уравнение:

.

2. Найти вещественные корни , характеристического многочлена (если таких нет, то нет и собственных векторов). Пусть , – соответствующие кратности этих корней. Тогда , где n – порядок квадратной матрицы А.

3. Для каждого корня составить систему линейных однородных уравнений и найти ее ФСР: , , размерность .

4. Объединить найденные фундоментальные системы по всем собственным числам . Полученная система из собственных векторов матрицы А будет линейно независимой.

Если число векторов объединенной системы , то она образует собственный базис матрицы А.