
- •Оглавление
- •Дидактический план
- •Литература
- •1. Бекелемишев, д. В. Курс аналитической геометрии и линейной алгебры [Текст] / д. В. Бекелемишев. – м. : Физматлит, 2007 (гриф умо).
- •2. Ильин, в. А. Линейная алгебра [Текст] / в. А. Ильин, э. Г. Поздняк. – м. : Физматлит, 2007 (гриф мо рф).
- •3. Кострикин, а. И. Введение в алгебру [Текст] / а. И. Кострикин. – м. : Физматлит, 2004. Кн. 2 (гриф умо).
- •Перечень компетенций
- •Тематический обзор*
- •1 Собственные числа и собственные векторы матрицы
- •1.1 Определение. Основные свойства собственных векторов
- •1.2 Характеристический многочлен
- •1.3 Собственное подпространство
- •2 Приведение симметричной матрицы к диагональному виду
- •2.1 Скалярное произведение в пространстве Rn. Процесс ортогонализации
- •2.2 Ортогональная матрица
- •2.3 Собственный базис симметричной матрицы
- •3 Квадратичная форма. Приведение к каноническому виду
- •3.1 Основные определения. Матрица квадратичной формы
- •3.2 Преобразование матрицы при линейной замене переменных
- •3.3 Приведение квадратичной формы к каноническому виду ортогональным преобразованием
- •3.4 Приведение кривой второго порядка к каноническому виду
- •3.5 Знакоопределенные квадратичные формы. Критерий Сильвестра
- •4 Линейные пространства
- •4.1 Определение линейного пространства
- •4.2 Линейная зависимость
- •4.3 Базис и координаты. Размерность пространства
- •4.4 Матрица перехода
- •4.5 Подпространство
- •4.6 Евклидовы пространства
- •5 Линейные операторы
- •5.1 Определение и примеры
- •5.2 Матрица линейного оператора
- •5.3 Самосопряженный оператор
- •Приложение 1 Перпендикуляр из точки на пространство
- •Приложение 2 о приближенном вычислении собственных значений матрицы
- •Задания для самостоятельной работы
- •1. Составьте логическую схему базы знаний по теме юниты:
- •2. Решите самостоятельно следующие задачи (номер варианта совпадает с Вашим номе-ром в списке группы):
- •Тренинг компетенций
- •1 Компетенция №1. Вычисление собственных значений и собственных векторов матрицы a порядка n
- •1.1 Пример решения типовой задачи
- •Глоссарий
- •Линейная алгебра юнита 4
Тренинг компетенций
1 Компетенция №1. Вычисление собственных значений и собственных векторов матрицы a порядка n
1.1 Пример решения типовой задачи
Условие
Найти собственные значения и собственные векторы матрицы

Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить характери-стический многочлен det(A – lE) |
|
2 |
Написать характерис-тическое уравнение |
(1 – l)((2 – l)2 – 1) = 0 или (1 – l)2(3 – l) = 0 |
3 |
Найти корни характе-ристического уравнения |
l1 = l2 = 1, l3 = 3. l1, 2 = 1 – корень кратности 2. l1, 2 = 1, l3 = 3 – собственные числа матрицы A |
4 |
Для каждого li найти собственные векторы |
l1, 2 = 1.
эта система эквивалентна одному уравнению: x1 – x2 + x3 = 0. Размерность
подпространства решений Фундаментальная система решений (ФСР) состоит из двух векторов f1, f2. Выпишем общее решение системы: {x1 = x2 – x3 x1 – зависимая переменная, x2, x3 – свободные переменные.
Решим систему методом Гаусса:
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
|
|
r(A) = 2, n = 3.
Общее решение:
ФСР:
|
5 |
Найти
ФСР для каж-дого
|
l1 = 1; , , l2 = 3; |
6 |
Объединить все най-денные ФСР |
Линейно независимая система собственных векторов матрицы А: f1, f2, f3 образуют ортогональный базис пространства R3, т.к. (f1, f2) = (f1, f3) = (f2, f3) = 0 |
1.2 Задания для самостоятельной работы
1.2.1 Задача
Найти собственные значения и собственные векторы матриц:
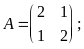 .
.
1.2.2 Задача
Найти собственные значения и собственные векторы матриц:
 .
.
1.2.3 Задача
Найти собственные значения и собственные векторы матриц:
 .
.
1.2.4 Задача
Найти собственные значения и собственные векторы матриц:
 .
.
1.2.5 Задача
Найти собственные значения и собственные векторы матриц:
 .
.
1.2.6 Задача
Найти собственные значения и собственные векторы матриц:
 .
.
2 Компетенция №2. Построение ортогональной системы векторов по заданной линейно независимой системе
2.1 Пример решения типовой задачи
Условие
Ортогонализовать
систему векторов пространства R4:
f1=(1,–1,2,0),
f2=(0,0,1,1),
![]() .
.
Решение
Убедимся, что данные векторы линейно независимы и не являются взаимно ортогональными. Для этого найдем ранг системы векторов:

Ранг системы {f} равен трем, все векторы линейно независимы.
Проверим
ортогональность (f1,
f2)
= 2
![]() 0,
(f1,
f3)
= 3
0,
(f2,
f3)
= 2
0.
0,
(f1,
f3)
= 3
0,
(f2,
f3)
= 2
0.
Векторы не являются взаимно ортогональными.
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Положить g1 = f1 |
g1 = (1, – 1, 2, 0) |
2 |
g2 = f2 – l g1, где
|
(g1, f1) = 2, (g1, g1) = 6.
|
3 |
|
(g1,
f3)
= 3; (g1,
g1)
= 6; (g2,
f3)
= 1; (g2,
g2)
=
|
4 |
Выписать полученную ортогональную систему g1, g2, g3 |
g1 = (1, – 1, 2, 0), g2
=
g3
= |
2.2 Задания для самостоятельной работы
2.2.1 Задача
Ортогонализовать данную систему векторов:
f1 = (– 2, 2)
f2 = (3, 4)
2.2.2 Задача
Ортогонализировать данную систему векторов:
f1 = (1, 0, 1)
f2 = (–1, – 1, –1)
f3 = (1, 2, –1)
2.2.3 Задача
Ортогонализовать данную систему векторов:
f1 = (1, 1, 1, 0)
f2 = (1, –1, 0, 1)
f3 = (2, 0, –2, 1)
3 Компетенция №3 Составление матрицы данной квадратичной формы и проверка ее положительной определенности
3.1 Пример решения типовой задачи
Условие 1
Выписать матрицу А квадратичной формы
![]()
Проверить знакоопределенность квадратичной формы, используя критерий Сильвестра.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать симметричную матрицу квадратичной формы |
Для
данной квадратичной формы a11
= – 2; 2a12
= 8; 2a13
= – 2;
|
2 |
Вычислить все угловые миноры мат-рицы А |
D1 = – 2 <0.
|
3 |
Определить знак квадратичной фор-мы. Будет ли форма положительно определенной? |
По критерию Сильвестра Q(x) не является поло-жительно определенной, т.к. не все угловые миноры положительны. Знаки угловых миноров чередуются, причем, D1 < 0, значит Q(x) отрицательно определена |
Условие 2
Найти все значения параметра , при которых квадратичная форма
![]()
будет положительно определена.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать матрицу квадратичной фор-мы |
|
2 |
Вычислить все угловые миноры мат-рицы А |
D1 = 1 > 0.
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
3 |
Применить критерий Сильвестра положительной определенности |
D1 = 1 > 0. D2 = 1 > 0. D3 = –a2 + 4a – 3 = –(a – 1)( a – 3) > 0 для всех aÎ(1, 3). Ответ: если параметр aÎ(1, 3), то квадратичная форма Q(x) положительно определена |
3.2 Задания для самостоятельной работы
3.2.1 Задача
Определить знак квадратичной формы:
![]()
3.2.2 Задача*
Определить знак квадратичной формы:
![]()
3.2.3 Задача
Определить знак квадратичной формы:
![]()
3.2.4 Задача*
Определить знак квадратичной формы:
![]()
3.2.5 Задача
Найти наименьшее целое значение параметра , при котором квадратичная форма поло-жительно определена:
![]()
Замечание. Для решения задач, отмеченных (*), следует применить критерий неотрицатель-ной определенности.
4 Компетенция №4. Приведение квадратичной формы к каноническому виду ортогональным преобразованием
4.1 Пример решения типовой задачи
Условие
Привести квадратичную форму
![]()
к каноническому виду ортогональным преобразованием.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать симметричную мат-рицу А квадратичной формы |
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
2 |
Найти собственные числа l1, l2, l3 матрицы А |
Характеристический многочлен
Характеристическое уравнение: det(A – lE) = 0, или P(l) = (5 – l)(l2 – 16) = 0. l1 = – 4, l2 = 4, l3 = 5. Все корни различные и просты (кратности 1) |
3 |
Найти собственные векторы f1, f2, f3, отвечающие собственным значениям l1, l2, l3 |
а) l1 = – 4 Соответствующая система уравнений:
Решим систему методом Гаусса:
x3 – свободная переменная. Собственный
вектор (базисный пространства
f1 = (– 1, 0, 1) б) l2 = 4 Соответствующая система уравнений:
Решим систему методом Гаусса:
x3 – свободная переменная. Собственный вектор (базисный пространства ) f2 = (1, 0, 1). в) l3 = 5 Соответствующая система уравнений:
Решим систему методом Гаусса:
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
|
|
x2 – свободная переменная. Собственный
вектор (базисный пространства
|
4 |
Ортогонализовать базис f1, f2, f3 |
Полученный собственный базис
(g1 = f1; g2 = f2; g3 = f3) уже ортогональный т.к. (f1, f2) = (f1, f3) = (f2, f3) = 0. l1¹l2¹l3 – различным собственным значениям отвечают ортогональные собственные векторы симметричной мат-рицы |
5 |
Нормировать базис {g} |
u1, u2, u3 – ортонормированный собственный базис мат-рицы А |
6 |
Составить ортогональную мат-рицу перехода С от базиса {e} к базису {u} |
|
7 |
Сделать замену переменных x=Cy. Выписать канонический вид квадратичной формы |
В
координатах y1,
y2,
y3
квадратичная форма
|
8 |
Записать обратное преобразо-вание координат |
В
силу ортогональности матрицы С
обратная матрица
В старых координатах x1, x2, x3 Q(x) = – 2(x1 – x3)2 + 2(x1 + + x3)2 + 5 x22 |
4.2 Задания для самостоятельной работы
4.2.1 Задача
Привести квадратичные формы к каноническому виду (к сумме квадратов).
![]() .
.
4.2.2 Задача
Привести квадратичные формы к каноническому виду (к сумме квадратов).
![]() .
.
4.2.3 Задача
Привести квадратичные формы к каноническому виду (к сумме квадратов).
![]() .
.
4.2.4 Задача
Привести квадратичные формы к каноническому виду (к сумме квадратов).
![]() .
.
Указание: характеристический многочлен равен:
P( ) = – ( – 7)2( + 2)2.
5 Компетенция № 5. Приведение к каноническому виду центральной кривой второго порядка
5.1 Пример решения типовой задачи
Условие
Привести кривую второго порядка 3x2 + 2xy + 3y2 – 4 = 0 к каноническому виду.
Решение
Общее уравнение кривой второго порядка имеет вид:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0,
где хотя бы один из коэффициентов A, B, C отличен от нуля (A2 + B2 + C2 > 0).
Здесь A = 3, B = 1, C = 3, D = E = 0; F=-4; AC – B2 = 9 – 1 > 0.
Следовательно, кривая центральная, эллиптического типа.
Координаты центра x0, y0 находим из системы:
 или
или
 .
.
Центр находится в начале координат, перенос осей не нужен, требуется лишь поворот систе-мы координат.
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать матрицу квад-ратичной формы |
Q(x, y) = 3x2 + 2xy + 3y2
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
2 |
Найти собственные числа l1, l2 |
l1 = 4, l2 = 2 |
3 |
Найти ортонормирован-ные собственные векто-ры u1, u2 |
l1 = 4;
l2 = 2;
|
4 |
Составить матрицу С пе-рехода от базиса {e} к базису {u} |
Стандартный базис: e1 = (1, 0); e2 = (0, 1). Новый собственный базис: u1, u2. Матрица перехода от {e} к {u}:
|
5 |
Записать канонический вид кривой l1(x¢)2 +l2(y¢)2+F= 0 |
Перейдем к новым координатам x¢, y¢:
В новой системе координат x¢, y¢ уравнение кривой имеет вид: 4(x¢)2 + 2(y¢)2 – 4 = 0 |
6 |
Определить тип кривой и сделать чертеж |
Приведем полученное уравнение к каноническому виду:
Новые
оси OX¢,
OY¢
направлены по собственным векторам
u1,
u2,
переход к новым осям осуществлен
поворотом на угол
|
5.2 Задания для самостоятельной работы
5.2.1 Задача
Привести следующие кривые второго порядка к каноническому виду:
2xy – 4x2 – y2 – 15 = 0.
5.2.2 Задача
Привести следующие кривые второго порядка к каноническому виду:
x2 – 6xy + y2 – 16 = 0.
5.2.3 Задача
Привести следующие кривые второго порядка к каноническому виду:
5x2 – 2xy + 5y2 = 0.
6 Компетенция №6. Проверка условий линейного подпространства для множества W
6.1 Пример решения типовой задачи
Условие 1
Проверить, образует ли линейное подпространство множество
W1 = {x = (x1, x2, x3, x4) R4 | 2x1 + x4) = 0}.
Множество
W1
состоит из тех
векторов пространства R4,
для координат которых выполняется
условие 2x1
+ x4
= 0 (например,
![]() = (– 2, 3, 0, 4)
W1,
а вектор
= (– 2, 3, 0, 4)
W1,
а вектор
![]() = (3, 1, 1, 0)
W1).
= (3, 1, 1, 0)
W1).
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить вектор z = ax + by, где a, b – пропорциональные числа, x, y Î W1 |
Пусть x = (x1, x2, x3, x4) и y = (y1, y2, y3, y4) Î W1, т.е. обладают свойством
Составим вектор z = ax + by = (ax1 + by1; ax2 + by2; ax3 + by3; ax4 + by4) = = (z1, z2, z3, z4) |
2 |
Выяснить, принадлежит ли век-тор z множеству W1 |
Найдем для вектора z сумму координат 2z1 + z4. 2z1 + z4 = 2(ax1 + by1) + (ax4 + by4) = a(2x1 + x4) + b(2y1 + + y4) = 0 (см. (*)). Для вектора z выполнены условия, определяющие мно-жество W1 т.е. z Î W1 |
3 |
Сделать вывод |
Линейные операции над векторами множества W1 не выво-дят из множества W1. Следовательно, W1 – подпростран-ство |
Условие 2
Проверить, образует ли линейное подпространство множество
W2 = {x = (x1, x2, x3, x4) R4 | 2x1 + x4) = 0}.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить вектор z = ax + by, где a, b – произво-льные числа, x, y Î W2. |
Пусть x = (x1, x2, x3, x4) Î W2 и y = (y1, y2, y3, y4) Î W2, т.е.
Составим вектор z = ax + by = (z1, z2, z3, z4), где zi = axi + byi(i = 1, 2, 3, 4) |
2 |
Выяснить, принад-лежит ли вектор z множеству W2. |
2z1 + z4 = 2(ax1 + by1) + (ax4 + by4) = a(2x1 + x4) + b(2y1 + y4) = a + b ¹ 1, для произвольных a, b т.е. z Ï W2 |
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
3 |
Сделать вывод |
Линейные операции над векторами множества W2 выводят за множества W2. Следовательно, W2 не является подпространством. Таким образом, совокупность решений неоднородного уравнения 2x1 + x4 = 1 не образует подпространства в отличие от подпро-странства решений однородного уравнения 2x1 + x4 = 0. Совокуп-ность решений неоднородной системы – сдвиг подпространства решений однородной системы (см. юниту 1) |
Условие 3
Проверить,
образует ли подпространство множество
W
всех
четных функций пространства
![]() .
.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить вектор j(x) = af(x) + bg(x), где a, b – произвольные числа, f(x), g(x) ÎW |
Пусть f(x), g(x) – четные, непрерывные на (–1, 1) функции, т.е. f, g Î W. Тогда
Составим функцию j(x) = af(x) + bg(x) |
2 |
Выяснить, принадлежит ли вектор j(x) множеству W |
Сравним j(x) и j(– x): j(– x) = af(– x) + bg(– x) = af(x) + bg(x) = j(x), т.к. выполняются равенства (*). Итак, j(– x) = j(x), функция j(x) – четная, j(x) Î W |
3 |
Сделать вывод |
Линейные операции над четными функциями оставляют функ-цию четной, т.е. множество четных функций является под-пространством. Аналогично можно убедиться, что множество нечетных функ-ций пространства С(–1, 1) является подпространством |
6.2 Задания для самостоятельной работы
6.2.1 Задача
Будет ли подпространством подмножество V R4, определенное следующим образом:
V = {x = (x1, x2, x3, x4) R4 | x3 = 2x2}.
6.2.2 Задача
Будет ли подпространством подмножество V R4, определенное следующим образом:
V = {x = (x1, x2, x3, x4) R4 | x3 > 2x2}.
6.2.3 Задача
Будет ли подпространством подмножество V R4, определенное следующим образом:
V = {x = (x1, x2, x3, x4) R4 | x1 – целое число}.
6.2.4 Задача
Будет ли подпространством подмножество V R4, определенное следующим образом:
V = {x = (x1, x2, x3, x4) R4 | x1 + x2 + x3 + x4 = 0}.
6.2.5 Задача
Образует ли подпространство множество W всех линейных функций
f(x) = ax + b,
где a, b – произвольные числа.
6.2.6 Задача
Образует ли подпространство множество W всех многочленов третьей степени от переменной x.
7 Компетенция №7. Проверка условий образования базиса линейного подпространства из данной системы векторов
7.1 Пример решения типовой задачи
Условие 1
Выяснить, образует ли система векторов f1(2,–1,1), f2(0,1,–1), f3(2,1,–1) базис в пространстве R3.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать стандартный базис данного линейного пространства и определить размерность пространства |
Стандартный базис R3: e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1). dim R3 = 3 |
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
2 |
Определить координаты данной систе-мы в стандартном базисе |
В стандартном базисе координаты векторов совпа-дают с их компонентами: f1 = 2e1 – e2 + e3 = (2, – 1, 1)e f2 = e2 – e3 = (0, 1, – 1)e f3 = 2e1 + e2 – e3 = (2, 1, – 1)e |
3 |
Составить матрицу А из координат векторов {f} в базисе {e} |
|
4 |
Найти ранг матрицы А |
Определим rank A методом Гаусса.
rank А=2 |
5 |
Сделать вывод |
rank A ¹ dim R3, система f1, f2, f3 не образует базис |
Условие 2
Образует ли система многочленов 1 =1, 2 = x, 3 = x2 + 2x + 1, 4 = x3 – x2 базис в прост-ранстве многочленов степени n 3.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать стандартный базис пространства и определить размерность пространства |
В пространстве P многочленов степени £ 3 стандартный базис состоит из функций: e1 = 1, e2 = x, e3 = x2, e4 = x3 dim P = 4 |
2 |
Определить координаты системы векторов {j} в стандартном базисе {e} |
j1 = e1 = (1, 0, 0, 0)e j2 = x = e2 = (0, 1, 0, 0)e j3 = 1 + 2x + x2 = e1 + 2e2 + e3 = (1, 2, 1, 0)e j4 = – x2 + x3 = – e3 + e4 = (0, 0, – 1, 1)e |
3 |
Составить матрицу А из коор-динат векторов {j} в базисе {e} |
|
4 |
Найти r (А) |
Определим rank A методом Гаусса.
rank A=4 |
5 |
Сделать вывод |
r (A) = 4 = dim P, система j1, j2, j3, j4 образует базис |
7.2 Задания для самостоятельной работы
7.2.1 Задача
Выяснить, образует ли данная система векторов базис линейного пространства.
f1 = (– 1, 2), f2 = (2, – 4) R2.
7.2.2 Задача
Выяснить, образует ли данная система векторов базис линейного пространства.
f1 = (1, 4, 6), f2 = (1, – 1, 1), f3 = (1, 1, 3) R3.
7.2.3 Задача
Выяснить, образует ли данная система векторов базис линейного пространства.
f1 = (1, – 1, 2), f2 = (– 1, 1, – 1), f3 = (2, – 1, 1) R3.
7.2.4 Задача
Выяснить, образует ли данная система векторов базис линейного пространства.
1(x) = 1+x+х2; 2(x) = 1 + 2x + x2; 3(x) = 1 + 3x + x2
в пространстве P многочленов степени 2.
7.2.5 Задача
Выяснить, образует ли данная система векторов базис линейного пространства.
1(x) = x; 2(x) = x2; 3(x) = (1 + x)2
в пространстве P многочленов степени 2.
7.2.6 Задача
Выяснить, образует ли данная система векторов базис линейного пространства.
1(x) = shx; 2(x) = chx
в линейной оболочке функций e1(x) = ex, e2(x) = e–x.
8 Компетенция №8. Отыскание координат вектора в новом базисе, если он задан в базисе {e}
8.1 Пример решения типовой задачи
Условие 1
Найти координаты вектора x = (1,1,1) в базисе f1(1,2,0), f2(1,3,0), f3(1,0,1), если все векторы заданы в базисе {e}.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Определить координаты новой системы {f} по ста-рому базису {e} |
Стандартный базис пространства R3: e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1). Координаты системы {f} по старому базису {e} совпадают с компонентами векторов {f}. f1 = e1 + 2e2 f2 = e1 + 3e2 f3 = e1 + e3 |
2 |
Записать матрицу перехода С от старого базиса {e} к новому базису {f} |
Столбцами матрицы С служат координаты векторов нового базиса {f} по старому {e} |
3 |
Выписать зависимость «старых» координат векто-ра x от «новых» координат в базисе {f}. xe = Cxf |
Пусть координаты вектора x в базисе {f} будут xf = (y1, y2, y3), тогда
|
4 |
Найти обратную матрицу C–1 |
Найдем матрицу C–1 с помощью алгебраических дополнений.
A11 = 3; A21 = – 1; A31 = – 3; A12 = – 2; A22 = 1; A32 = 2; A13 = 0; A23 = 0; A33 = 1.
|
5 |
Вычислить координаты вектора x в новом базисе {f}: xf = C–1xe |
Замечание. Поставленную задачу решим не вычисляя C–1. Для этого разложим вектор x по новому базису: {f}: x = y1f1 + y2f2 + + y3f3. Выразим левую и правую части равенства через векторы e1, e2,…,e3: e1 + e2 + e3 = y1(e1 + 2e2) + y2(e1 + 3e2) + y3(e1 + e3), (1 – y1 – y2 – y3)e1 + (1 – 2y1 – 3y2)e2 + (1 – y3)e3 = 0. Так как, e1, e2, e3 линейно независимы, то полученная линейная комбинация тривиальная:
|
Условие 2
Найти координаты вектора P(x) = x2 + x в базисе из полиномов Лежандра f1 = 1, f2 = x,
f3
=
![]() ,
f4
=
,
f4
=
![]() .
.
(Пространство многочленов степени 3.)
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Определить координаты нового базиса {f} по старому базису {e} |
Стандартный базис пространства: e1 = 1, e2 = x, e3 = x2, e4 = x3. f1 = 1 = e1 = (1, 0, 0, 0) f2 = x = e2 = (0, 1, 0, 0)
f3
=
f4
=
|
2 |
Записать матрицу перехода С от старого базиса {e} к новому базису {f} |
|
3 |
Выписать зависимость «старых» коор-динат вектора P(x) от «новых» координат в базисе {f} |
Пусть координаты многочлена P(x) по полино-мам Лежандра будут y1, y2, y3, y4; в стандарт-ном базисе многочлен P(x) имеет координаты: P(x) = x + x2 = e2 + e3 = (0, 1, 1, 0), тогда
|
4 |
Найти обратную матрицу C–1 |
C–1 будем искать методом Гаусса
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
|
|
Итак,
|
5 |
Вычислить координаты вектора P(x) в но-вом базисе {f} Pf = C–1Pe |
x + x2 = f1 + 1f2 + 1f3 = × 1 + 1x + 1×(x2 ) |
8.2 Задания для самостоятельной работы
8.2.1 Задача
Найти координаты вектора x в базисе {f}, если все векторы заданы в стандартном базисе {e}.
f1 = (1,1,2), f2 = (2,–1,0), f3 = (–1,1,1), x = (6,–1,3).
8.2.2 Задача
Найти координаты вектора x в базисе {f}, если все векторы заданы в стандартном базисе {e}.
f1 = (2,5,–1), f2 = (–1,–3,0), f3 = (2,3,–2), x = (1,2,0).
8.2.3 Задача
Найти координаты вектора x в базисе {f}, если все векторы заданы в стандартном базисе {e}.
f1 = (1,0,1), f2 = (1,1,0), f3 = (0,1,–3), x = (4,–2,1).
8.2.4 Задача
Найти координаты многочлена P(x) = 3x2 – 2x + 6 в базисе f1 = x, f2 = x + 1, f3 = (1 + x)2; рассматривается пространство многочленов степени 2, исходный базис – стандартный.
8.2.5 Задача
В линейной оболочке L(ex, e–x) задана функция (x) = ex + 2e–x. Найти координаты (x) в новом базисе f1 = chx, f2 = shx.
9 Компетенция №9. Проверка линейности заданного оператора
9.1 Пример решения типовой задачи
Условие 1
Проверить линейность оператора A : R3 R3 , где
Aх = (x1 + x3, x2, 2x1 + x3 ) для x = (x1, x2, x3) R3.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить вектор z = ax + by, где a, b – любые числа, x, y Î R3 |
z = (z1, z2, z3) = a(x1¸ x2, x3) + b(y1, y2, y3) = (ax1 + by1, ax2 + by2, ax3 + by3) |
2 |
Найти образ Az = A(ax + by) |
Az = (z1 + z3, z2, 2z1 + z3), где z1 + z3 = ax1 + by1 + ax3 + by3 = a(x1 + + x3) + b(y1 + y3) z2 = ax2 + by2 2z1 + z3 = 2(ax1 + by1) + ax3 + by3 = a(2x1 + x3) + b(2y1 + y3) |
3 |
Найти образы Ax и Ay |
Ax = (x1 + x3, x2, 2x1 + x3) Ay = (y1 + y3, y2, 2y1 + y3) |
4 |
Проверить, совпадают ли векторы Az и aAx + bAy |
aAx + bAy = a(x1 + x3, x2, 2x1 + x3) + b(y1 + y3, y2, 2y1 + y3) = (a(x1 + + x3)+ b(y1 + y3); ax2 + by2; a(2x1 + x3) + b(2y1 + y3)) Сравнивая координаты вектора aAx + bAy с соответствующими координатами вектора Az убеждаемся, что aAx + bAy = Az |
5 |
Сделать вывод |
Так как aAx + bAy = A(ax + by), то (оператор) преобразование А – линейно |
Условие 2
Проверить линейность преобразования Ax = x + a, где x, a V, причем a – фиксированный вектор.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить вектор z = ax + by |
z = ax + by, где x, y Î V, a, b –любые числа |
2 |
Найти образ Az = A(ax + by) |
Az = A(ax + by) = z + a = ax + by + a |
3 |
Найти образы Ax и Ay |
Ax = x + a, Ay = y + a |
4 |
Проверить, совпадают ли векторы Az и aAx + bAy |
aAx = ax + aa bAy = by + ba. aAx + bAy = ax + by + (a + b)a. Сравнивая образы A(ax + by) (п. 2) и aAx + bAy, получим, что они совпадают лишь в случае a + b = 1 (не для всяких a, b) |
5 |
Сделать вывод |
Так как A(ax + by) ¹ aAx + bAy для любых a, b, то преобразование А не является линейным |
Условие 3
В
пространстве
![]() дважды дифференцируемых на (a,b)
функции f(t)
задан оператор диф-ференцирования
дважды дифференцируемых на (a,b)
функции f(t)
задан оператор диф-ференцирования
D : f(t) t f(t) + f(t).
Проверить линейность оператора D.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить функ-цию j(t) = af(t) + bg(t) |
j(t) = af(t) + bg(t), здесь a, b –любые числа, f(t), g(t) Î С2(a,b) |
2 |
Найти образ D(j(t)) |
D(j(t)) = t × j¢¢(t) + j¢(t) = t(af(t) + bg(t))¢¢ + (af(t) + bg(t))¢ = a(tf¢¢(t) + +f¢(t)) + b(g¢¢(t)t + g¢(t)). (Использовали линейность операции дифференцирования: по правилам дифференцирования производная от суммы функций равна сумме производных, числовой множитель можно вынести за знак производной) |
3 |
Найти образы D(f(t)) и D(g(t)) |
D(f(t)) = tf¢¢(t) + f¢(t) D(g(t)) = tg¢¢(t) + g¢(t) |
4 |
Проверить, совпа-дают ли D(af + bg) и aD(f) + bD(g) |
aD(f) + bD(g) = a(tf¢¢+ f¢) + b(tg¢¢+ g¢) = t(af¢¢+ bg¢¢) + af¢+bg¢. Сравнивая результаты п. 2 с последним равенством, получаем, что D(af + bg) = aD(f) + bD(g) |
5 |
Сделать вывод |
Оператор D : f(t) ® t × f¢¢(t) + f¢(t) – линейный |
9.2 Задания для самостоятельной работы
9.2.1 Задача
Проверить линейность заданного преобразования
A : R3 R3; Ax = (x3, x1, x2), где x = (x1, x2, x3) R3.
9.2.2 Задача
Проверить линейность заданного преобразования
A : R3 R3; Ax = (x1 + 1, x2, 2x3), где x = (x1, x2, x3) R3.
9.2.3 Задача
Проверить линейность заданного преобразования
A : V V; Ax = (a, a)x,
где a, x – векторы евклидова пространства V, a – фиксированный вектор.
9.2.4 Задача
Проверить линейность заданного преобразования
A : V V; Aх = a,
где a, x V, a – фиксированный вектор.
9.2.5 Задача
Проверить линейность заданного преобразования
D : f(t) f(t) + f(t),
где f(t) – дифференцируемая на (a, b) функция.
9.2.6 Задача
Проверить линейность заданного преобразования
D : f(t) f(t) + С,
где f (t) – дважды дифференцируемая на (a, b) функция, С = const.
10 Компетенция №10. Составление матрицы оператора A в заданном базисе {e}
10 Пример решения типовой задачи
Условие 1
Написать матрицу оператора A : R3 R3, где Ax = (x1 + x3, x2, 2x1 + x3 ) для x = (x1, x2, x3) R3 в стандартном базисе.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Найти образцы базисных векторов
|
Применим преобразование А к базисным векторам e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1).
|
2 |
Записать в k-ый столбец матрицы A(k = 1, 2, 3) координаты
вектора
|
|
Условие 2
В пространстве многочленов степени 3 задан оператор
D
: p(t)
t
p(t)
+ p(t)
=

Написать матрицу этого оператора в стандартном базисе 1, t, t2, t3.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Найти образцы базисных векторов D(ei) (i = 1, 2, 3, 4) |
D(e1) = D(1) = 0 = (0, 0, 0, 0) D(e2) = D(t) = 0 + 1 = (1, 0, 0, 0) D(e3) = D(t2) = 2×t + 2t = 4t = (0, 4, 0, 0) D(e4) = D(t3) = 3×2×t×t + 3t2 = 9t2 = (0, 0, 9, 0) |
2 |
Запишем координаты базисных векторов в столбцы матрицы А |
|
10.2 Задания для самостоятельной работы
10.2.1 Задача
Написать матрицу преобразования А в заданном базисе
A : R3 R3; Ax = (x3,x1,x2 ), где x = (x1,x2,x3) R3; базис стандартный.
10.2.2 Задача
Написать матрицу преобразования А в заданном базисе
A : R3 R3; Ax = (a,a)x, где x = (x1,x2,x3) R3; a R3 – фиксированный; базис стандартный.
10.2.3 Задача
Написать матрицу преобразования А в заданном базисе
D : p(t) p(t) + p(t), где p(t) – многочлен степени 3; базис стандартный 1, t, t2, t3.
10.2.4 Задача
Написать матрицу оператора D в стандартном базисе et, e–t
D : f(t) f(t) + f(t), где f(t) = aet+ be–t(f(t) L(et, e–t)), a, b – любые числа.
10.2.5 Задача
Написать матрицу оператора D, заданного в задаче № 4 в базисе shx, chx.
11 Компетенция №11. Отыскание координат образа y=Ax в заданном базисе {e}
11.1 Пример решения типовой задачи
Условие 1
Найти координаты образа y = Ax, где Ax = (x1 + x3, x2, 2x1 + x3), x = (x1, x2, x3) = (3,–1,2) R3 в стандартном базисе.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Написать матрицу опе-ратора А в базисе {e} |
(см. задание 1, тр. 10) |
2 |
Выписать вектор–стол-бец xe и определить ко-ординаты образа y = Ax в базисе {e}: ye = Axe |
Замечание. Координаты образа у можно получить непосредст-венно применяя преобразование А к данному вектору x = (3,–1,2): y = Ax = (3+ 2, – 1,2×3 + 2) = (5,–1,8) |
Условие 2
Найти координаты образа D(p), где p = 2 – 3t2 + 2 t3,
D : p(t) t p(t) + p(t);
пространство многочленов степени 3, базис стандартный.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Написать матрицу А оператора D в заданном базисе |
(см. задание 2, тр. 10) |
2
|
Выписать
вектор–столбец коорди-нат многочлена
p(t)
в заданном базисе и найти координаты
образа D(p)
в том же базисе
|
Замечание. Применим оператор D к многочлену p(t):
D(p) = (0, – 12, 18, 0) – координаты образа в стан-дартном базисе. Так, для вычисления координат образа можно испо-льзовать любой способ, в зависимости от ситуации |
11.2 Задания для самостоятельной работы
11.2.1 Задача
Найти координаты вектора–образа в заданном базисе:
A : R3 R3; Ax = (x3, x1, x2 ), где x = (x1, x2, x3) R3;
найти Ax для x = (1,–2,0), базис стандартный.
11.2.2 Задача
Найти координаты вектора–образа в заданном базисе:
A : R3 R3; Ax = x,
где – фиксировано, x R3; найти Ax для x = (3,1,–1), базис стандартный.
11.2.3 Задача
Найти координаты вектора–образа в заданном базисе:
A : R3 R3; Ax = (x, a)a,
где x R3; a = (1,2,1) – фиксированный вектор, найти Ax для x = (3,–4,2), базис стандартный, скалярное произведение обычное.
11.2.4 Задача
Найти координаты вектора–образа в заданном базисе:
D : f(t) t p(t) + p(t),
p(t) – многочлен степени 3, найти D(p), если p = 2 t3 – 3t2 + 1; базис стандартный.
11.2.5 Задача
В линейной оболочке L(e3t, e–3t), задан оператор D : f f. Найти D(f), для f = 2e–3t в базисе sh3t, ch3t.
12 Компетенция № 12. Определение изменения матрицы оператора A при переходе к новому базису
12.1 Пример решения типовой задачи
Условие 1
Определить матрицу оператора A в базисе {f}, если f1 = e1 – e2 + e3, f2 = – e1 + e2 – 2e3, f3 = 2e2 – e3; в базисе {e} матрица оператора равна
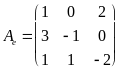 .
.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить матрицу перехода С от {e} к {f}. Вычислить С–1 |
|
2 |
Записать матрицу Ае оператора А в базисе {e} |
Матрица
Ае
задана
|
3 |
Вычислить матрицу оператора в базисе {f}:
|
|
Условие 2
В пространстве многочленов степени 2 задан оператор
D : p(t) 2p – p.
Найти матрицу оператора D в стандартном базисе e1 = 1, e2 = t, e3 = t2 и в базисе f1 = t2 + 1, f2 = t – 1, f3 = t.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить матрицу перехода от {e} к {f}. Вычислить С–1 |
f1 = t2 + 1 = e1 + e3 = (1, 0, 1), f2 = t – 1 = – e1 + e2 = (– 1, 1, 0), f3 = t = e2 = (0, 1, 0).
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
2 |
Записать матрицу Ае оператора D в базисе {e} |
D(e1) = 2×1 – 0 = 2 e1 = (2, 0, 0), D(e2) = 2× t–1 = – e1 + 2e2 = (– 1, 2, 0), D(e3) = 2t2 – 2t = –2e2 + 2e3 = (0, – 2, 2),
|
3 |
Вычислить матрицу Аf оператора D в базисе {f}: Аf = С–1 АеС |
|
12.2 Задания для самостоятельной работы
12.2.1 Задача
Линейный оператор А в базисе {e} имеет матрицу
 .
.
Найти матрицу этого оператора в базисе {f}, если f1 = 2e1 + 3e2 + e3; f2 = 3e1 + 4e2 + e3; f3 = e1 + 2e2 + 2e3.
12.2.2 Задача
В пространстве R3 оператор A : R3 R3, Ax = (2x1, x2, x3 + x1), где x = (x1, x2, x3) R3. Написать матрицу оператора Ae в стандартном базисе {e} и Af в базисе {f}, где f1 = e1 + e2 + e3; f2 = 4e2 + e3; f3 = e2 + 2e3.
12.2.3 Задача
В линейной оболочке L(et, e–t) задан оператор
D(f)
: f(t)
2f –
![]() .
.
Написать матрицу оператора D в базисах et, e–t и cht, sht.
13 Компетенция №13 Определение матрицы линейного оператора A в стандартном базисе {e} и в базисе {f}
13.1 Пример решения типовой задачи3
Условие
В
пространстве Р
многочленов степени
2 задана система векторов f1
= t
(t
+ 1), f2
= t,
f3
= 1 и преобразование А
: p(t)
t
![]() .
Убедиться, что {f}
– базис, оператор А
– линейный. Написать матрицы оператора
А
в базисах {e}
и {f},
где {e}
– стандартный базис 1, t,
t2.
.
Убедиться, что {f}
– базис, оператор А
– линейный. Написать матрицы оператора
А
в базисах {e}
и {f},
где {e}
– стандартный базис 1, t,
t2.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать стандартный базис |
e1 = 1, e2 = t, e3 = t2, dim p = 3 |
2 |
Выяснить, образует ли сис-тема {f} базис |
Координаты векторов {f} в базисе {e}:
Найдем ранг системы векторов {f}
Ранг системы {f} равен dim p, f1, f2, f3 – базис пространства Р |
3 |
Проверить линейность опе-ратора А |
Пусть f, g Î P – любые многочлены степени £ 2, a, b – произвольные числа, тогда A(af + bg) = t(af + bg)¢ = atf¢ + btg¢ = aA(f) + bA(g); A – линейный оператор |
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
4 |
Выписать матрицу перехода С от {e} к {f}. Вычислить С–1 |
Координаты векторов f1, f2, f3 по базису {e} (см. п. 2) запишем в столбцы матрицы С:
|
5 |
Написать матрицы опера-тора А в базисах {e} и {f} |
Применим преобразование А к базисным векторам {e}: Ae1 = 0 = 0×e1 + 0×e2 + 0×e3 = (0, 0, 0), Ae2 = t = 0×e1 + 1×e2 + 0×e3 = (0, 1, 0), Ae3 = 2t2 = 0×e1 + 0×e2 + 2×e3 = (0, 0, 2),
Af1 = 2t2 + t = 2(t2 + t) – t = 2f1 – f2 = (2, – 1, 0), Af2 = t = f2 = (0, 1, 0), Af3 = 0 = (0, 0, 0),
|
6 |
Убедиться, что
|
|
13.2 Задания для самостоятельной работы
13.2.1 Задача
В пространстве многочленов степени 2 задана система векторов {f} и преобразование А. Убедиться, что {f} – базис, оператор А – линейный. Написать матрицы оператора А в базисе {f} и в стандартном базисе {e}.
f1 = t; f2 = 1 + t2; f3 = 1 – t2; A(p) = p + p.
13.2.2 Задача
В пространстве многочленов степени 2 задана система векторов {f} и преобразование А. Убедиться, что {f} – базис, оператор А – линейный. Написать матрицы оператора А в базисе {f} и в стандартном базисе {e}.
f1 = (1 +t2); f2 = 1 + t; f3 = 1; A(p) = 2p – p.
13.2.3 Задача
В пространстве многочленов степени 2 задана система векторов {f} и преобразование А. Убедиться, что {f} – базис, оператор А – линейный. Написать матрицы оператора А в базисе {f} и в стандартном базисе {e}.
f1 = (t2 – 1); f2 = t; f3 = t + 1; A(p) = t p.



 ,
,
 .
. .
.
 ,
,


















 ;
;
 ;
;
 .
.





 матрица
поворота на угол a
матрица
поворота на угол a
 – эллипс
с полуосями a
= 1,
– эллипс
с полуосями a
= 1,




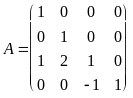
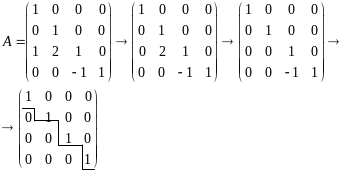












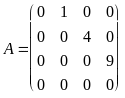 – матрица
заданного оператора D
в стандартном базисе
– матрица
заданного оператора D
в стандартном базисе













 .
.
 ,
,