
- •Оглавление
- •Дидактический план
- •Литература
- •1. Бекелемишев, д. В. Курс аналитической геометрии и линейной алгебры [Текст] / д. В. Бекелемишев. – м. : Физматлит, 2007 (гриф умо).
- •2. Ильин, в. А. Линейная алгебра [Текст] / в. А. Ильин, э. Г. Поздняк. – м. : Физматлит, 2007 (гриф мо рф).
- •3. Кострикин, а. И. Введение в алгебру [Текст] / а. И. Кострикин. – м. : Физматлит, 2004. Кн. 2 (гриф умо).
- •Перечень компетенций
- •Тематический обзор*
- •1 Собственные числа и собственные векторы матрицы
- •1.1 Определение. Основные свойства собственных векторов
- •1.2 Характеристический многочлен
- •1.3 Собственное подпространство
- •2 Приведение симметричной матрицы к диагональному виду
- •2.1 Скалярное произведение в пространстве Rn. Процесс ортогонализации
- •2.2 Ортогональная матрица
- •2.3 Собственный базис симметричной матрицы
- •3 Квадратичная форма. Приведение к каноническому виду
- •3.1 Основные определения. Матрица квадратичной формы
- •3.2 Преобразование матрицы при линейной замене переменных
- •3.3 Приведение квадратичной формы к каноническому виду ортогональным преобразованием
- •3.4 Приведение кривой второго порядка к каноническому виду
- •3.5 Знакоопределенные квадратичные формы. Критерий Сильвестра
- •4 Линейные пространства
- •4.1 Определение линейного пространства
- •4.2 Линейная зависимость
- •4.3 Базис и координаты. Размерность пространства
- •4.4 Матрица перехода
- •4.5 Подпространство
- •4.6 Евклидовы пространства
- •5 Линейные операторы
- •5.1 Определение и примеры
- •5.2 Матрица линейного оператора
- •5.3 Самосопряженный оператор
- •Приложение 1 Перпендикуляр из точки на пространство
- •Приложение 2 о приближенном вычислении собственных значений матрицы
- •Задания для самостоятельной работы
- •1. Составьте логическую схему базы знаний по теме юниты:
- •2. Решите самостоятельно следующие задачи (номер варианта совпадает с Вашим номе-ром в списке группы):
- •Тренинг компетенций
- •1 Компетенция №1. Вычисление собственных значений и собственных векторов матрицы a порядка n
- •1.1 Пример решения типовой задачи
- •Глоссарий
- •Линейная алгебра юнита 4
Задания для самостоятельной работы
1. Составьте логическую схему базы знаний по теме юниты:
2. Решите самостоятельно следующие задачи (номер варианта совпадает с Вашим номе-ром в списке группы):
Задача № 1. Найти собственные значения и собственные векторы матрицы A:
Варианты:
№ 1
 № 2
№ 2
 № 3
№ 3

№ 4
 №
5
№
5
 № 6
№ 6

№ 7
 № 8
№ 8
 № 9
№ 9

№ 10
 № 11
№ 11
 № 12
№ 12
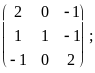
№ 13
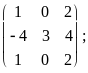 № 14
№ 14
 № 15
№ 15

№ 16
 № 17
№ 18
№ 17
№ 18
№ 19 № 20 № 21
№ 22
 № 23
№ 24
№ 23
№ 24

№ 25 № 26 № 27
№ 28
№ 29
№ 30
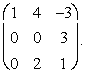
Задача № 2. Привести кривую второго порядка к каноническому виду ортогональным преоб-разованием.
Варианты:
№ 1. 4xy – x2 – y2 + 3 = 0.
№ 2. 2x2 + 2y2 – 2xy – 9 = 0.
№ 3. xy = 4.
№ 4. 2xy – 2x2 – 2y2 + 9 = 0.
№ 5. 4xy – 3x2 – 3y2 + 25 = 0.
№ 6. 15 – x2 – y2 – 4xy = 0.
№ 7. 6xy – 5x2 – 5y2 + 16 = 0.
№ 8. xy – 8 = 0.
№ 9. 3x2 + 3y2 – 4xy – 10 = 0.
№ 10. x2 + y2 – 8xy – 15 = 0.
№ 11. 5x2 + 5y2 – 2xy – 24 = 0.
№ 12. 4xy + 1 = 0.
№ 13. 2x2 + 2y2 – 2xy – 1 = 0.
№ 14. 3x2 + y2 – 4xy = 0.
№ 15. x2 + y2 + xy – 9 = 0.
№ 16. xy – 8 = 0.
№ 17. 4xy – x2 – y2 + 3 = 0.
№ 18. 3x2 + 3y2 – 4xy – 10 = 0.
№ 19. 2x2 + 2y2 – 2xy – 9 = 0.
№ 20. x2 + y2 – 8xy – 15 = 0.
№ 21. xy – 4 = 0.
№ 22. 5x2 + 5y2 – 2xy – 24 = 0.
№ 23. 2xy – 2x2 – 2y2 + 9 = 0.
№ 24. 4xy + 1 = 0.
№ 25. 4xy – 3x2 – 3y2 + 25 = 0.
№ 26. x2 + y2 = 0.
№ 27. 15 – x2 – y2 – 4xy = 0.
№ 28. 3x2 + y2 – 4xy = 0.
№ 29. 6xy – 5x2 – 5y2 + 16 = 0.
№ 30. x2 + y2 + xy – 9 = 0.
Задача № 3. При каких значениях параметра квадратичная форма Q(x) положительно опре-делена (указать ближайшее целое ).
Варианты:
№ 1.
![]()
№ 2.
![]()
№ 3.
![]()
№ 4.
![]()
№ 5.
![]()
№ 6.
![]()
№ 7.
![]()
№ 8.
![]()
№ 9.
![]()
№ 10.
![]()
№ 11.
![]()
№ 12.
![]()
№ 13.
![]()
№ 14.
![]()
№ 15.
![]()
№ 16.
![]()
№ 17.
№ 18.
![]()
№ 19.
№ 20.
№ 21.
![]()
№ 22.
№ 23.
№ 24.
№ 25.
№ 26.
№ 27.
№ 28.
№ 29.
![]()
№ 30.
![]()
Задача № 4. Определить координаты образа A(x), если задан вектор x и матрица A линейного преобразования A : R3 R3.
Варианты:
№ 1,
№ 16
 ;
№ 2, № 17
;
№ 2, № 17
 ;
;
№ 3,
№ 18
 ;
№ 4, № 19
;
№ 4, № 19
 ;
;
№ 5,
№ 20
 ;
№ 6, №
21
;
№ 6, №
21
 ;
;
№ 7,
№ 22
 ;
№ 8, № 23
;
№ 8, № 23
 ;
;
№ 9,
№ 24
 ;
№ 10, № 25
;
№ 10, № 25
 ;
;
№ 11,
№ 26
 ;
№ 12, № 27
;
№ 12, № 27
 ;
;
№ 13,
№ 28
 ;
№ 14, № 29
;
№ 14, № 29
 ;
;
№ 15,
№ 30
 .
.
Задача № 5. В пространстве V многочленов P(t) степени n2 со стандартным базисом e1 = 1, e2 = t, e3 = t2 задана система векторов f1, f2, f3 и оператор A : VV;
1) проверить, что f1, f2, f3 является тоже базисом;
2) проверить линейность оператора А;
3) найти матрицу перехода С от базиса {e} к базису {f};
4) найти матрицы Ae, Af оператора A в обоих базисах;
5) проверить формулу Af = C–1AeC.
Варианты:
№ 1, 16. f1 = 1 + t; f2 = t + t2; f3 = 1 + t2; A(p) = t p.
№ 2, 17. f1 = 1 + t; f2 = t + t2; f3 = 1 + t2; A(p) = p + p.
№ 3, 18. f1 = 1 + t; f2 = t + t2; f3 = 1 + t2; A(p) = 2p – p.
№ 4, 19. f1 = 1 ; f2 = 1 + t; f3 = 1 + t + t2; A(p) = t p.
№ 5, 20. f1 = 1; f2 = 1 + t; f3 = 1 + t + t2; A(p) = p + p.
№ 6, 21. f1 = 1; f2 = 1 + t; f3 = 1 + t + t2; A(p) = 2p – p.
№ 7, 22. f1 = 1 – t; f2 = t – t2; f3 = t2; A(p) = t p.
№ 8, 23. f1 = 1 – t; f2 = t – t2; f3 = t2; A(p) = p + p.
№ 9, 24. f1 = 1 – t; f2 = t – t2; f3 = t2; A(p) = 2p – p.
№ 10, 25. f1 = t(1 + t); f2 = t(t –1); f3 = 1; A(p) = t p.
№ 11, 26. f1 = t(1 + t); f2 = t(t –1); f3 = 1; A(p) = p + p.
№ 12, 27. f1 = t(1 + t); f2 = t(t –1); f3 = 1; A(p) = 2p – p.
№ 13, 28. f1 = t2 + t + 1; f2 = t2 + t; f3 = t2; A(p) = t p.
№ 14, 29. f1 = t2 + t + 1; f2 = t2 + t; f3 = t2; A(p) = p + p.
№ 15, 30. f1 = t2 + t + 1; f2 = t2 + t; f3 = t2; A(p) = 2p – p.
