Приложение 1 Перпендикуляр из точки на пространство

Задача о наилучшем приближении

Если вектор xR ортогонален векторам y₁,y₂,…,y_k, то очевидно, он ортогонален любому вектору из линейной оболочки L(y₁,y₂,…,y_k). Вообще, если R₁ – подпространство евклидова прост-ранства R, а вектор xR ортогонален любому вектору из R₁, то говорят, что вектор х ортогонален подпространству R₁. Совокупность всех таких векторов х, которые ортогональны подпро-странству R₁, сами образуют подпространство R₂. Его называют ортогональным дополнением к подпространству R₁.

Для того чтобы xR был ортогонален подпространству R₁, достаточно, чтобы х был ортого-нален каждому из векторов базиса R₁.

Заметим, что каждый вектор пространства xR может быть разложен на сумму 2-х векторов: х из подпространства R₁ и х из его ортогонального дополнения R₂. Размерность же всего прост-ранства есть прямая сумма размерностей подпространства и его ортогонального дополнения.

Рассмотрим в пространстве R некоторое m-мерное подпространство R₁: пусть вектор fR не принадлежит R₁. Поставим задачу: найти такой вектор f₀R₁, чтобы вектор h=f–f₀ был ортого-нален R₁. Вектор f₀ называют ортогональной проекцией f₁ на R₁ (см. рисунок, где в качестве R взято R³, а подпространство R₁ – произвольная плоскость; вектор f не лежит на плоскости R₁). Покажем сначала, что, как и в элементарной геометрии, перпендикуляр h есть кратчайшее расстоя-ние от точки f до подпространства R₁, т.е. если взять любой отличный от f₀ вектор f₁R₁, то

Действительно, так как f₀R₁ и f₁R₁, то и вектор f₀–f₁ R₁, а значит, ортогонален вектору h=f–f₀.

Используем теорему Пифагора:

.

Отсюда

Вычислим теперь по вектору f его ортогональную проекцию f₀ на подпространство R₁. Пусть e₁,e₂,…,e_m базис R₁, тогда f₀ можно искать в виде

f₀=c₁e₁ + c₂e₂ + … + c_me_m.

Коэффициенты c_i найдем, используя условия ортогональности f – f₀ = h к R₁. Для этого необ-ходимо и достаточно, чтобы

(h,e_i)=0; (f–f₀, e_i) = 0, (f, e_i) = (f₀,e_i) (i=1,2,…,m).

Подставляя вместо f₀ его выражение через векторы базиса, получим относительно c_i (i=1,2,…,m) систему уравнений:

(f, e_i) = c₁(e₁,e_i) + c₂(e₂,e_i) + … + c_m(e_m,e_i) (i=1,…,m) (*)

Если базис e₁,e₂,…,e_m – ортогональный и нормированный, то коэффициенты c_i получатся осо-бенно просто

c_i = (f,e_i) (i=1,…,m).

Система уравнений (*) позволяет однозначно вычислить в этом случае коэффициенты c_i, а значит однозначно найти проекцию вектора f на R₁.

Этот единственный вектор f₀ может быть вычислен и в том случае, если базис e₁,e₂,…,e_m – произвольный. Система уравнений (*) должна иметь единственное решение. Напомним, что это значит, определитель системы должен быть отличен от нуля:

.

Определитель G называют определителем Грама векторов e₁,e₂,…,e_m.

Итак, чтобы найти ортогональную проекцию f₀ вектора f₁ R₁ на подпространство R₁, следует координаты f₀ вычислить, решив систему уравнений (*). Если в R₁ выбран ортогональный норми-рованный базис e₁,e₂,…,e_m, то координаты f₀ вычисляются по формуле:

c_i = (f,e_i) (i = 1, 2, …, m).

Сформулируем еще одну полезную теорему об определителе Грама (доказательство ее опустим).

Теорема. Обозначим определитель Грама векторов x₁, x₂, …, x_m

.

Тогда выполняются неравенства

.

Причем знак равенства слева достигается только когда вектора x₁,…,x_m – линейно зависимы, а справа в случае попарной ортогональности векторов.

Рассмотрим примеры нахождения ортогональной проекции вектора на подпространство.

1. Метод наименьших квадратов.

Предполагается, что у есть линейная комбинация x₁, x₂,…,x_m с неизвестным коэффициентами .

.

Часто приходится определять c₁,…,c_m экспериментально, для чего n раз измеряются величины x₁,x₂,…,x_m и y.

Обозначим результаты k-го измерения x_1k,x_2k,…,x_mk и y_k соответственно (k=1,2,…,n). Тогда для определения чисел c₁,c₂,…,c_m получим систему

. (**)

Обычно n>m. Так как измерения величин x₁, …, x_m, y связано с погрешностями, то система (**), вообще говоря, несовместна, и можно говорить только о ее приближенном решении. “Лучшим” считается такой набор c₁,c₂,…,c_m, при котором достигается минимум квадратичного уклонения

.

Применим к этой задаче изложенные выше результаты. Рассмотрим n-мерное евклидово про-странство и векторы

e₁(x₁₁,x₁₂,…,x_1n), e₂(x₂₁,x₂₂,…,x_2n), …, e_m(x_m1,x_m2,…,x_mn).

Координаты вектора е_i – это результаты n-кратного измерения переменной x_i. Вектора e₁,e₂,…,e_m можно считать линейно независимыми; рассмотрим также вектор

y = (y₁,y₂,…y_m).

Систему уравнений (**) в векторном виде можно записать

c₁e₁ + c₂e₂ + … + c_me_m = y.

Выражение S есть квадрат длины вектора-разности

c₁e₁ + c₂e₂ + … + c_me_m – y.

Если обозначить R₁ – подпространство линейных комбинаций e₁,e₂,…,e_m, то задача сводится к нахождению ортогональной проекции вектора y на R₁, только в этом случае S достигает минимума.

Как было показано, числа c₁,c₂,…,c_m следует найти из системы уравнений (*) (f = y)

,

где

.

Упражнение.

Решить несовместную систему уравнений методом наименьших квадратов

3x₁–x₂=1

x₁+x₂ =0

4x₁ =–1

2. Приближение функции тригонометрическими полиномами. Пусть f(t) – непрерывная функ-ция на отрезке [0,2]. Ставится задача подобрать тригонометрический многочлен P(t) данного порядка, наименее отклоняющийся от f(t). За меру отклонения P(t) от функции f(t) берется квадра-тичное уклонение

.

Многочлен P(t) порядка n имеет вид

.

Напомним, что в пространстве непрерывных функций С_(0,2)скалярное произведение двух векторов f(t) и g(t) задается интегралом

.

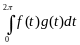Тогда S определяет квадрат расстояния от f(t) до P(t), т.е. квадрат длины вектора (f(t)–P(t)),

.

Чтобы минимизировать интеграл снова нужно из точки f(t) опустить перпендикуляр на подпространство R₁, натянутое на базис, состоящий из (2n+1) функции

.

Заметим, что базис {е} – ортогональный и нормированный. Тогда решением будет многочлен P(t),

где c_k = (f,e_k), k=0,1,…,2n.

Используя определение скалярного произведения в , получим

.