4.6 Евклидовы пространства

Определение евклидова пространства. С помощью понятия линейного пространства можно сформулировать, что такое прямая линия, плоскость, размерность пространства, параллельность. Однако многие факты евклидовой геометрии, связанные с измерением длин и углов, оставались за пределами наших рассмотрений. Вспомним, что в аналитической геометрии для определения длин и измерения углов между векторами можно было пользоваться понятием скалярного произведения. Но уже это понятие включало в себя умение мерить длину векторов и косинус угла. В арифми-тическом линейном пространстве было определено скалярное произведение, и с его помощью вводились основные метрические понятия (длина вектора, ортогональность векторов).

В общем линейном пространстве V введем понятие скалярного произведения аксиоматически.

Определение. Говорят, что в вещественном линейном пространстве V определено скалярное произведение, если каждой паре векторов поставлено в соответствие действительное число, которое обозначим , причем это соответствие удовлетворяет следующим аксиомам:

1. , т.е. скалярное произведение симметрично; (выполнен переместительный закон).

2. (распределительный закон).

3. , для любого вещественного .

4. при и при .

Таким образом, скалярное произведение векторов х и у является билинейной симметричной формой, положительно определенной. Всякая форма, обладающая этими свойствами, может быть принята за скалярное произведение.

Линейное пространство, в котором введено скалярное произведение, называется евкли-довым.

Примеры.

1. В трехмерном пространстве свободных векторов скалярное произведение двух векторов определяется как произведение их длин на косинус угла между ними. Аксиомы 1 – 4 выражают собой основные свойства скалярного произведения и доказываются в векторной алгебре.

2. В пространстве вводилось скалярное произведение двух векторов и по формуле

.

Легко проверить, что требования 1 – 4 выполняются.

3. В пространстве непрерывных на отрезке функций введем скалярное произведение двух функций и по формуле . Используя правила интегрирования, можно проверить, что аксиомы 1 – 4 выполняются.

Пусть V произвольное конечномерное евклидово пространство с базисом . Пусть и

,

.

Тогда, используя аксиомы 2 и 3, получим

.

Обозначим , где (аксиома 4). Получим общий вид скалярного произведения в конечном евклидовом пространстве

.

Задавая различным образом скалярное произведения базисных векторов , получим раз-личные формы скалярного произведения в V.

Основные метрические понятия. Определим теперь с помощью скалярного произведения длину вектора и угол между векторами.

1. Длина вектора.

Длиной вектора х, или нормой вектора в евклидовом пространстве будем называть величину

(берется арифметическое значение корня).

Заметим, что в пространствах и норма совпадает с обычной длиной вектора х. В пространстве для вектора

.

Нормой функции является величина . Эту величину обозначают иногда . Из определения нормы следует, что при , и при .

Абсолютную величину числового множителя можно выносить за знак нормы вектора

.

Вектор х, имеющий длину 1, называется нормированным. Очевидно, всякий ненулевой вектор х можно нормировать. Для этого достаточно умножить его на число ,

.

Множество называется ограниченным, если длины всех векторов ограничены фиксированной константой. Например, единичный шар пространства V – совокупность всех векторов , .

2. Угол между векторами.

Углом между парой векторов х, у будем называть тот угол , косинус которого равен отношению .

В пространствах и это согласуется с обычным выражением угла между векторами. Чтобы введенное понятие имело смысл в любом евклидном пространстве R, нужно доказать, что

,

т.е. что . Для доказательства рассмотрим вектор , где – вещественное число (аксиома 4)

.

Слева стоит квадратный трехчлен относительно , и т.к. он не отрицателен, его дискриминант

.

Отсюда , .

Неравенство называют неравенством Коши-Буняковского.

Посмотрим какой вид имеет неравенство Коши-Буняковского в различных пространствах.

1. В пространстве неравенство вытекает из определения скалярного произведения как длин векторов и косинуса угла между ними.

2. В пространстве неравенство Коши-Буняковского имеет вид

.

Оно справедливо для любой пары векторов и , т.е. для любых наборов чисел и .

3. В пространстве будем иметь

.

Например, найдем угол между функциями и в пространстве .

.

Так как интегралы

; ;

, то .

Угол же между функциями и в равен

,

т.к. интеграл от нечетной функции на симметричном интервале (1,-1) равен нулю. Таким образом, функции и ортогональны.

В пространстве две функции и считаются ортогональными, если .

Легко проверить, например, что любые два вектора из системы функций 1, , , , ,…, , взаимно ортогональны на отрезке . С помощью введенных понятий можно перенести на евклидовы пространства ряд теорем элементарной геометрии.

3. Теорема Пифагора и ее обобщение.

Пусть х и у ортогональные векторы, тогда естественно считать диагональю прямоуголь-ника со сторонами х и у. Покажем, что , т.е. что квадрат гипотенузы равен сумме квадратов катетов.

Действительно, по определению . Используя аксиомы 2, 1 и ортогональ-ность х и у, получим

,

что требовалось доказать.

Вообще, если взаимно ортогональны и , то . Если же х и у произвольные векторы, то по аналогии с элементарной геометрией – третья сторона треугольника, построенного на х и у. Используя неравенство Коши-Буняковского, получим

,

,

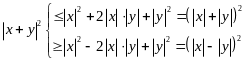т.е. длина любой стороны треугольника не больше, чем сумма длин двух других сторон и не меньше, чем модуль разности длин этих сторон.

.

Расстоянием между двумя точками х и у евклидова пространства называется длина вектора :

.

Ортогональный базис. В произвольном линейном пространстве не было оснований предпо-читать одни базисы другим, там все базисы были равноправны. В евклидовом пространстве суще-ствуют более удобные базисы – ортогональные; они играют здесь ту же роль, что и прямо-угольные системы координат в аналитической геометрии.

Мы докажем теперь теорему о существовании в произвольном евклидовом пространстве бази-са из взаимноортогональных векторов. Более того, нас будет интересовать ортогональный норми-рованный базис, т.е. такой базис , в котором векторы попарно ортогональны и имеют каждый единичную длину

. (*)

Докажем лемму.

Лемма 1. Взаимно ортогональные ненулевые векторы линейно независимы, т.е. что равенство

(**)

возможно лишь при .

Действительно, умножим обе части равенства (**) скалярно на . Получим:

.

Но по условию , , при . Следовательно . Аналогично, умножая (**) скалярно на получим .

Теорема. Во всяком n-мерном евклидовом пространстве существует ортогональный нормиро-ванный базис.

Мы уже подробно рассматривали, как строить ортогональную систему векторов в пространст-ве (процесс ортогонализации). Покажем для примера, как получить ортогональную систему функций в пространстве полинемов степени в .

Пусть . Будем искать . Из условия ортогональности и получаем . Потребуем, чтобы сумма коэффициентов многочлена равнялась единице (что равносильно равенству единице значения многочлена при t=1).

, , , .

Пусть теперь . Тогда

, и .

Отсюда получим , , , и .

Получили ортогональную систему полиномов:

, , .

Действуя аналогично, можем получить ортогональную систему многочленов степени при любом конечном n на отрезке .

Такую систему многочленов называют полиномами Лежандра. Полиномы Лежандра облада-ют многими замечательными свойствами и находят широкое применение в приложениях.

В евклидовом пространстве рассматривается задача о проекции произвольного вектора на некоторое подпространство W V и доказывается теорема о том, что каждый вектор может быть разложен в прямую сумму двух векторов, один из которых есть вектор подпространства W, а другой принадлежит ортогональному дополнению W. Подробнее об этой задаче можно прочесть в Приложении 1.