Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «мифи»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания
к выполнению индивидуальных заданий
по теме:
«Неопределенный интеграл. Определенный интеграл и его приложения»
Волгодонск
1. Неопределенный интеграл
Функция
называется первообразной функции
на некотором интервале
,
если
для всех значений
.
Если
-
первообразная
,
то очевидно, что бесконечное множество
всех первообразных
,
отличающихся
только константой,
также будет первообразной
.
Множество всех первообразных функций называется
неопределенным интегралом от функции и обозначается
.
При
этом
называется подынтегральной функцией,
подынтегральным выражением,
переменной интегрирования.
Согласно вышеприведенному
,
где
- некоторая
первообразная функции
;
– произвольная постоянная.
Неопределенный интеграл обладает следующими свойствами:
1.
.
2.
.
3.
,
где
.
4.
.
5.
.
Таблица основных неопределенных интегралов
1.
|
8.
|
2.
|
9.
|
3.
|
10.
|
4.
|
11.
|
5.
|
12.
|
6.
|
13.
|
7.
|
14. |
Основные методы интегрирования
1.1. Непосредственное интегрирование
Непосредственное интегрирование предполагает использование свойств неопределенного интеграла, таблицы интегралов и различных формул из элементарной математики.
Пример
1.
.
Решение: Воспользуемся свойствами 3-4 и формулой 1 таблицы интегралов:
Пример
2.
.
Решение:
Преобразуем
подынтегральную функцию:
.
Следовательно,
Пример
3.
.
Решение:
Так как
,
то
.
1.2. Метод подстановки
Mетод
подстановки (или замены переменной
интегрирования) заключается в том, что
заменяют переменную
на функцию
,
где
– непрерывно дифференцируемая функция,
т.е.
.
После
интегрирования возвращаются к старой
переменной обратной подстановкой:
.
Пример
1. Найти
.
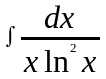Решение:
Пример
2. Найти
.
Решение.
Пример
3. Найти
.
Решение:
Пример
4. Найти
.
Решение:
Пример
5. Найти
.
Решение:
Пример
6. Найти
.
Решение:
1.3. Интегралы с квадратным трехчленом
Интегралы
с квадратным трехчленом - это интегралы
вида:
,
,
.
Для
вычисления этих интегралов необходимо
выделить в квадратных трехчленах
знаменателей полный квадрат. В первых
двух случаях квадратный трехчлен
перепишется в виде
,
в третьем он будет иметь вид
.
После замены
или
интегралы сводятся к одному или двум
табличным интегралам.
Замечание.
Если при
в квадратных трехчленах коэффициент
не равен 1, то его предварительно нужно
вынести за знак интеграла.
Пример
1. Найти
.
Решение:
=
=
=
=
=
=
=
Пример
2. Найти
Решение:
.
В первом интеграле сделаем замену:
=
Тогда исходный интеграл:
.
Пример3.
.
Решение:
=
=
.
В первом интеграле сделаем замену:
=
Тогда исходный приводится к виду:
( вернёмся к старым
переменным)=
=
=
.