2.3. Основные тождества и функции

АЛГЕБРЫ И ЛОГИКИ (ФАЛ)

В основе алгебры логики лежат три логические операции над такими переменными:

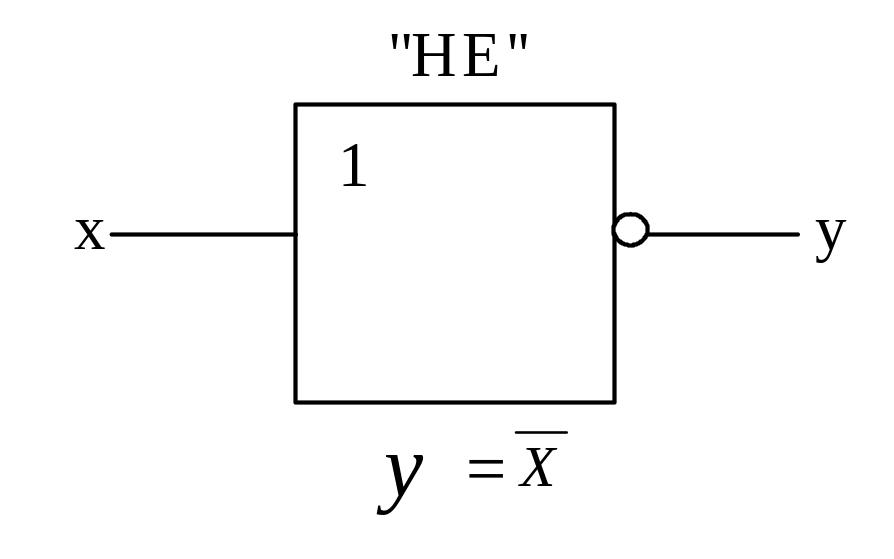
1. Инверсия (логическое отрицание) – обозначается чертой, которая ставится над переменной: ; читается НЕ Х.

2. Дизъюнкция (логическое сложение) – обозначается: Х₁ + Х₂ (для двух переменных); читается Х₁ или Х₂.

3. Конъюнкция (логическое умножение) – обозначается: Х₁  Х₂ (для двух переменных); читается Х₁ иХ₂.

Постулативно, предполагается, что при выполнении перечисленных операций отношения эквивалентности имеют вид:

ИЛИ И НЕ

0 + 0 = 0 0  0 = 0

1 + 0 = 1 1  0 = 0

0 + 1 = 1 0  1 = 0

1 + 1 = 1 1  1 = 1 = 0

На основании этих постулатов можно вывести основные тождества алгебры логики:

Х + 1 = 1; x  0 = 0;

Х + 0 = Х; x + = 1; ;

Х + Х = Х; Х  = 0; ;

Х  Х = Х; ;

Х  1 = Х; ;

;

Особое значение для синтеза КЦА, в случае необходимости использования данного базиса, имеют следующие тождества:

1. Распределительный закон:

;

2. Теорема Моргана (верна и в случае n – переменных):

а) ;

б) ;

в) ; (2.9)

г) ;

3. , доказываемое путем применения теоремы Моргана к правой или левой части.

Булевой функцией (или ФАЛ) называется двоичная переменная у, значение которой зависит от значений других двоичных переменных ( ), именуемых аргументами:

(2.10)

В этом выражении все переменные могут принимать одно из двух значений: 0 или1. Задание булевой функции означает, что каждому из возможных наборов (комбинаций) значений ее аргументов поставлено в соответствие определенное значение у. Поскольку каждый аргумент может принимать лишь одно из двух значений, то общее количество комбинаций Р из к двоичных аргументов составит:

; (2.11)

Возможные комбинации значений двух, трех, четырех входных аргументов имеют вид (таблица 2):

З

Таблица 2

N	X2	X1		N	X3	X2	X1		N	X4	X3	X2	X1
0 1 2 3	0 0 1 1	0 1 0 1		0 1 2 3 4 5 6 7	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1		0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1

десь удобно комбинации обозначать в виде представления десятичного числа N в двоичной системе счисления.

Скажем N = 12 = 1100.

В алгебре логики показано, что F - общее количество различных функций от к двоичных аргументов определяется выражением:

(2.12) Естественно, практическая реализация такого большого числа функций в виде логических элементов (микросхем) затруднительна. Можно показать, что существует система логических функций (набор логических элементов), позволяющая представить любую сколь угодно сложную функцию (построить сколь угодно сложный цифровой автомат). Такая система функций называется функционально полной системой логических функций, а набор логических элементов, ей соответствующий – функционально полным набором (ФПН).

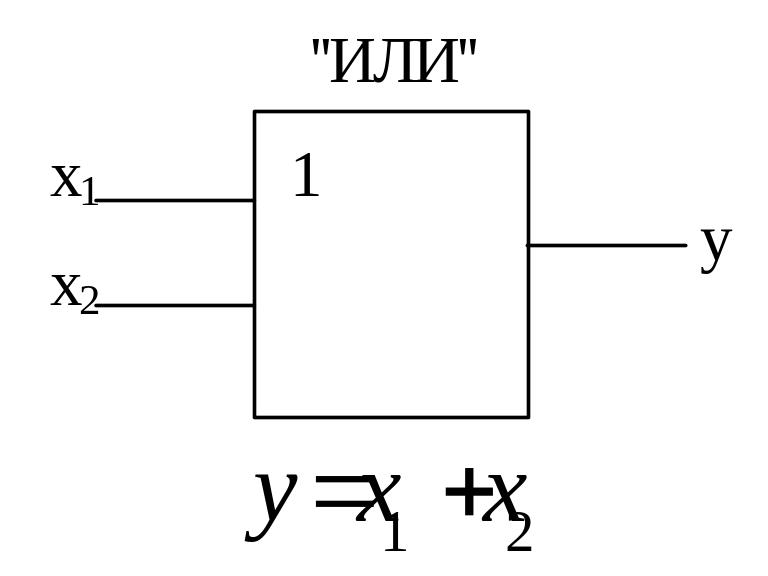
Один из возможных ФПН, схемотехническое обозначение логических элементов, и реализуемые логические функции приведены на рис.2 (для двух переменных).

И

рис.2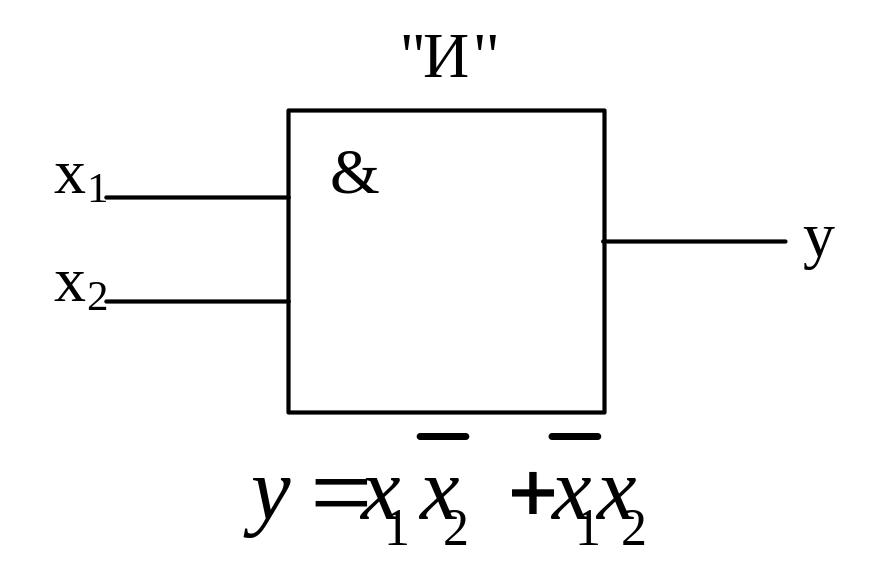

спользуя их суперпозицию можно построить любую логическую функцию. Например, функция неравнозначности двух аргументов имеет вид:

(2.13)

а устройство, реализующее ее, представлено на рис.3.

В

рис.3

составе современных серий интегральных микросхем имеются и другие ФПН, в виде так называемой двухступенчатой логики, когда один элемент выполняет последовательно две логические операции.

Э

''2 И-НЕ''

лемент Шеффера (И-НЕ), для двух переменных имеет вид:

Э

''2 ИЛИ-НЕ''

лемент Пирса (ИЛИ-НЕ), для переменных имеет вид:

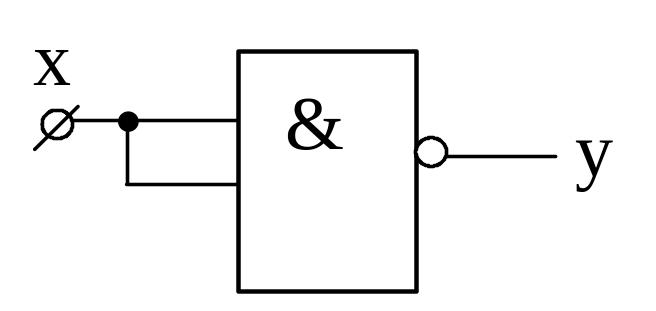
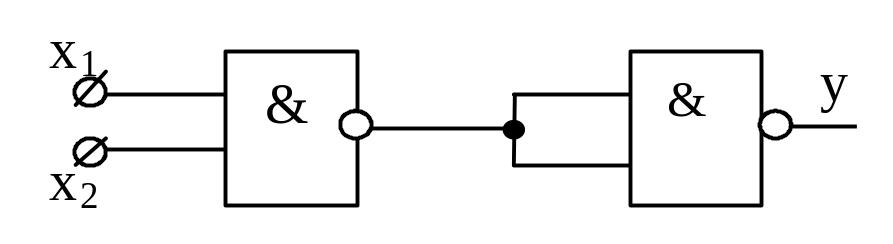
Для доказательства их функциональной полноты, покажем что из каждого из них можно получить базис (набор) И, ИЛИ, НЕ.

Результаты приведены в таблице 3.

На практике часто используются элементы многоступенчатой логики, выполняющие последовательно не две, а несколько операций.

НЕ	И	ИЛИ
		(следствие из т.Моргана)

таблица 3

Н

(2.14)

апример: микросхема К155ЛР3 (рис.4)

Н

(2.14.1)

апример: микросхема К155ЛП5 (рис.4.1)

Сравнивая (2.6) и (2.13) можно отметить их тождественность. Таким образом, сумматор по модулю 2 является цифровым дискрименатером, реагирующим на совпадение (неравнозначность) входных переменных.

Т.е. у = 1 тогда и только тогда x₁≠x₂ и y = 0, когда x₁=x₂