5. Обратная пропорциональность, ее свойства и график.

Определение. Обратной пропорциональностью называется функция, которую можно задать при помощи формулы вида , где х – независимая переменная, а К действительное число, не равно 0.

Число К называют коэффициентом обратной пропорциональности; К = у∙х.

Свойства обратной пропорциональности:

1. Область определения:

2. Множество значений:

3. Функция нечетная: f (-x) =- f(x).

Доказательство:

f (-x) = =- f(x).

График функции симметричен относительно начала координат.

Поэтому достаточно рассмотреть график обратной пропорциональности на интервале и отобразить его симметрично относительно точки (0;0).

4. На интервале функция:

а) при К > 0 – убывающая;

б) при К < 0 – возрастающая.

Доказательство:

Возьмем два различных значения аргумента х₁ и х₂ (х₂>х₁>0). Запишем соответствующие значения функции

Сравним у₁ и у₂:

Поскольку по условию х₁ < х₂ < 0, а х₁ ∙ х₂ > 0, то

а) если К > 0, то у₂ – у₁ < 0 у₂ < у₁, значит при К > 0 функция убывающая.

б) если К < 0, то у₂ – у₁ > 0 у₂ > у₁, значит при К < 0, функция возрастающая.

5. Основное свойство обратной пропорциональности: если задана обратная пропорциональность и две пары переменных (х₁; у₁) и (х₂; у₂), то имеет место равенство: или х₁ у₁ = х₂у₂ = К

Доказательство:

Если , то или х₁ у₁ = х₂у₂.

Из равенства или х₁ у₁ = х₂у₂ = К следует основное свойство обратной пропорциональности: две величины находятся в обратно пропорциональной зависимости, если с увеличением (уменьшением) в несколько раз одной из них вторая уменьшается (увеличивается) во столько же раз.

6. Графиком обратной пропорциональности является гипербола.

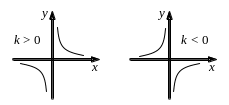
Примеры обратно пропорциональной зависимости.

– цена и количество товара при неизменной стоимости;

– длина основания и высота прямоугольника при постоянной площади и т.д.

С обратной пропорциональность учащиеся начальных классов встречаются, главным образом, при решении задач.

Задача. Надо упаковать в пакеты 24 кг муки. Какова будет масса 1 пакета, если эту муку упаковать в 3 одинаковых пакета? в 4 пакета?

В задаче рассматриваются три величины: масса муки в одном пакете, количество пакетов, масса всей муки. Масса всей муки – величина постоянная, ее значение 24. Две другие находятся в обратно пропорциональности зависимости, эту зависимость можно выразить формулой , где у – масса муки в одном пакете; х – количество пакетов.

Зная это, а) 24 : 3 = 8 (кг) муки в одном пакете;

б) 24 : 4 = 6 (кг) муки в одном пакете.

7