Тема. Функциональные отношения.

План.

1. Понятие функции

2. Способы задания функции

3. Линейная функция, ее свойства и график

4. Прямая пропорциональность, ее свойства и график

5. Обратная пропорциональность, ее свойства и график.

1. Понятие функции.

Определение. Соответсвие между элементами двух множеств, при котором каждому элементу первого множества соответствует не более одного элемента второго множества, называется функцией.

При этом, область определения соответствия называется областью определения функции, а область значений соответствия – областью значений функции.

Например, среди соответствий, изображенных на рисунке, функциями будут f, h и p. Их областями определения будут, соответственно, D(f) = {a, b, c}, D(h) = {a, c}, D(p) = {a, b, c}, а множествами значений E(f) = {1, 3}, E(h) = {1, 2}, E(p) = {1, 2, 3}.

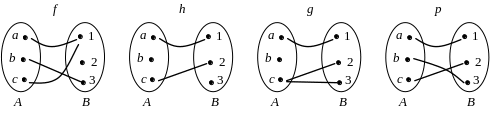
Рис. 1

Е сли и f — функциональное соответствие между элементами x и y, то записывают y = f(x) или . Элемент соответствующий элементу , называют значением функции, а элемент – аргументом.

Изучение функций в школьном курсе математики начинается в средних классах, но подготовка учащихся к усвоению этого важного в математике понятия начинается уже в начальных классах.

Функция, устанавливающая соответствие между двумя числовыми множествами называется числовой функцией.

Определение. Функция y = f(x) называется четной (нечетной), если в ее область определения вместе с любым элементом х входит противоположный ему элемент – х и выполняется равенство f (-x) = f(x) (f(-x) = -f(x)).

График четной (нечетной) функции симметричен относительно оси ОУ (начала координат).

Определение. Функция y = f(x) называется возрастающей (убывающей) на интервале (а;в), если для любых точек х₁ и х₂ из (а;в) из того, что х₁ < х₂ следует, что f (x₁) < f(x₂) (f(x₁) > f(x₂)).

Другими словами: функция y = f(x) называется возрастающей (убывающей) на интервале (а;в) если большему значению аргумента соответствует большее (меньшее) значение функции.

2. Способы задания функции

1) Аналитическое задание функции (задание функции формулой).

Этот способ задания функции наиболее распространен в математике. При аналитическом задании функции указывается формула, которая указывает совокупность операций, которые нужно выполнить, чтобы по заданному значению аргумента функции найти соответствующее значение функции. Одно и тоже числовое выражение может задавать различные функции в зависимости от того множества, на котором рассматривается это выражение.

2) Табличный способ задания функции.

В случае конечных множеств функцию можно задать с помощью графа или перечислением всех пар элементов, находящихся в данном отношении. При этом пары элементов можно записать в виде таблицы.

3) Графический способ задания функции.

Функция полностью определяется заданием пар (x; f(x)), где х пробегает все множество D(f), а y = f(x) — соответствующие значения функции — множество E(f). Множество этих пар можно записать так: Графиком функции y = f(x), называется множество пар (х,у) таких, что , а y = f(x). Если областью определения и множеством значений функции являются числовые множества, то каждой такой паре соответствует некоторая точка на координатной плоскости, имеющая координаты х (абсцисса) и f(x), (ордината).

Построив график отношения (произвольного), можно определить, является оно функцией или нет. Так, если каждой точке оси абсцисс соответствует не более одной точки оси ординат, то рассматриваемое отношение является функцией. Например, изображенное на рис. 2 (а) отношение является функцией, а отношение на рис. 2 (б) функцией не является, т.к. например, значению аргумента х₁ соответствует два значения отношения – у₁ и у₂.

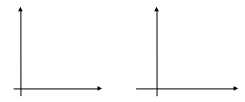
а) б)

Рис. 2

Сравнивая различные способы задания функции, легко установить, что недостатком аналитического способа задания функции является малая его наглядность, но по аналитическому заданию функции легко проводить ее исследование, используя математический аппарат. Часто сочетают аналитический и графический способы задания функций: по заданной формуле строится график.