Лекция 0. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ. РАСЧЕТ ПОГРЕШНОСТЕЙ.
Обратите внимание на стр. 9 – 11!!!
Измерением называется нахождение значения физической величины опытным путем с помощью специальных технических средств.
прямые (измерение диаметра проволоки штангенциркулем, измерение времени по секундомеру). Значение искомой величины находится из отсчета по прибору.
косвенные (определение плотности вещества по массе (измерена на весах) и объему (размеры измерены линейкой)). Значение искомой величины находится по формуле
Единичное измерение недопустимо!
При измерении находится не точное, а приближенное значение искомой физической величины, т.е. полученный результат содержит погрешность.
Источников погрешностей много: несовершенство приборов, наших органов чувств, влиянием внешних факторов, приближенный характер метода, округление при отсчетах и вычислениях и т.д.
Точные числа
ч
исловые
коэффициенты
,
Показатели степеней
Коэффициенты, отражающие дольность и кратность единиц измерения
1
с=
мин;
показатель преломления вакуума (точно) n=1
Кратные
Тера Т 1012 (т.е. 1 ТДж = 1.1012Дж)
Гига Г 109 (т.е. 1 ГОм = 1.109Ом)
Мега М 106 (т.е. 1МОм = 1.106Ом)
Кило К 103 (т.е. 1км = 1.103м)
Гекто г 102 (т.е. 1 гВт = 1.102Вт)
Дольные
Деци д 10-1 дециметр дм (10-1м)
Санти с 10-2 сантиметр см (10-2м)
Милли м 10-3 миллиметр мкм (10-3м)
Микро мк 10-6 микрометр мкм (10-6м)
Нано н 10-9 нанометр нм (10-9м)
П
огрешность
точных чисел равна нулю.
Все приближенные числа имеют отличную от нуля погрешность
Приближенные числа
результаты измерений;
округленные значения точных чисел
табличные значения мат., физ., хим. величин
иррациональные числа
; 
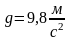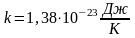
=3,14; 
; 
.
Значащие цифры (в точных и приближенных числах)
Все цифры и нули (не расположенные вначале числа) числа – значащие.
Пример: 3,1416 5 – значащих цифр
Пример: 5,094.105 4 - значащие цифры
Пример:
3 – значащие
цифры,
-
не относится к знач. цифрам
Пример: 0,0172 3 - значащие цифры
Необоснованное дописывание нулей в конце приближенного числа приводит к
увеличению значащих цифр в нем.
Пример:
1.
2.
90,0
см 0,900 м
(если
последует запись
,
то полностью утеряна информация о сотых
и тысячных долях метра. Уменьшено число
значащих цифр, понижена точность).
Потеря же нулей приводит к уменьшению точности числа.
Для точных чисел дополнительные нули возможны.
Нормальная форма записи числа: первая значащая в разряде единиц; остальные сохраняются; число записывается с множителем 10n (где n положительное или отрицательное целое).
Пример: 1,72.10-2 или 1,980.103
В такой форме записаны числа в справочных таблицах:
Гравитационная
постоянная G= 6,67·10-11
Нормальное атмосферное давление р0=1,01325.105Па
Универсальная
газовая R=8,31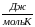
Верные, сомнительные и неверные цифры.
(только в приближенных числах)
В точных числах все цифры верные.
В приближенных числах количество верных определяется абсолютной погрешностью числа.
Пример.
140
51
(8
Содержащая (щие) погрешность цифры сомнительные.
Все цифры, стоящие после сомнительной неверные, отбрасываются с использованием правил округления и запасной цифры.
Пример:
40
21
Приближенные числа справочных таблиц
В числовых данных справочных таблиц принято записывать только верные.
Следовательно, - абсолютная погрешность ∆х данных справочных таблиц не превышает половины единицы последнего разряда.
Пример:
1.
Нд=13,6
103
В качестве
предельной абсолютной погрешности
,
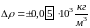тогда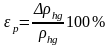
,
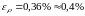
ч
исло
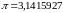
3,14 
3,142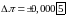 
Округление чисел
Распространяется на точные и приближенные числа
Пример: 7,192 7,19 7,2
1681 1,7.103
0,80214 0,80
Округление погрешностей и результатов измерений.
При Р=0,95 погрешность округляют до одной значащей цифры.
Пример:
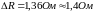
Исключение: если число содержит первую цифру 1, то сохраняется вторая сомнительная (значащая)
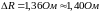! (для исключения грубой ошибки
при округлении)
Относительная погрешность также округляется.
Правильно округленная абсолютная погрешность позволяет правильно округлить и записать результат измерения, (содержащий верные и одну (две) сомнительные значащие цифры).
Пример:
,
Р=0,95
Р=0,95
Р=0,95
Число значащих цифр однозначно определяется погрешностью.