
- •1Основные теоретические положения и расчетные формулы.
- •1.1Извлечение корня n-ой степени из комплексного числа:
- •1.2Элементарные функции комплексного переменного:
- •1.3Кривые на комплексной плоскости.
- •1.4Дифференцирование функций комплексного переменного
- •1.5Интегрирование функций комплексного переменного
- •1.6Степенной ряд с комплексными числами
- •1.7Ряд Лорана
- •1.8Изолированные особые точки однозначной аналитической функции
- •1.9Вычеты
- •1.10Вычисление определенных интегралов от функций действительного переменного
- •1.11Конформные отображения
- •2Примеры выполнения типового расчета
- •3Домашнее задание по тфкп.
- •4Список литературы
2Примеры выполнения типового расчета
Задача 2.1. Найти все значения корня:
1.
![]() 2.
2.
![]()
Решение: 1.
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
2.
![]() ,
,
![]() ,
,
![]()
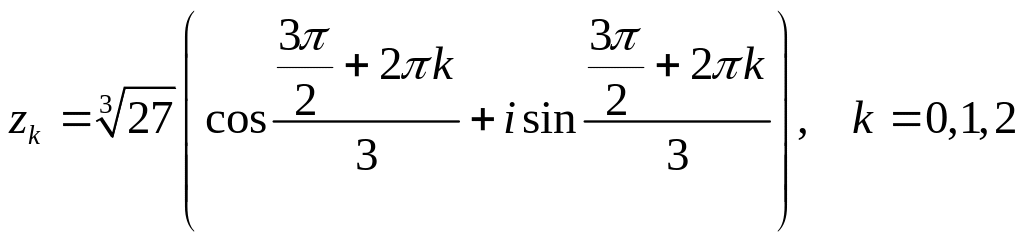
![]()
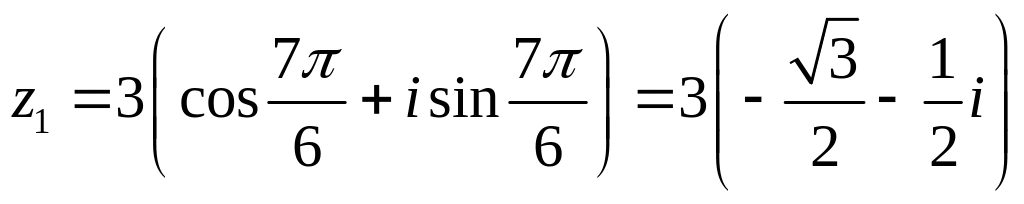
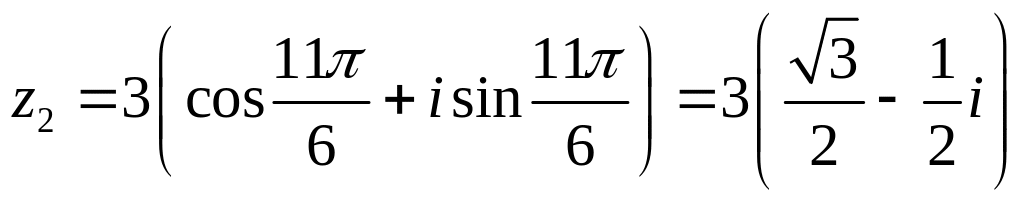
На комплексной плоскости значения корней могут быть представлены следующим образом (см. рис 2.1 и 2.2)
Задача 2.2. Представить в алгебраической форме:
1.
![]() ;
2.
;
2.
![]()
Решение:
1.
![]()
![]()
![]()
Т. о. - действительное число.
2.
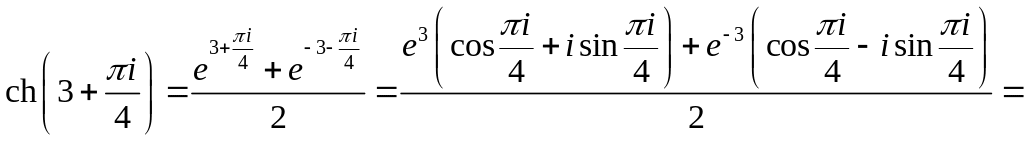
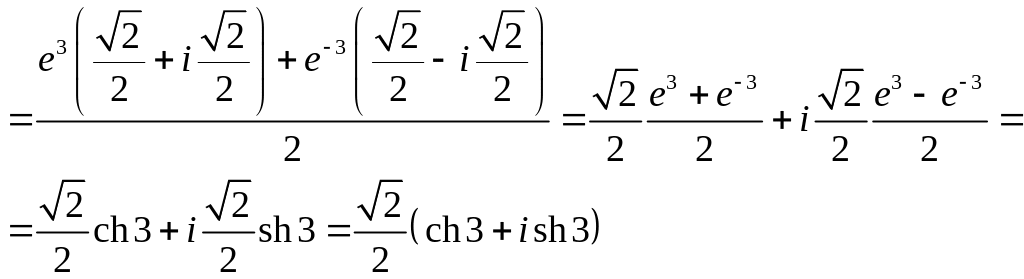
Задача 2.3. Представить в алгебраической форме:
1.
![]() 2.
2.
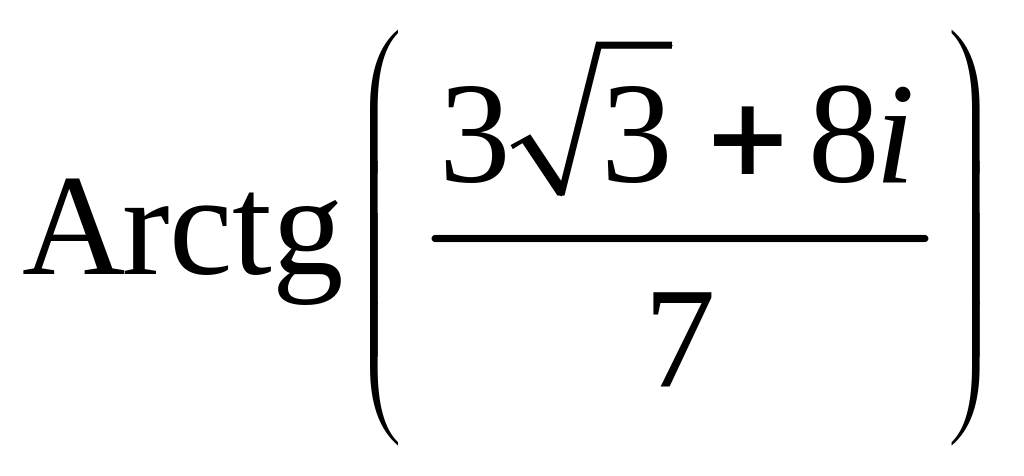
Решение:
1.
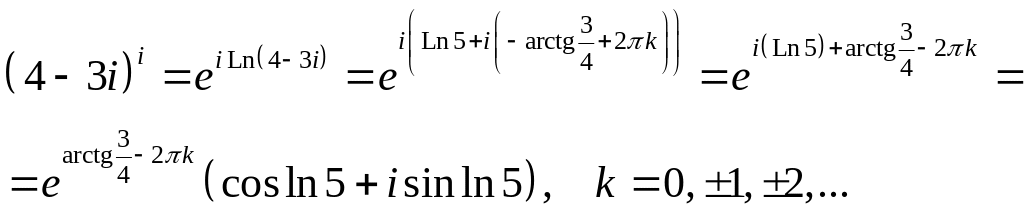
2.
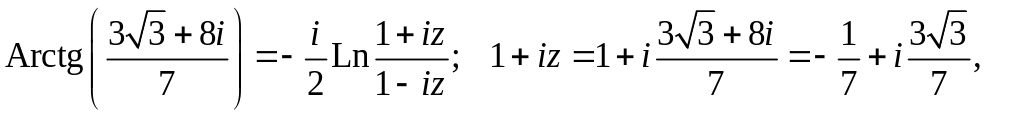
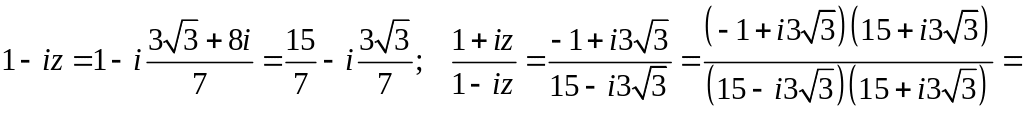
![]()
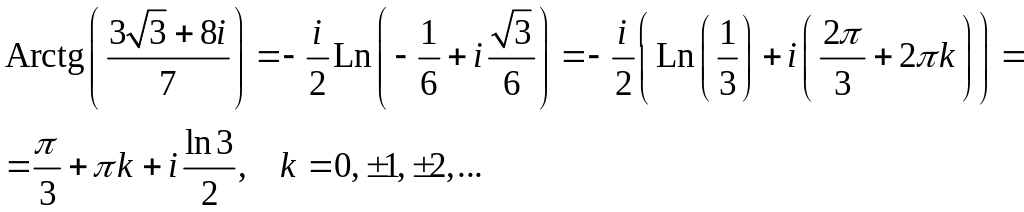
Задача 2.4.Вычертить область, заданную неравенствами:
1.
![]() ;
2.
;
2.
![]()
Решение:
![]() - кольцо, ограниченное
окружностями
- кольцо, ограниченное
окружностями
![]() ,
окружности не принадлежат области:
,
окружности не принадлежат области:
![]() правая полуплоскость
без границы;
правая полуплоскость
без границы;
![]() - полоса, ограниченная
прямыми
- полоса, ограниченная
прямыми
![]() и
и
![]() прямые принадлежат области. Таким
образом, на комплексной плоскости
область имеет вид(см.
рис 2.3):
прямые принадлежат области. Таким
образом, на комплексной плоскости
область имеет вид(см.
рис 2.3):
![]() - круг единичного
радиуса с центром в точке
- круг единичного
радиуса с центром в точке
![]() ,
граница круга области не принадлежит.
,
граница круга области не принадлежит.
![]() - полуплоскость,
расположенная выше прямой
- полуплоскость,
расположенная выше прямой
![]() вместе с границей;
вместе с границей;
![]() - полуплоскость,
расположенная ниже прямой
- полуплоскость,
расположенная ниже прямой
![]() вместе с границей.
вместе с границей.
Таким образом, область на комплексной плоскости имеет вид (см. рис 2.4):
Задача 2.5. Определить вид кривой:
1.
![]()
2.
![]()
Решение:
1.
![]()
![]() - прямая.
- прямая.
2.
![]()
![]()
Приведем уравнение к каноническому виду. Повернем координатные оси на угол .
![]()
![]()
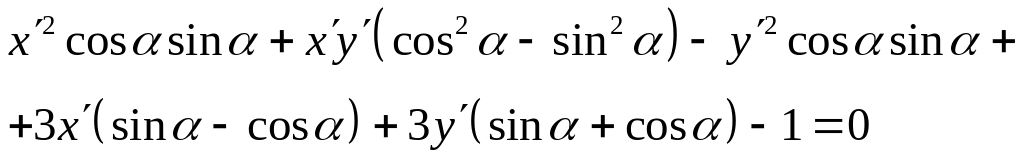
Угол
выберем так, чтобы
![]()
Тогда
![]()
Пусть
![]() .
Тогда
.
Тогда
![]() - гипербола.
- гипербола.
Задача 2.6. Восстановить
аналитическую в окрестности точки
функцию
по известной действительной части
![]() или мнимой части
или мнимой части
![]() и значению
и значению
![]() .
.
Решение. Проверим является ли функция гармонической.
![]()
Т.е. – гармоническая функция.
Потребуем выполнения условий Коши-Римана:
![]()
Из первого условия:
![]()
Из второго условия:
![]()
Следовательно,
![]() .Тогда
.Тогда
![]() или
или
![]()
Из условия
![]() имеем
имеем
![]() .
Таким образом,
.
Таким образом,
![]()
2. Проверим гармоничность функции :
![]()
- гармоническая функция.
Потребуем выполнения условий Коши-Римана:
Из первого условия:
![]()
Из второго условия:
![]()
Следовательно,
![]() .
Тогда
.
Тогда
![]() или
или
![]() .
Из условия
имеем
.
.
Из условия
имеем
.
Таким образом,
![]() .
.
Задача 2.7. Вычислить интеграл от функции комплексного переменного по данной кривой.
1.
![]()
2.
![]() ,
АВ – отрезок прямой,
,
АВ – отрезок прямой,
![]()
Решение 1. Кривая
![]() ,
вдоль которой ведется интегрирование,
представлена на рис 2.5.
,
вдоль которой ведется интегрирование,
представлена на рис 2.5.
Подынтегральная функция аналитическая, поэтому можно воспользоваться формулой Ньютона-Лейбница.
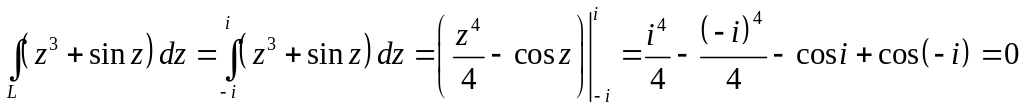
Отрезок АВ, вдоль которого ведется интегрирование, представлен на рис. 2.6.
![]()
![]()
Уравнение
прямой АВ
,
тогда вдоль АВ
![]() ,
,
![]()
.
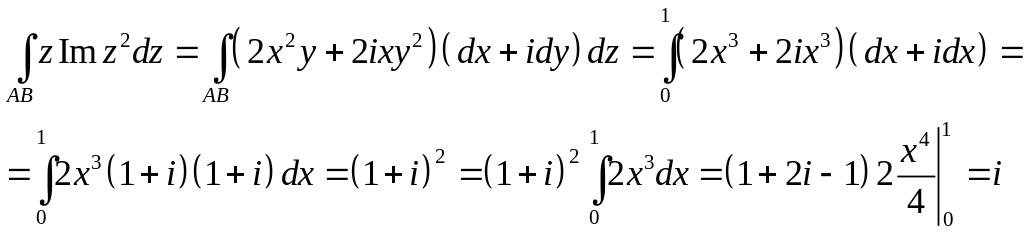
Задача 2.8. Найти все лорановские разложения данной функции по степеням :
1.
![]()
2.
![]()
Решение.
1. Разложим функцию на простые дроби.
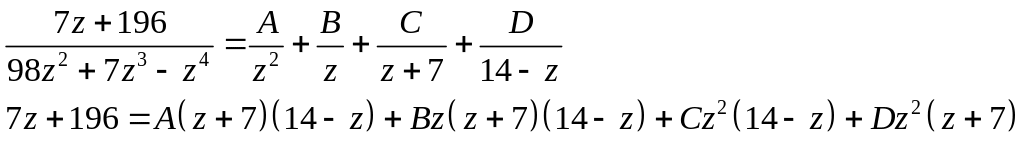
![]()
Приравнивая
коэффициенты при
![]() :
:
![]()
Тогда
![]()
Функция имеет следующие области аналитичности:
![]()
В области
![]()

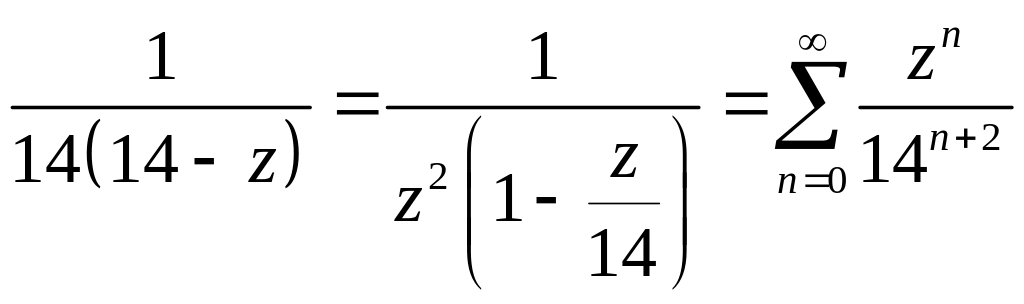
тогда
![]()
В области
![]()
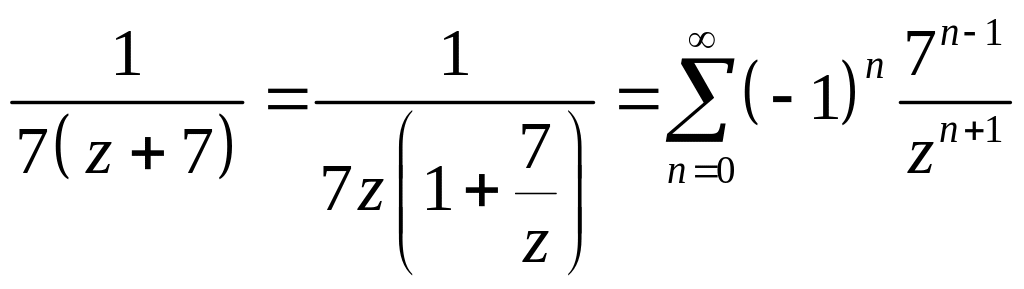
![]()
тогда
![]()
В области
![]()
![]()
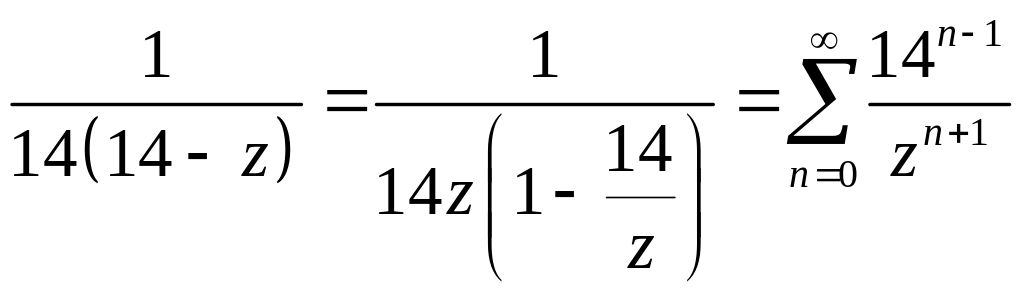
Тогда
![]()
2. Разложим функцию на простые дроби.
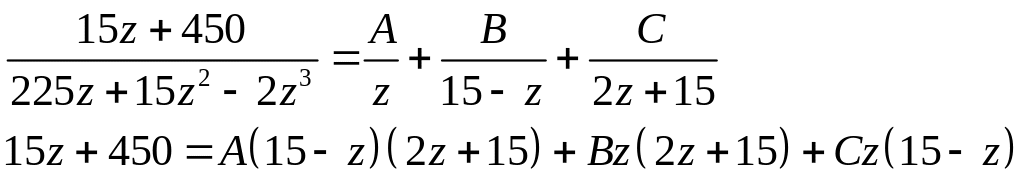
![]()
Тогда
![]()
Функция имеет следующие области аналитичности:
![]()
В области
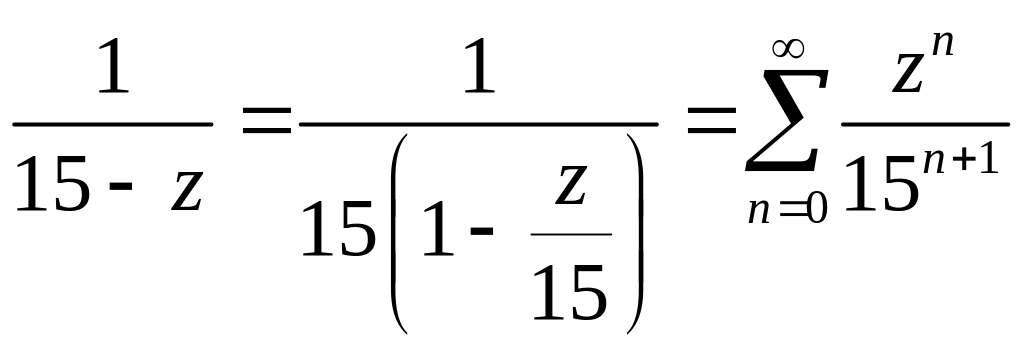
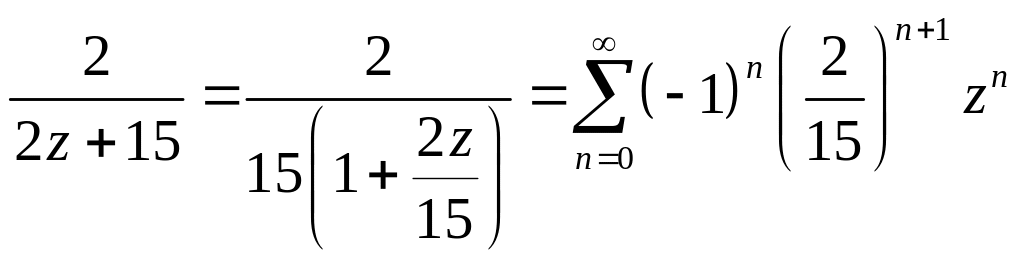
Тогда
![]()
В области .
![]()

Тогда
![]()
В области .
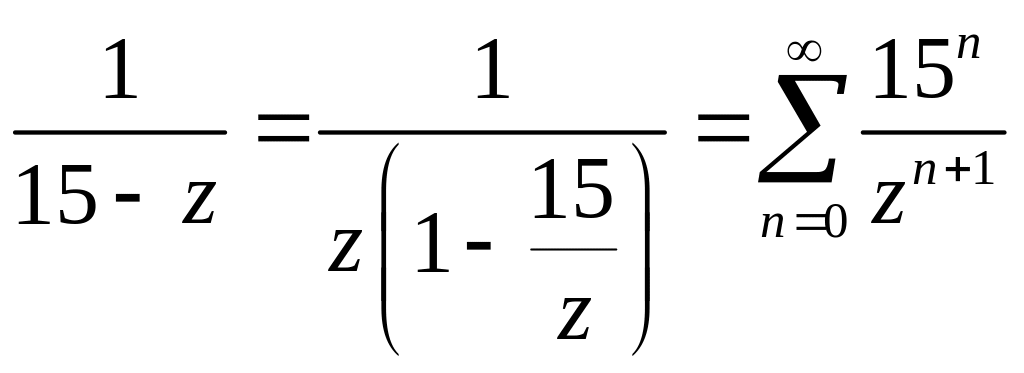
![]()
Тогда
![]()
Задача 2.9. Найти
все лорановские разложения данной
функции по степеням
![]() .
.
1.
![]()
2.
![]()
Решение. Так как
функция
аналитическая всюду, кроме точек
![]() ,
,
![]() и
и
![]() ,
,![]() ,
то она может быть разложена в ряд Лорана
по степеням
,
то она может быть разложена в ряд Лорана
по степеням
![]() в следующих областях:
в следующих областях:
![]()
Разложим на простые дроби
![]()
В области
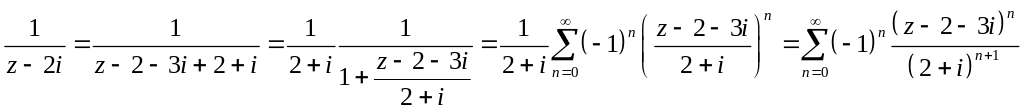
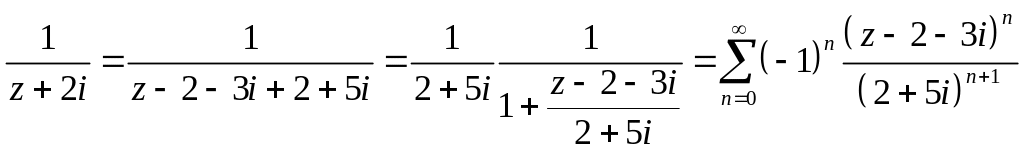
Тогда
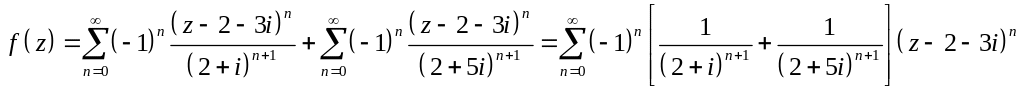 В
области
.
В
области
.
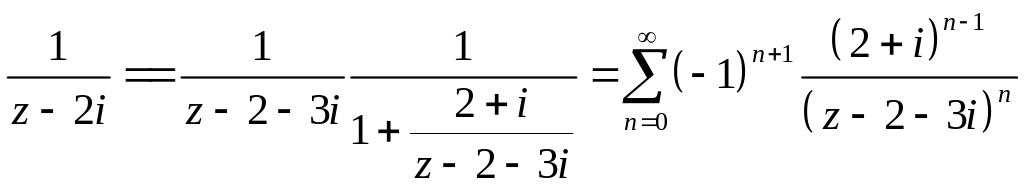

Тогда
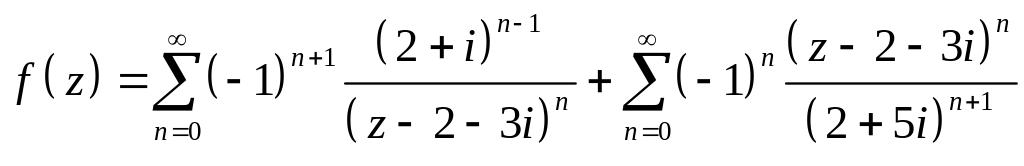
В области .
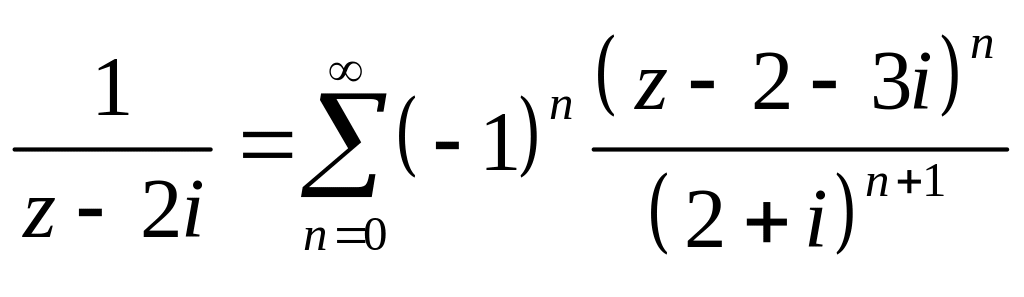
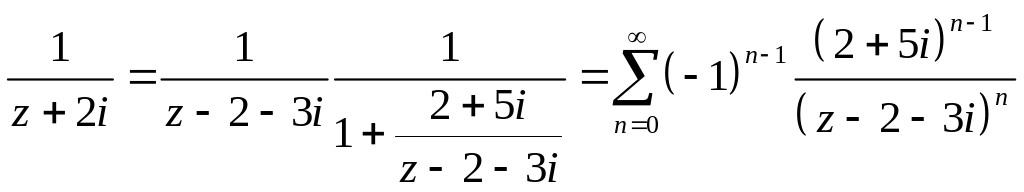
Тогда
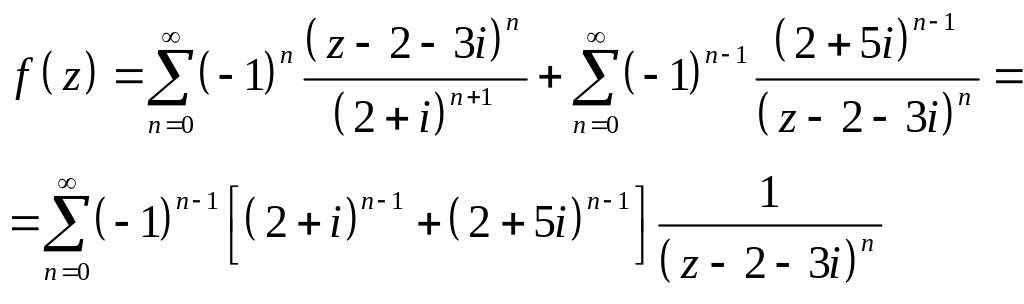
2. Так как
аналитическая всюду, кроме точек
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
то она может быть разложена в ряд Лорана
по степеням
,
то она может быть разложена в ряд Лорана
по степеням
![]() в следующих областях:
в следующих областях:
![]()
Разложим на простые дроби:
![]()
Если
![]() ,
то
,
то
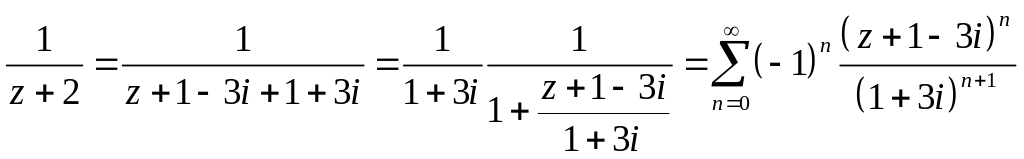
Если
![]() ,
то
,
то
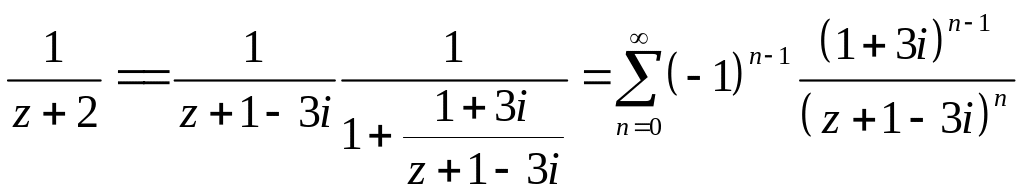
Если
![]() ,
то
,
то

Если
![]() ,
то
,
то

Тогда в области
:
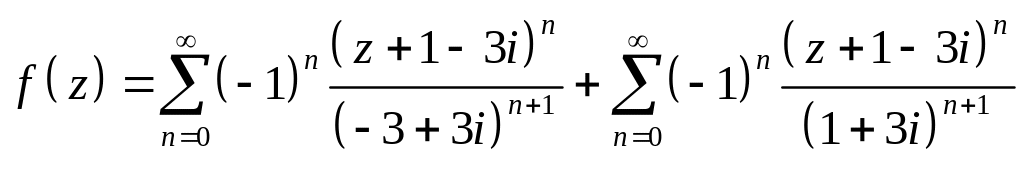 .
.
В области
:
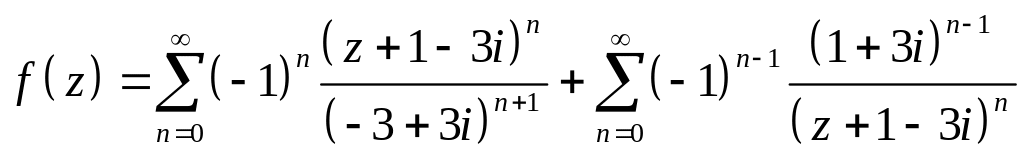 .
.
В области
:
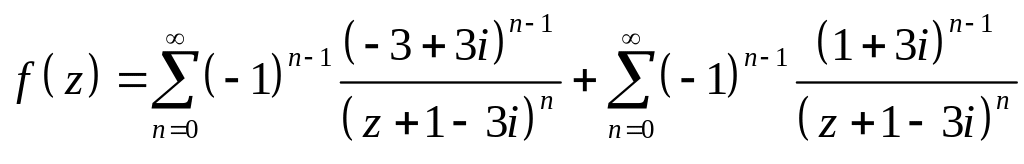 .
.
Задача 2.10. Данную функцию разложить в ряд Лорана в окрестности точки .
1.
![]()
2.
![]()
Решение.1. Функция
имеет одну особую точку
,
т.е. она является аналитической в области
![]() .
В этой области запишем ее разложение в
ряд Лорана, используя разложение функции
:
.
В этой области запишем ее разложение в
ряд Лорана, используя разложение функции
:
![]()
Тогда
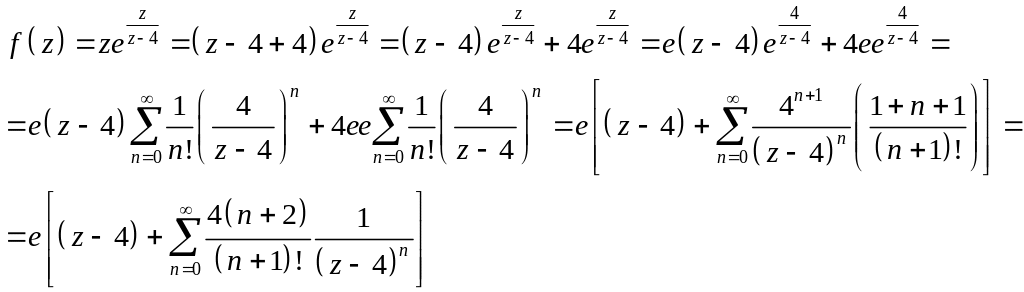
2. Функция имеет
одну особую точку
![]() ,
т.е. она является аналитической в области
,
т.е. она является аналитической в области
![]() .
В этой области запишем ее разложение в
ряд Лорана, используя разложение функции
.
В этой области запишем ее разложение в
ряд Лорана, используя разложение функции
![]() :
:

Тогда

Задача 2.11. Определить тип особой точки данной функции
1.
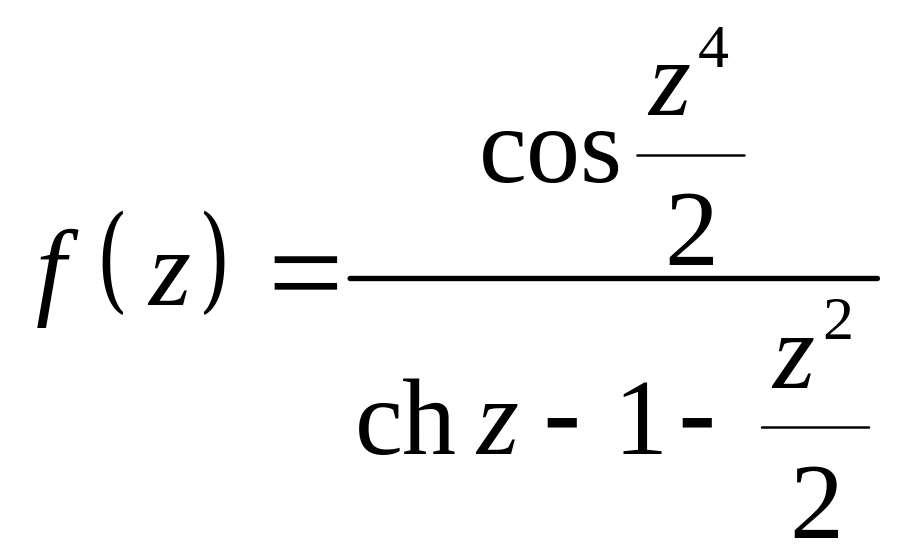
2.
![]()
Решение
 ,т.е точка
,т.е точка
![]() не является нулем числителя
не является нулем числителя
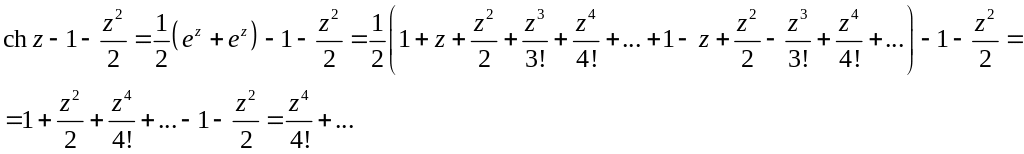 т.е
точка
является нулем 4-го порядка
т.е
точка
является нулем 4-го порядка
2.
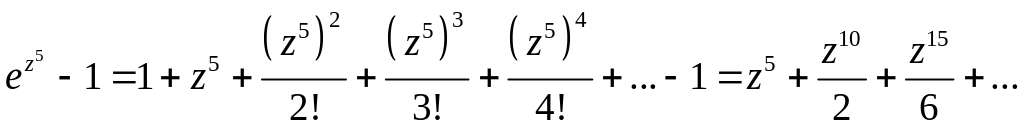
т.е. есть нуль 5-го порядка числителя
![]()
т.е. есть нуль 2-го порядка знаменателя. Это означает, что имеет в точке нуль 3-го порядка, т.е. есть устранимая особая точка функции.
Задача 2.12. Для заданной функции найти изолированные особые точки и определить их тип:
1.
![]()
2.
![]()
Решение 1.
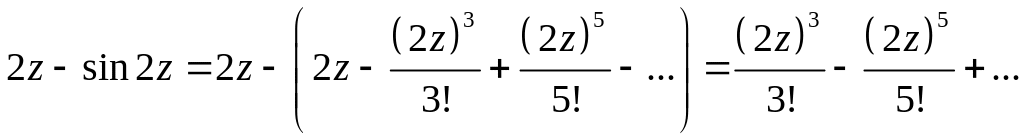
т.е. есть нуль 3-го порядка числителя.
Одновременно есть нуль 2-го порядка для знаменателя. Это означает, что есть нуль 1-го порядка , т. е. есть устранимая особая точка функции .
![]() ,
т.е.
,
т.е.
![]() есть
полюсы 1-го порядка
.
есть
полюсы 1-го порядка
.
2.
есть существенно особая точка функции
,
т. к. не существует предела
![]() .
.
![]()
![]()
т. е.
![]() есть устранимая особая точка функции
.
есть устранимая особая точка функции
.
![]()
т. е.
![]() есть устранимая особая точка функции
.
есть устранимая особая точка функции
.
есть полюсы 1-го порядка , т. к. они являются нулями 1-го порядка знаменателя и не являются нулями числителя.
Задача 2.13. Вычислить интегралы:
1.
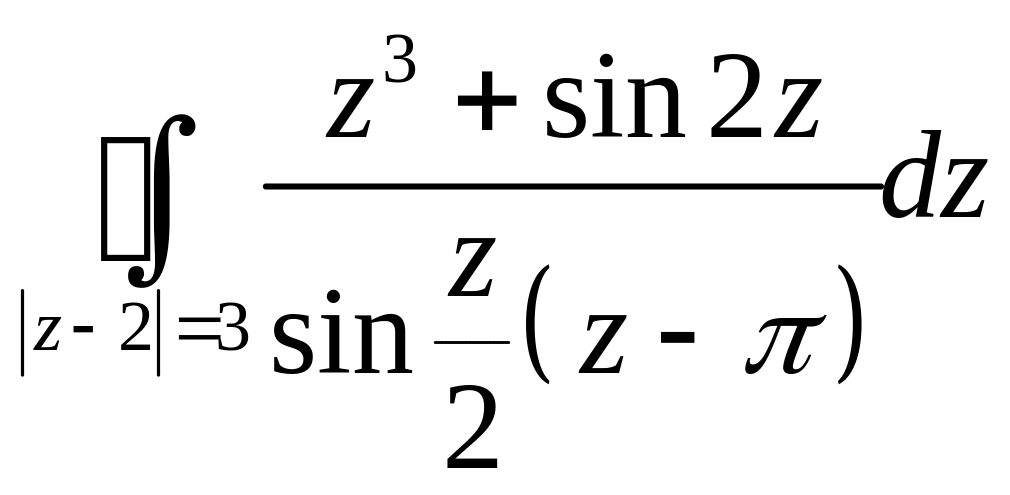 .
.
2.
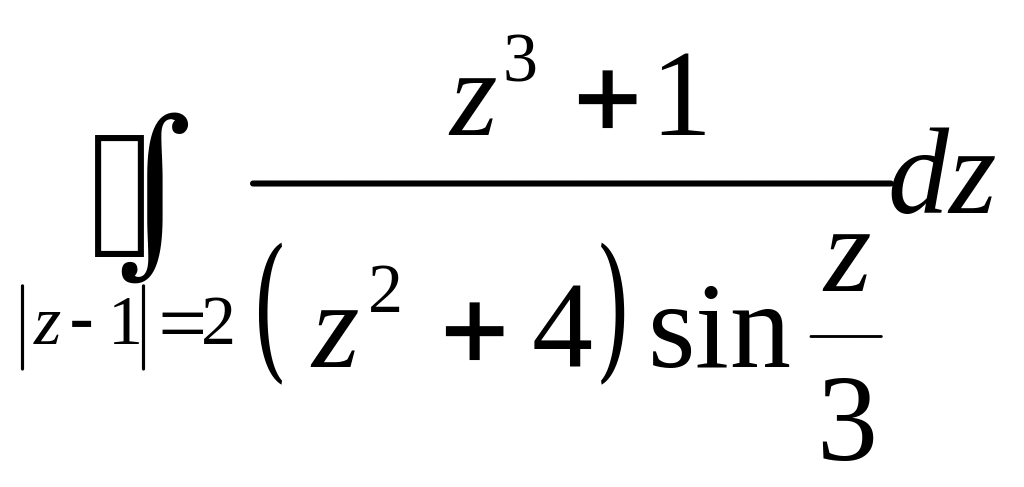
Решение.
1. Внутри контура
![]() имеет особые точки:
имеет особые точки:
- устранимая особая
точка, т.к.
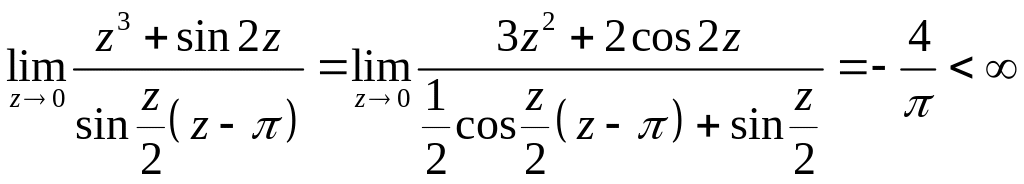
Вычет в точке равен 0.
![]() - полюс 1-го порядка.
- полюс 1-го порядка.
Вычет в точке равен
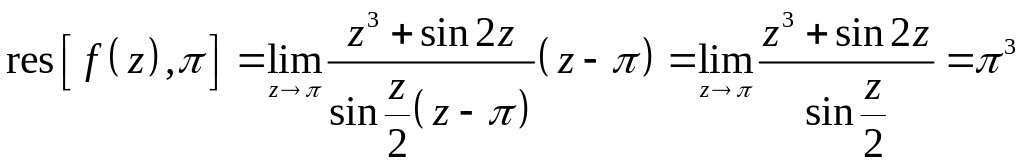
Тогда по основной теореме о вычетах
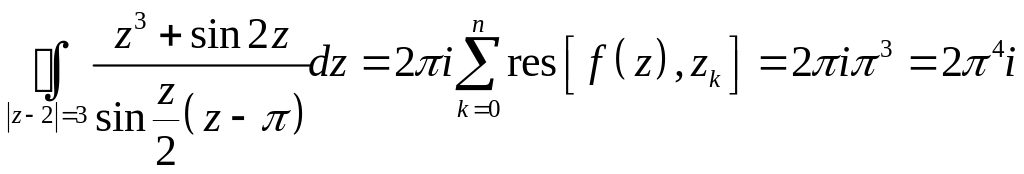
2. Внутри контура
![]() имеет особую точку
- полюс 1-го порядка
имеет особую точку
- полюс 1-го порядка
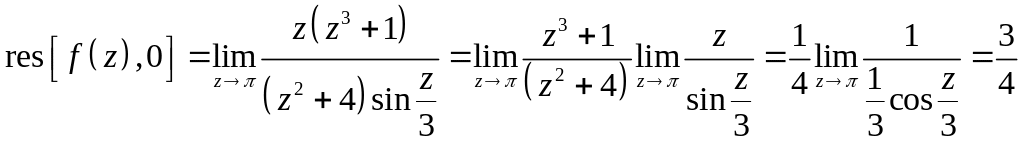
Тогда
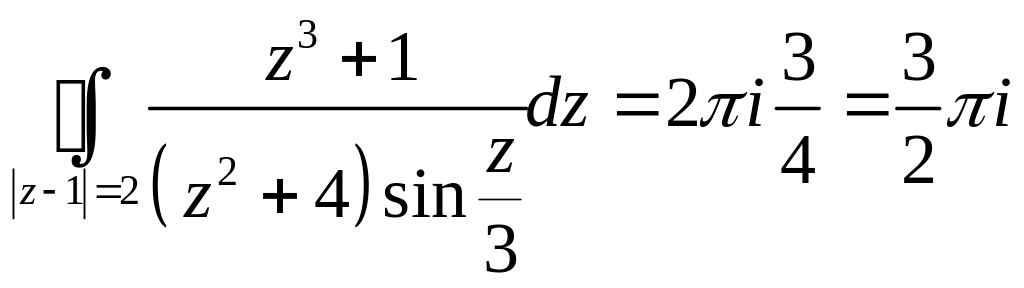
Задача 2.14. Вычислить интегралы:
1.
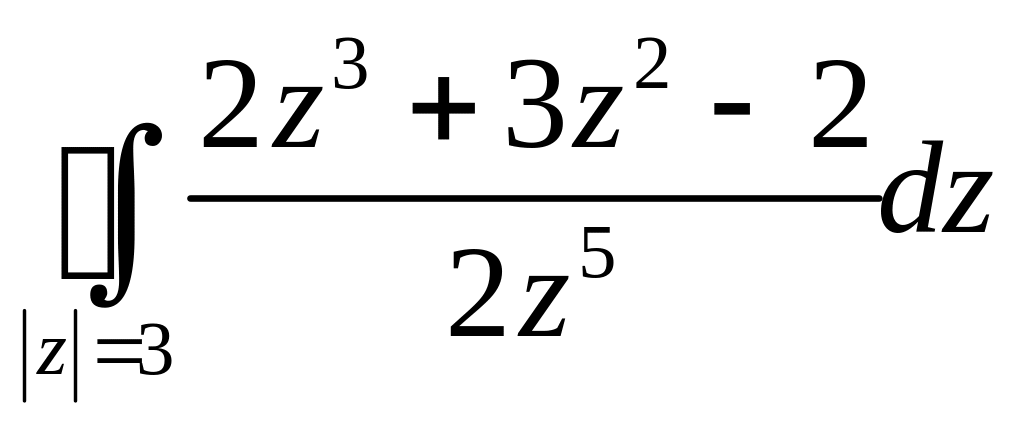 .
.
2.

Решение. 1. Внутри
контура
![]() имеет полюс 5-го порядка в точке
.
имеет полюс 5-го порядка в точке
.
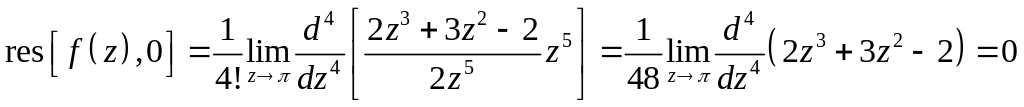
Тогда
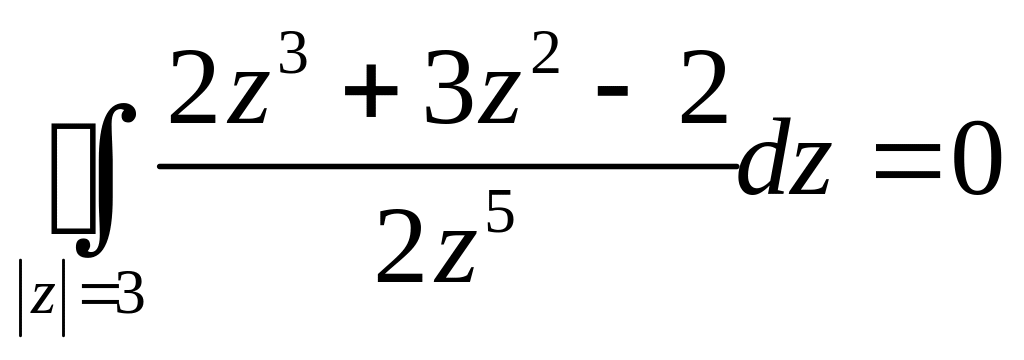 .
.
2. Внутри контура
![]() имеет существенно особую точку
.
имеет существенно особую точку
.
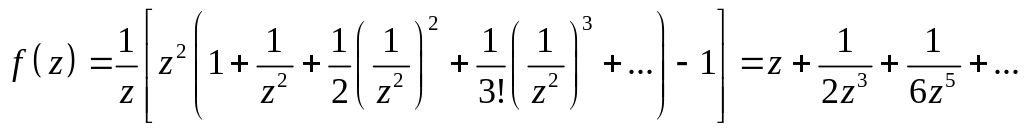
т.е. ряд Лорана имеет бесконечное число членов в главной части разложения.
Из разложения
следует
![]()
Тогда
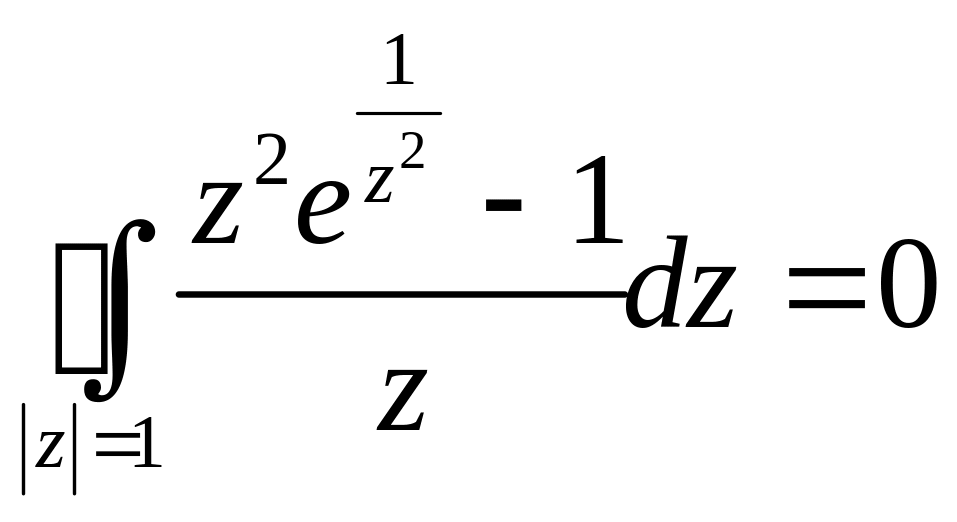
Задача 2.15. Вычислить интегралы:
1.
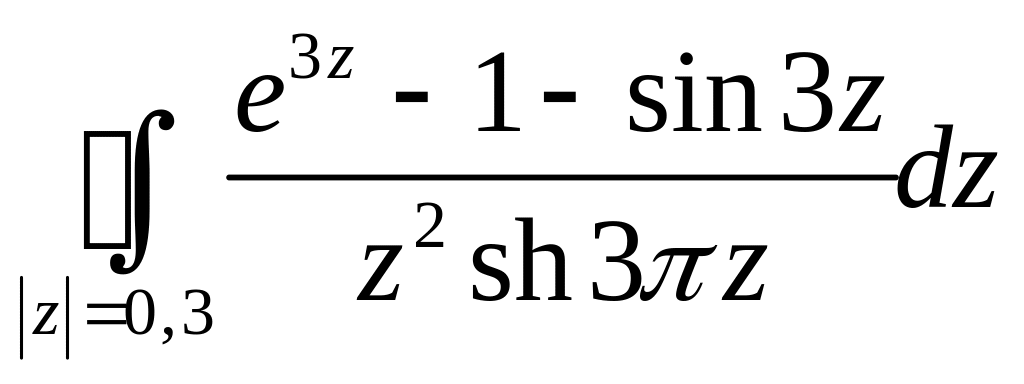 .
.
2.

Решение. 1. Внутри
контура
![]() имеет полюс 1-го порядка в точке
.
имеет полюс 1-го порядка в точке
.


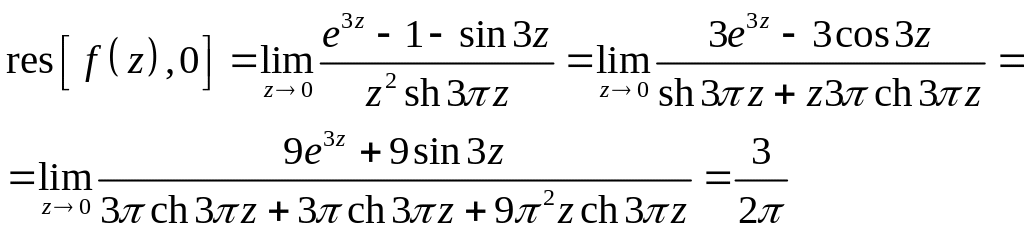
Тогда
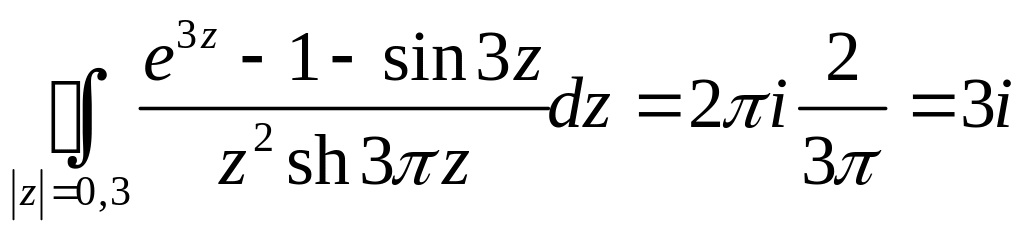
2. Внутри контура
![]() имеет полюс 1-го порядка в точке
,
т. к.
имеет полюс 1-го порядка в точке
,
т. к.
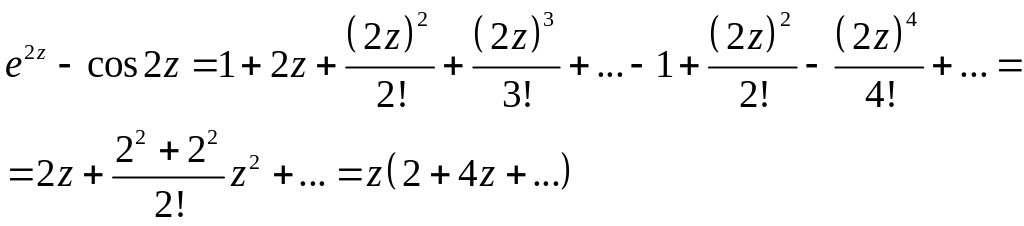
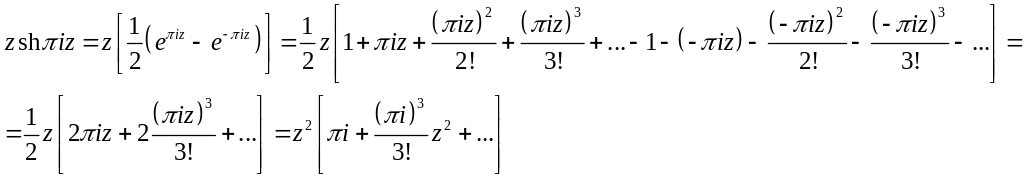
![]()
Тогда
 .
.
Задача 2.16. Вычислить интегралы:
1.
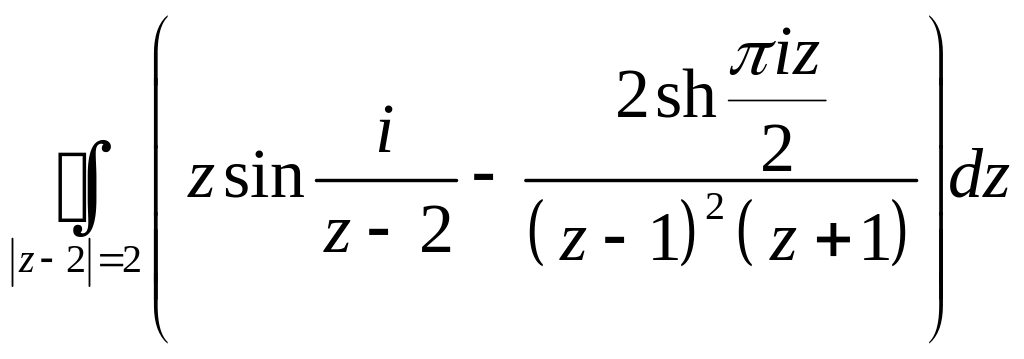 .
.
2.
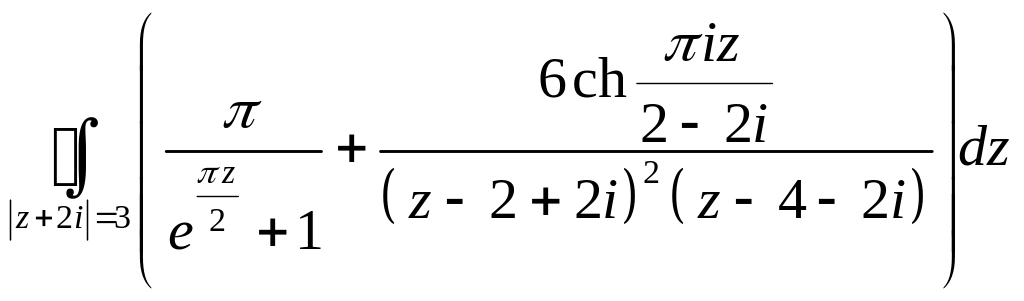
Решение. 1. Внутри
контура
![]() функция
функция
![]() имеет существенно особую точку
имеет существенно особую точку
![]() ,т.
к.
,т.
к.
![]() не существует, функция
не существует, функция
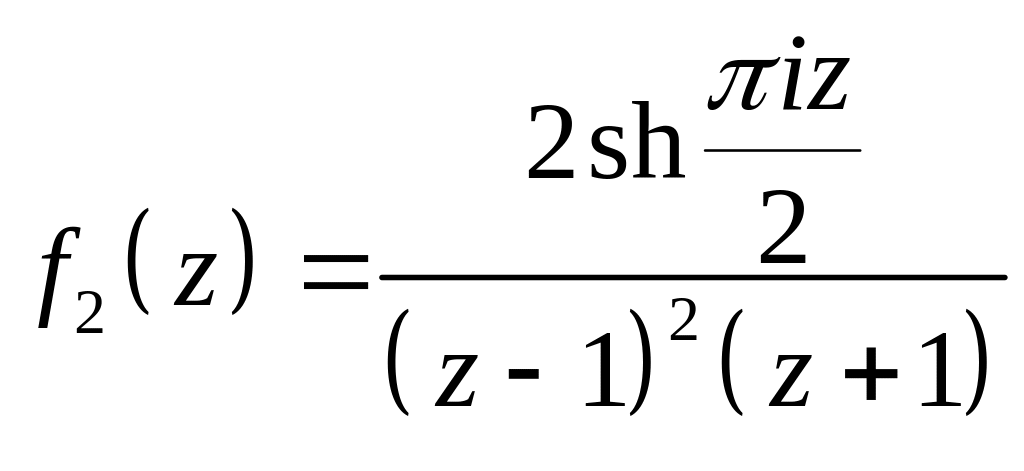 имеет полюс 2-го порядка в точке
.
имеет полюс 2-го порядка в точке
.
Найдем вычеты функций в этих точках:
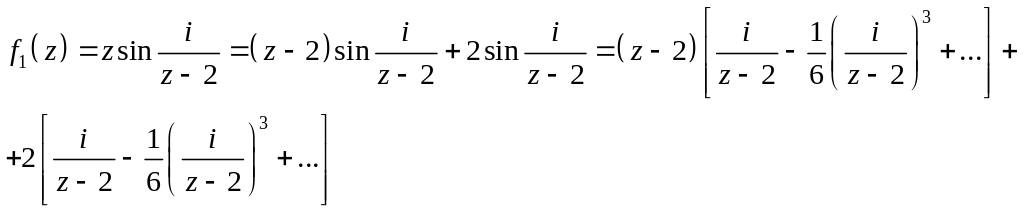
![]()
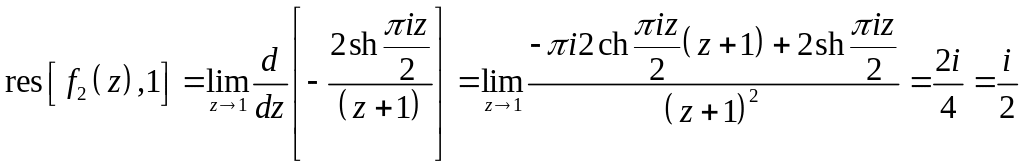
Тогда
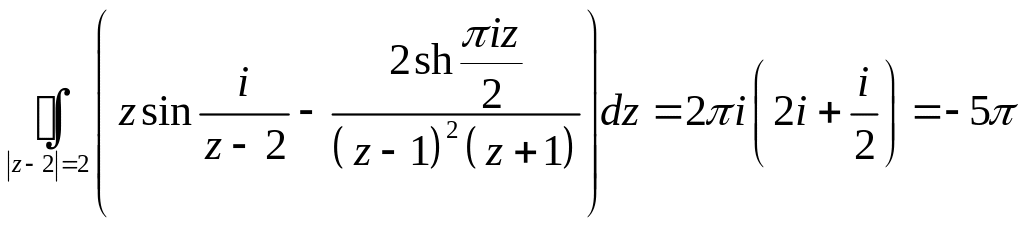 .
.
2. Внутри контура
функция
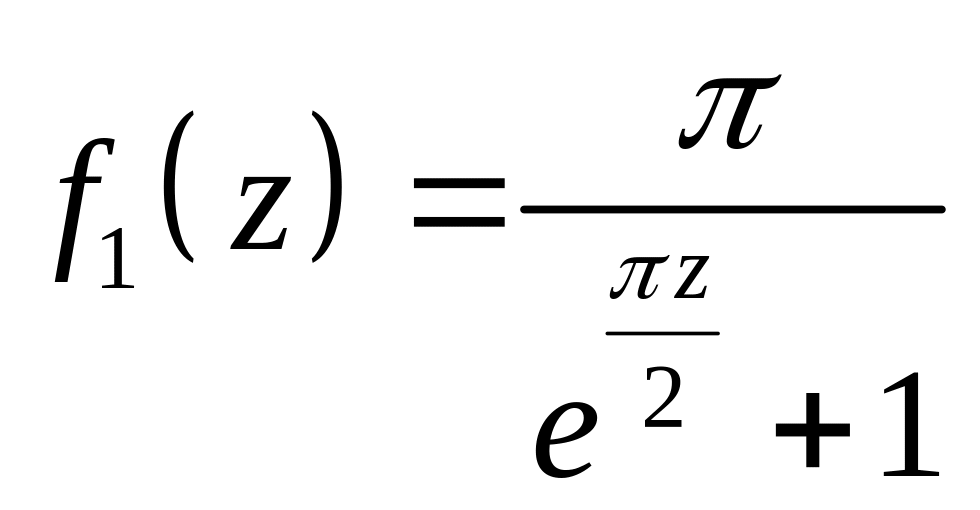 имеет полюс 1-го порядка в точке
имеет полюс 1-го порядка в точке
![]() ,
т.к.
,
т.к.
![]() при
при
![]() .
.
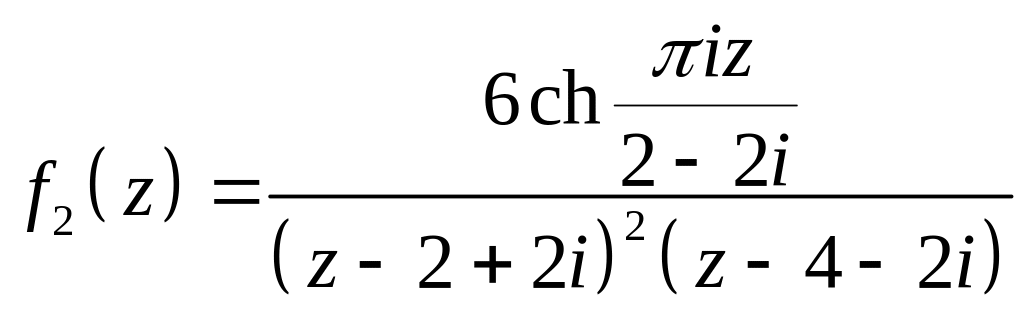 имеет полюс 2-го
порядка в точке
имеет полюс 2-го
порядка в точке
![]() .
.
Найдем вычеты функций в этих точках:
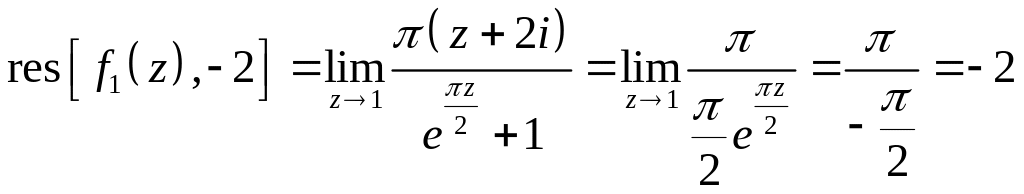
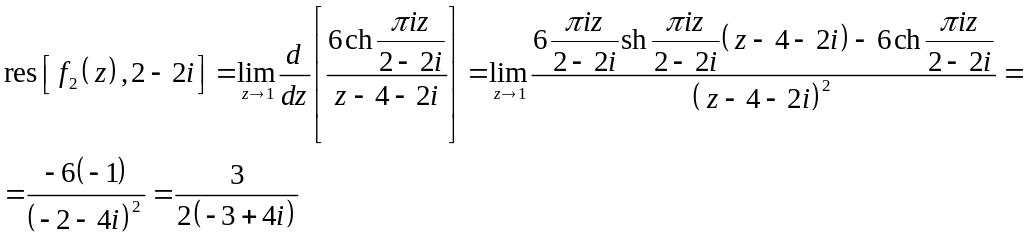
Тогда
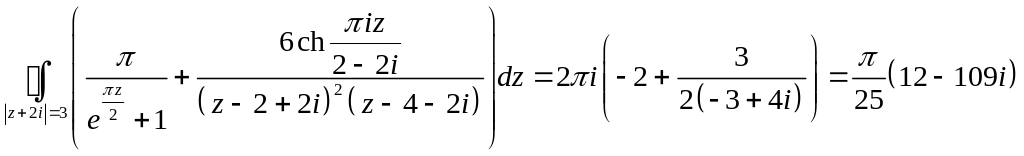
Задача 2.17. Вычислить интегралы:
1.
![]()
2.
![]()
Решение. 1. Рассмотрим интеграл вида
![]()
Пусть
,
тогда
![]()
При изменении
от
![]() до
переменная
пробегает окружность
в положительном направлении, и исходный
интеграл сведется к интегралу по
замкнутому контуру
,
т.е.
до
переменная
пробегает окружность
в положительном направлении, и исходный
интеграл сведется к интегралу по
замкнутому контуру
,
т.е.
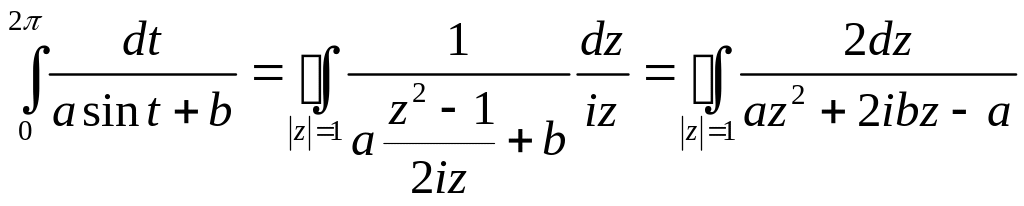
Корни уравнения
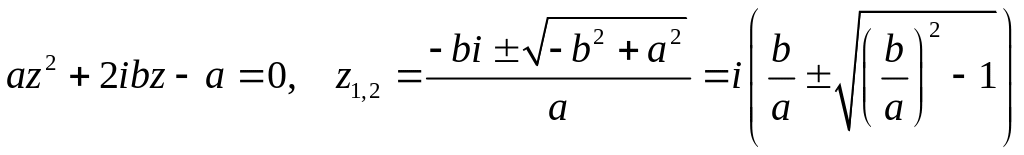
Внутри контура
лежит лишь одна точка
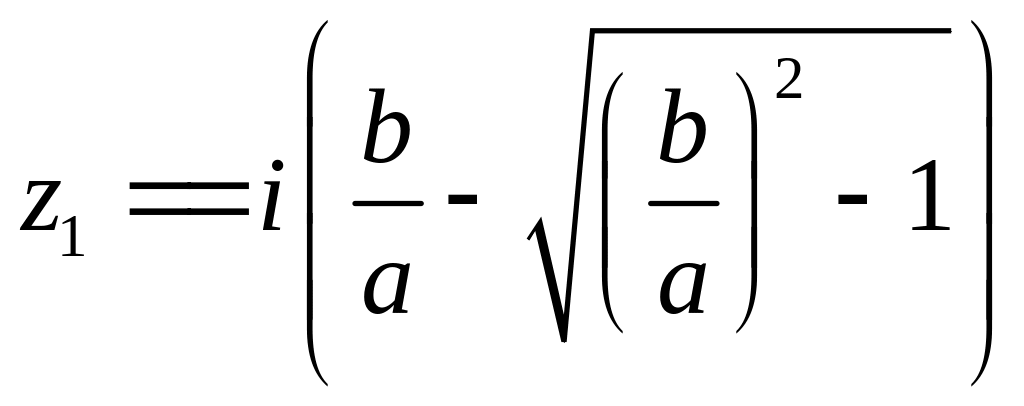 являющаяся полюсом 1-го порядка
являющаяся полюсом 1-го порядка
![]()
Тогда
![]()
Применяя полученный результат к конкретным интегралам, будем иметь:
1.
![]()
2.
![]()
Задача 2.18. Вычислить интегралы:
1.
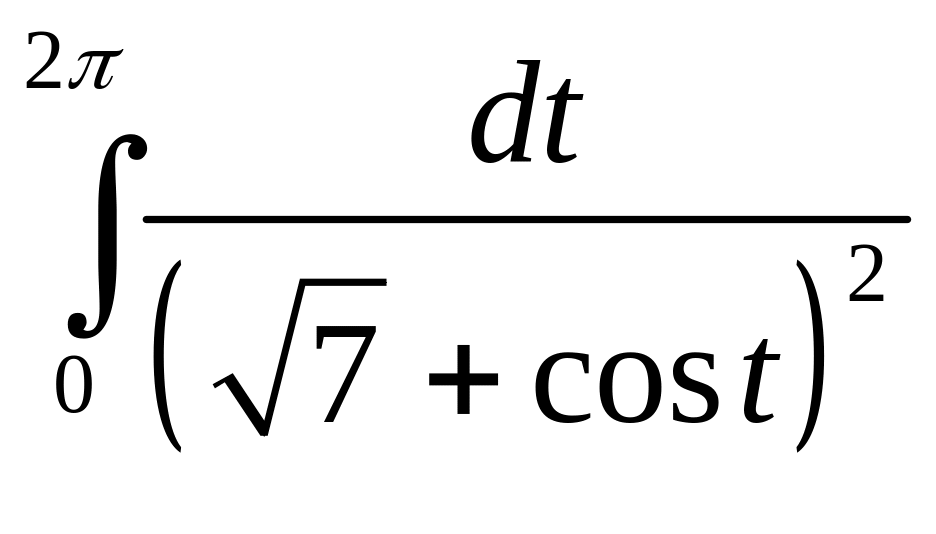
2.
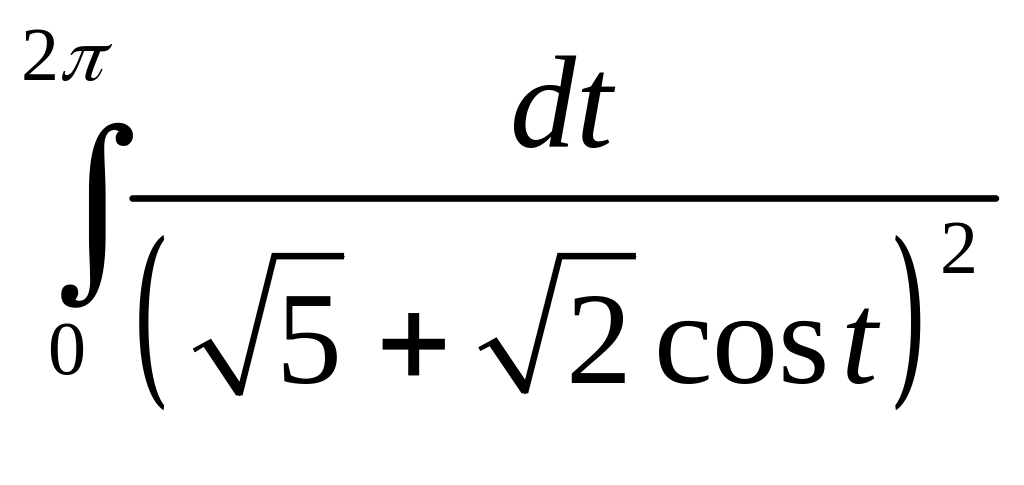
Решение. Рассмотрим интеграл вида
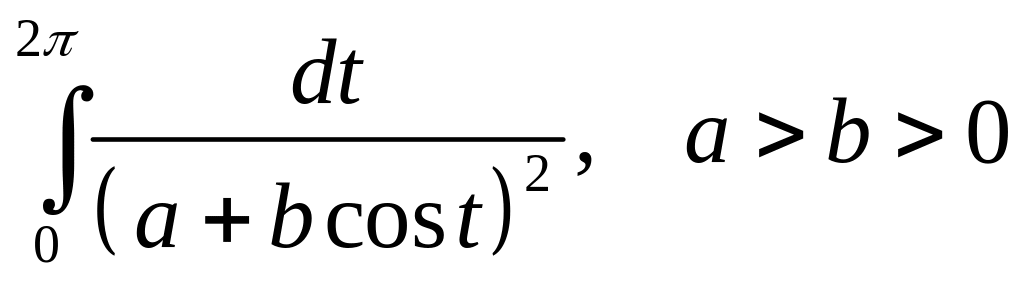
Пусть
,
тогда
![]()
При изменении от до переменная пробегает окружность в положительном направлении, и исходный интеграл сведется к интегралу по замкнутому контуру , т.е.
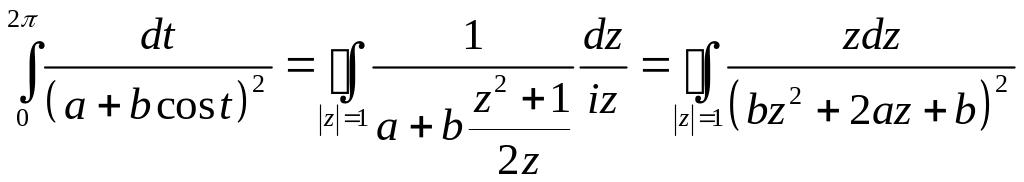
Корни уравнения
![]() ,
,
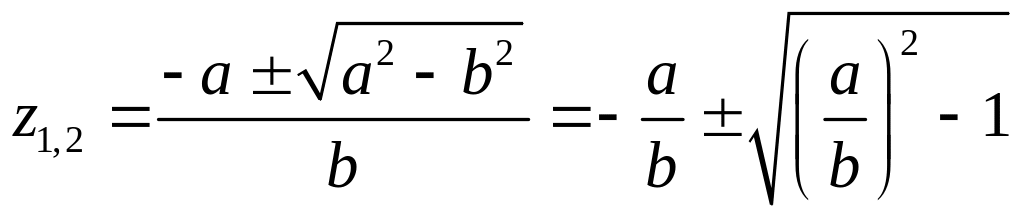
Внутри контура
лежит лишь одна точка
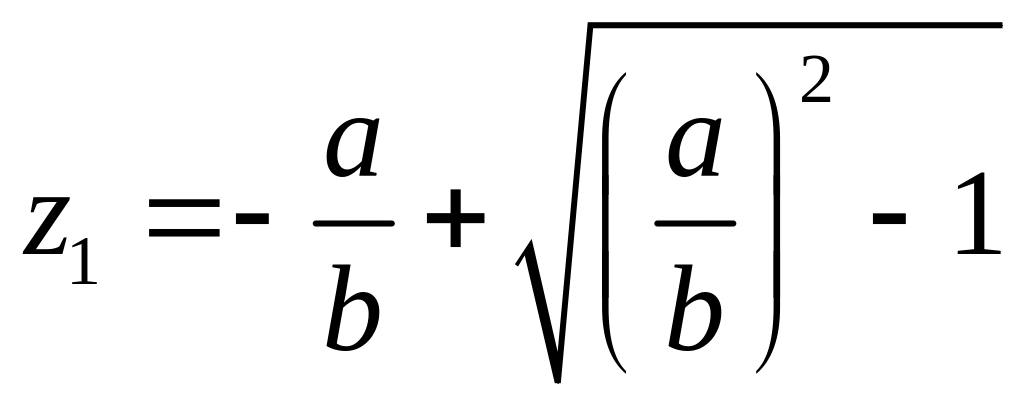 ,
являющаяся полюсом 2-го порядка
,
являющаяся полюсом 2-го порядка
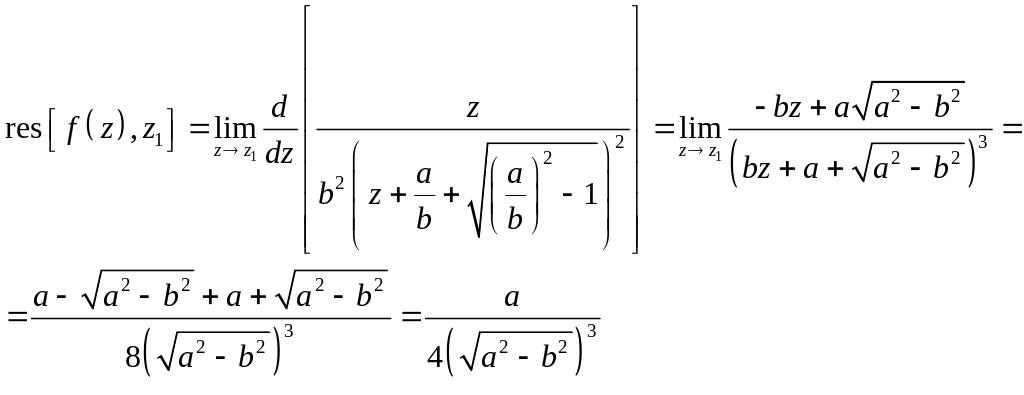
Тогда

Применяя полученный результат к нашей задаче, будем иметь
1.
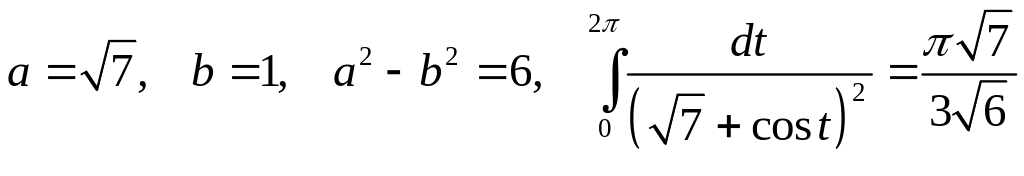
2.

Задача 2.19. Вычислить интегралы:
1.
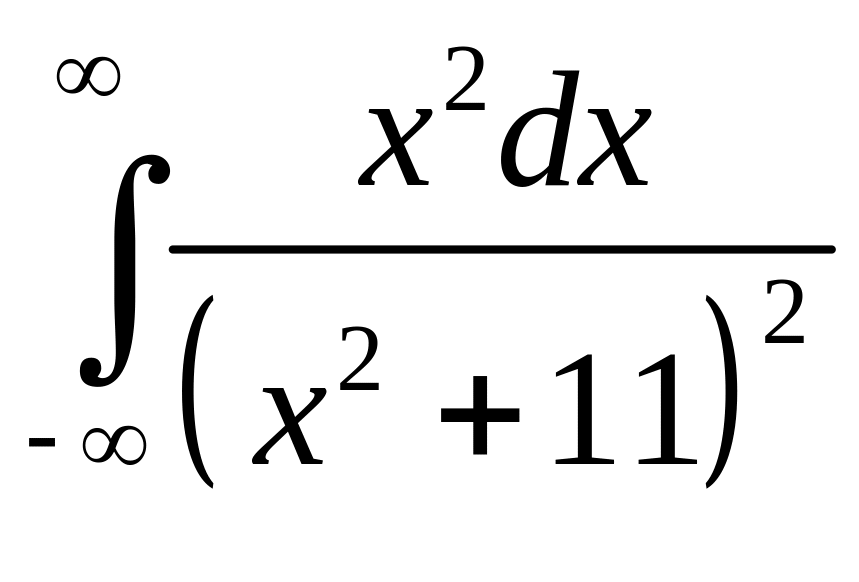
2.
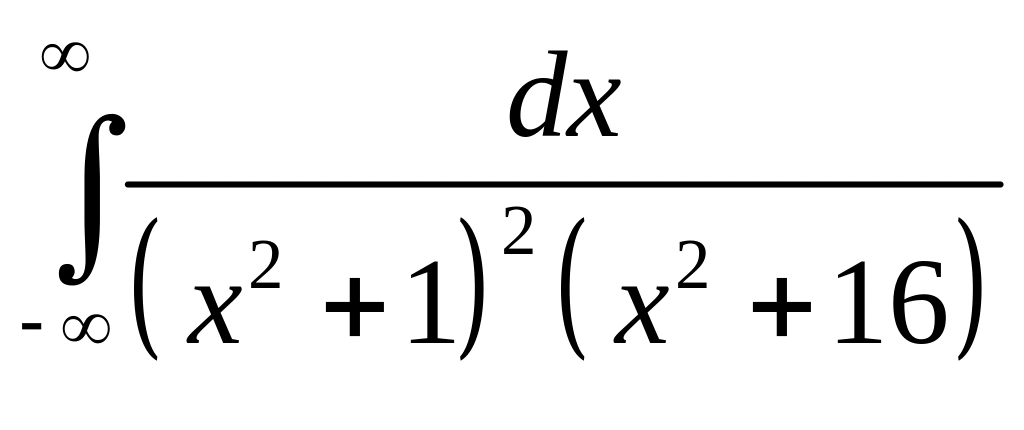
Решение. 1.
Функция
 совпадает с функцией
совпадает с функцией
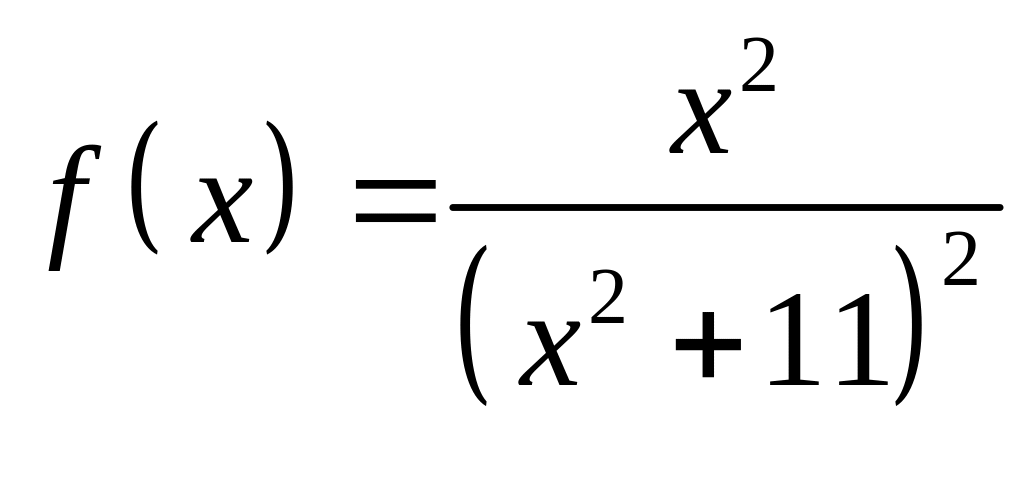 на оси ОХ и имеет в верхней полуплоскости
полюс 2-го порядка в точке
на оси ОХ и имеет в верхней полуплоскости
полюс 2-го порядка в точке
![]() .
.

Тогда
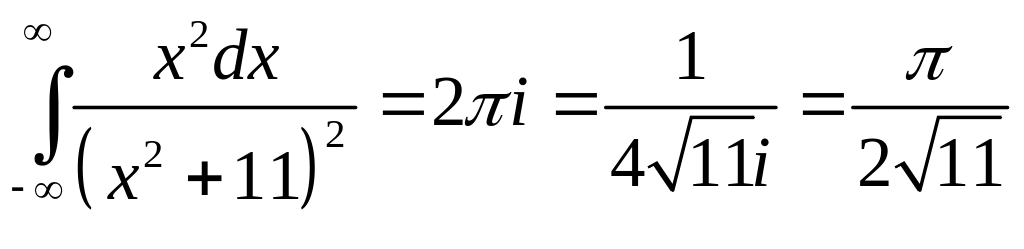 .
.
2. Функция
 совпадает с функцией
совпадает с функцией
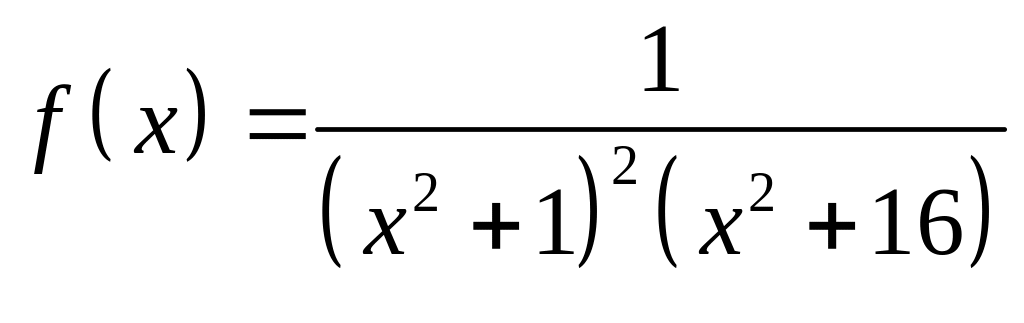 на оси ОХ и имеет в верхней полуплоскости
две особые точки: полюс 2-го порядка в
точке
на оси ОХ и имеет в верхней полуплоскости
две особые точки: полюс 2-го порядка в
точке
![]() и полюс 1-го порядка в точке
и полюс 1-го порядка в точке
![]() .
.
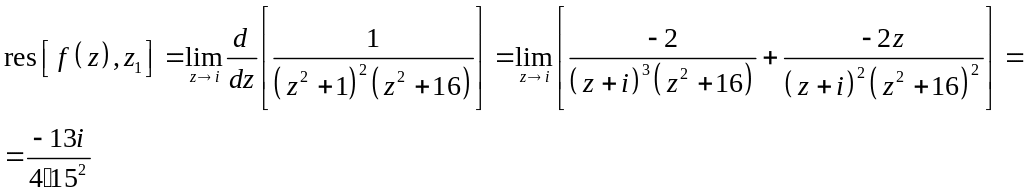
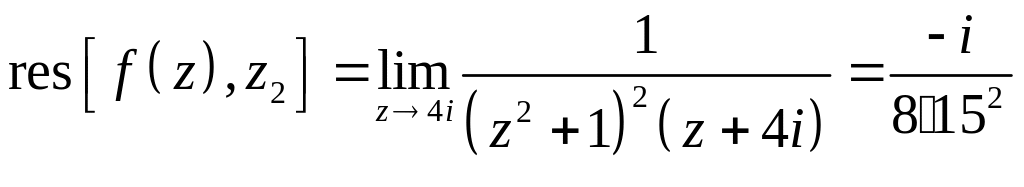
Тогда
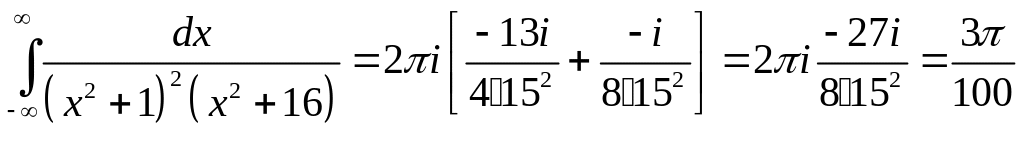 .
.
Задача 2.20. Вычислить интегралы:
1.
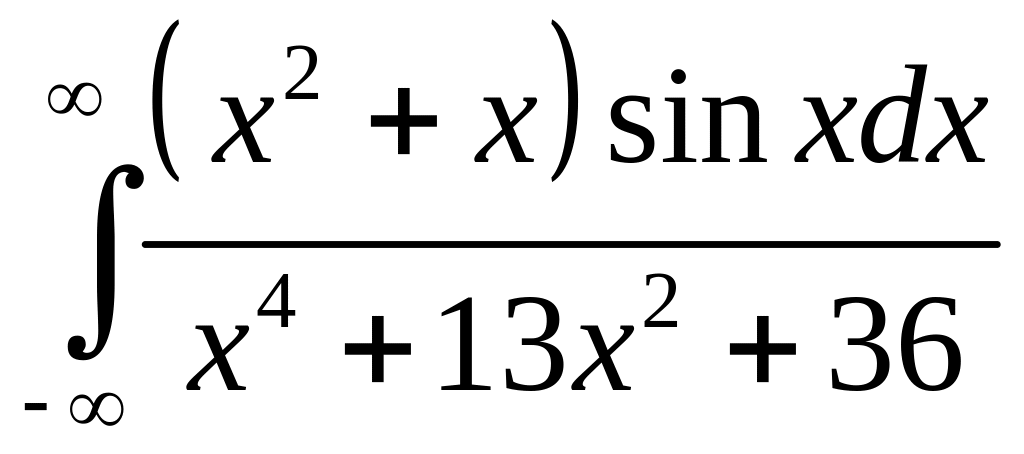
2.
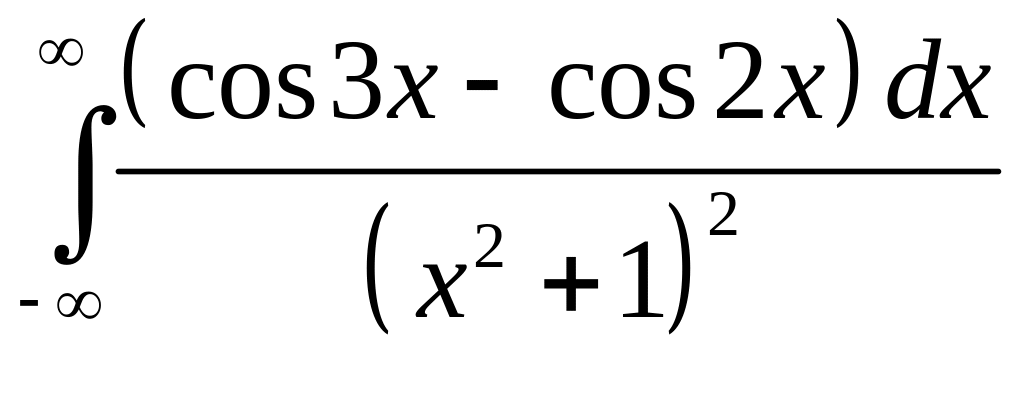
Решение. 1. Рассмотрим
функцию
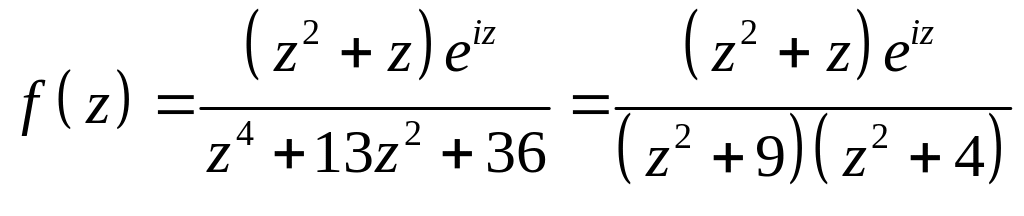 ,
которая имеет в верхней полуплоскости
в точках
,
которая имеет в верхней полуплоскости
в точках
![]() и
и
![]() полюсы 1-го порядка.
полюсы 1-го порядка.
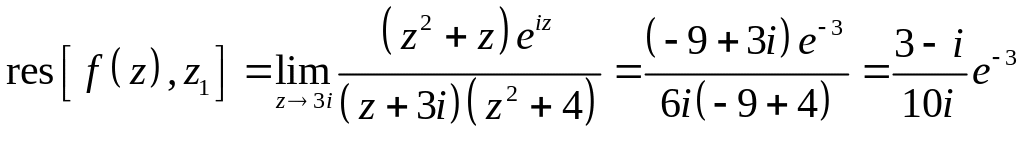

Тогда
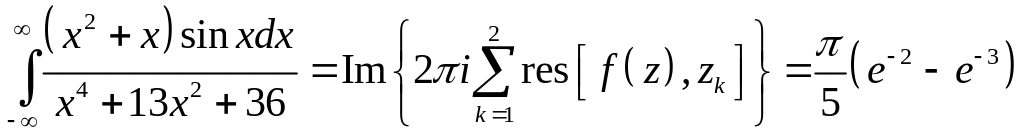 .
.
2. Рассмотрим
функцию
 ,
которая имеет в верхней полуплоскости
полюс 2-го порядка в точке
.
,
которая имеет в верхней полуплоскости
полюс 2-го порядка в точке
.

Тогда
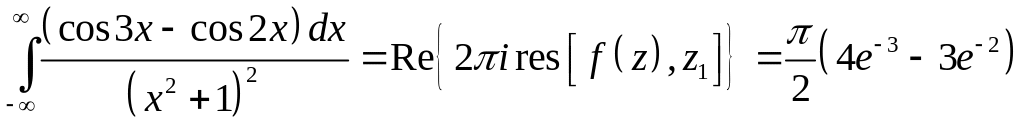 .
.
Задача 2.21. Выяснить, во что преобразуется геометрическая фигура при отображении с помощью функции .
1.
![]() ,
полуплоскость
,
полуплоскость
![]()
2.
![]() ,
полоса
,
полоса
![]()
Решение. 1. Дробно-линейное отображение строим по 3-м парам точек и направлению обхода.
Например,
![]() - точка на единичной окружности;
- точка на единичной окружности;
![]() - точка на единичной
окружности
- точка на единичной
окружности
![]() - точка на единичной
окружности.
- точка на единичной
окружности.
Таким образом, полуплоскость преобразуется во внешнюю область единичного круга (см. рис 2.7)
2.
![]()
Рассматриваемое отображение можно рассматривать как последовательные отображения:
![]() – поворот на угол
– поворот на угол
![]() и расширение полосы вдвое;
и расширение полосы вдвое;
![]() – полученная
полоса отображается на полуплоскость
– полученная
полоса отображается на полуплоскость
![]() ;
;
![]() – дробно-линейная
функция отображает полуплоскость на
внутренность единичного круга. (см.
рис 2.8)
– дробно-линейная
функция отображает полуплоскость на
внутренность единичного круга. (см.
рис 2.8)
Задача 2.22. Найти круг сходимости степенного ряда и определить сходимость ряда на границе круга.
1.
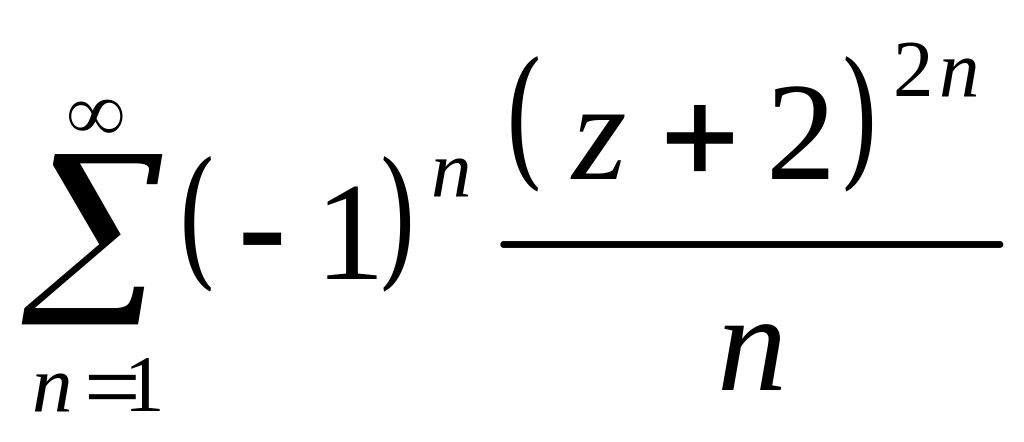 ;
2.
;
2.
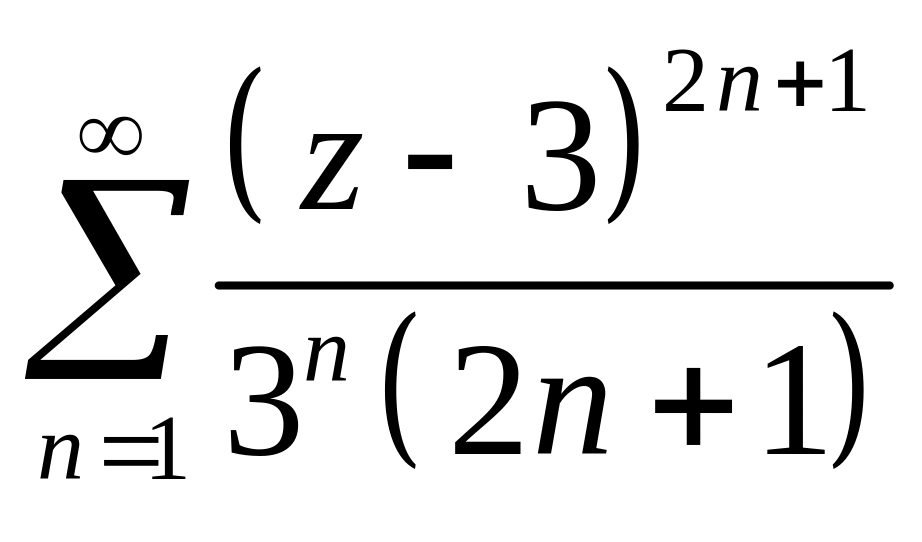 .
.
Решение
1. Запишем
–й
и
![]() –й
члены ряда:
–й
члены ряда:
![]() ,
,
![]()
По
признаку Даламбера
![]() .
В нашем случае:
.
В нашем случае:

Отсюда,
ряд сходится в круге
![]() .
При этом, ряд сходится абсолютно, если
и равномерно, если
.
При этом, ряд сходится абсолютно, если
и равномерно, если
![]() .
.
На
границе круга
![]() имеем числовой ряд с действительными
членами
имеем числовой ряд с действительными
членами
![]() ,
который по признаку Лейбница сходится
условно.
,
который по признаку Лейбница сходится
условно.
2. Запишем –й и –й члены ряда:
 ,
,
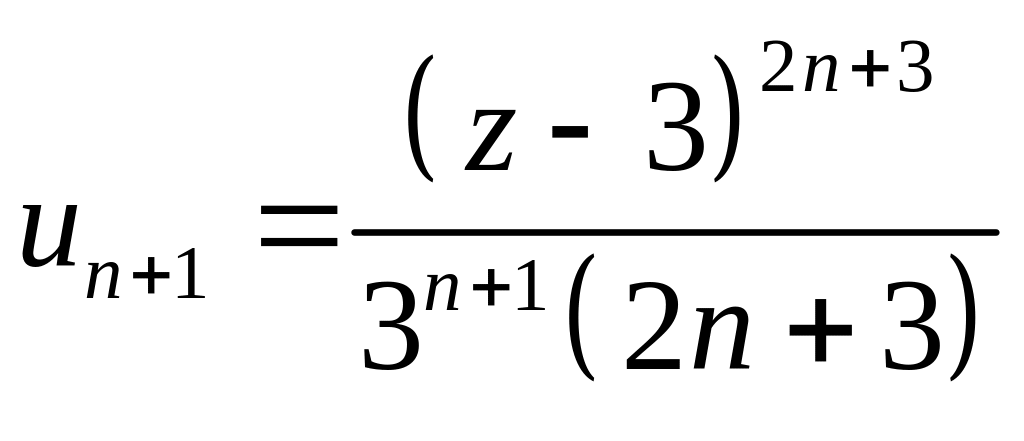
По признаку Даламбера
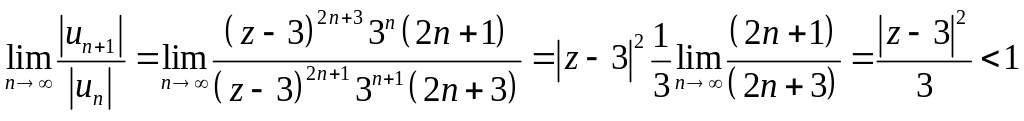 .
.
Отсюда,
ряд сходится в круге
![]() . При этом, ряд сходится абсолютно, если
и равномерно, если
. При этом, ряд сходится абсолютно, если
и равномерно, если
![]() .
.
На
границе круга
![]() имеем числовой ряд с действительными
членами
имеем числовой ряд с действительными
членами
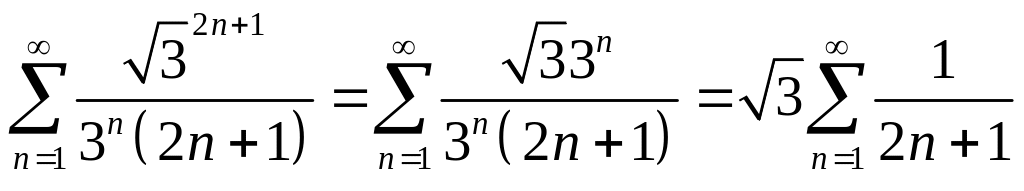 .
.
Ряд
![]() сравним с гармоническим рядом
сравним с гармоническим рядом
![]() .
.
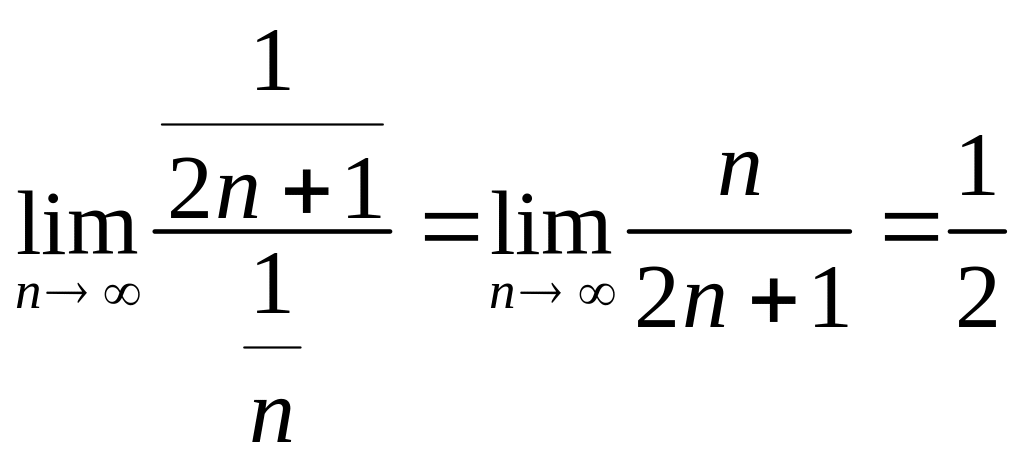
Ряд расходится, следовательно по признаку сравнения ряд тоже расходится. Следовательно, исходных ряд на границе круга расходится.
