1.9Вычеты

Пусть - изолированная особая точка функции , Вычетом функции относительно точки называется коэффициент ряда Лорана для функции в окрестности точки . Для вычета функции относительно точки приняты обозначения или Вычет функции относительно точки определяется по формуле:

где – замкнутый кусочно-гладкий контур, целиком лежащий в области аналитичности функции и не содержащий внутри других особых точек функции , кроме точки .

Если - устранимая особая точка функции , то

Если - полюс порядка функции , то

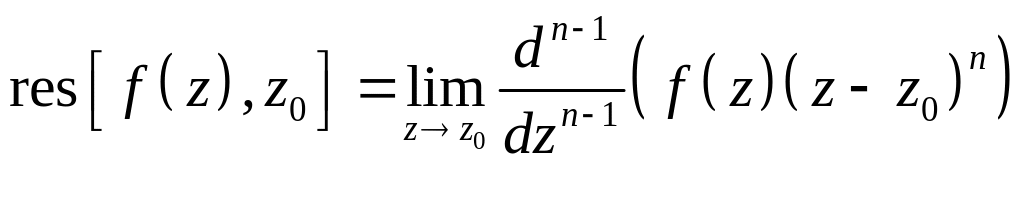
Если - полюс 1-го порядка функции , то

Если , где - аналитические функции в окрестности точки и , , т.е. точка есть полюс первого порядка функции , то

Если - существенно особая точка функции , то

Где – любой кусочно-гладкий замкнутый контур, целиком принадлежащий области аналитичности функции и не содержащий внутри себя других особых точек, кроме точки .

Имеет место теорема (основная теорема о вычетах). Если функция является аналитической в области за исключением конечного числа изолированных особых точек, то интеграл от этой функции, вычисленный в положительном направлении, по любому замкнутому контуру , целиком лежащему в области и не проходящему через особые точки, равен произведению числа на сумму вычетов относительно всех особых точек, заключенных внутри контура , т.е.

1.10Вычисление определенных интегралов от функций действительного переменного

Пусть заданная на действительной оси функция может быть продолжена на верхнюю полуплоскость комплексной плоскости так, что аналитическое продолжение является аналитической функцией в области всюду за исключением конечного числа изолированных особых точек, причем

Тогда

Пусть может быть продолжена на верхнюю полуплоскость комплексной плоскости так, что не имеет особых точек на оси , является аналитической в верхней полуплоскости всюду за исключением конечного числа изолированных особых точек и равномерно относительно стремится к нулю при

Тогда для

Отсюда

Пусть - рациональная функция , непрерывная внутри промежутка интегрирования.

Полагая , получим

Тогда

,

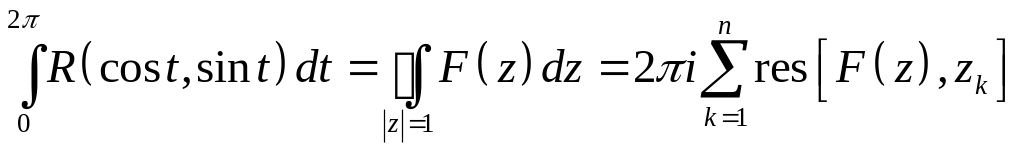где вычеты функции вычисляются относительно всех особых точек, принадлежащих области .

1.11Конформные отображения

Геометрически заданную на области функцию можно рассматривать как отображение области плоскости на некоторое множество плоскости , являющееся совокупностью значений , соответствующих всем . Взаимно однозначное отображение области плоскости на область плоскости называется конформным, если в каждой точке области оно обладает свойствами сохранения углов и постоянства растяжения. Для того, чтобы отображение области , задаваемое функцией , было конформным, необходимо и достаточно, чтобы была однолистной и аналитической в области функцией , при этом всюду в области .

Например, отображение, осуществляемое линейной функцией можно представить в виде композиции гомотетии, поворота и параллельного переноса плоскости. При этом любая окружность отображается на окружность, любая прямая – на прямую, любой открытый круг – на открытый круг, любая открытая полуплоскость – на открытую плоскость. Отображение может быть получено по двум парам точек и .

Отображение, осуществляемое дробно-рациональной функцией можно представить в виде композиции параллельного переноса, инверсии, осевой симметрии, гомотетии и поворота плоскости. При этом любая окружность, не проходящая через точку , отображается на окружность; окружность, проходящая через точку - на прямую; любая прямая, не проходящая через точку - на окружность; прямая, проходящая через точку – на прямую; любой открытый круг, для которого точка - является внешней – на открытый круг; открытый круг, для которого точка - является граничной – на открытую полуплоскость (и обратно). Дробно-рациональное отображение может быть получено по трем парам точек , и .

Функция однолистна в любой полосе шириной менее , параллельной действительной оси. Она отображает полосу на всю плоскость с разрезом по действительной отрицательной полуоси. Вся плоскость отображается на бесконечнолистную риманову поверхность.

Обратная функция однозначна на этой римановой поверхности, а ее главное значение определяет отображение всей плоскости с разрезом на полосу .