57

Московский государственный технический университет

им. Н.Э. Баумана

А.В. Абрагин, Дубровин В.М.

Теория функций комплексного переменного

Методические указания к выполнению домашнего задания

Под редакцией

Москва

Издательство МГТУ им.Н.Э. Баумана

2005

В данном пособии изложены основы теории функций комплексного переменного. Приведены основные формулы, необходимые для выполнения типового расчета. Дано решение типовых задач.

В пособии представлены варианты задач типового расчета по курсу «Теория функций комплексного переменного»

Методические указания предназначены для студентов, изучающих курс «Теория функций комплексного переменного»

1Основные теоретические положения и расчетные формулы.

1.1Извлечение корня n-ой степени из комплексного числа:

Корень -ой степени из комплексного числа имеет различных значений, которые находятся по формуле:

1.2Элементарные функции комплексного переменного:

Значения показательной функции комплексного переменного вычисляются по формуле:

Показательная функция обладает свойствами:

, , т.е. является периодической функцией с основным периодом .

Тригонометрические функции и выражаются через показательную функцию следующим образом:

,

Функции и - периодические с действительным периодом и имеют только действительные нули и соответственно.

Функции и определяются соотношениями:

,

Для тригонометрических функций комплексного переменного остаются в силе все известные формулы тригонометрии.

Гиперболические функции определяются соотношениями:

При этом справедливы соотношения, связывающие гиперболические и тригонометрические функции

Логарифмическая функция определяется как функция обратная показательной:

Значение функции, которое получается при , называется главным значением и обозначается

Логарифмическая функция обладает свойствами

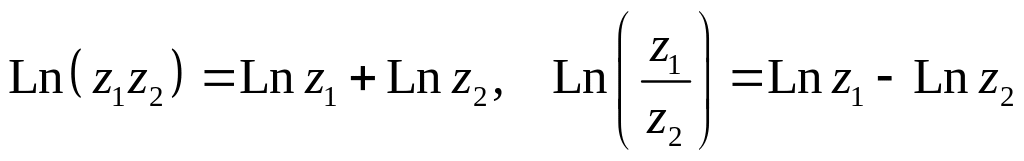
Функции определяются как обратные к функциям соответственно. Так, если , то называется арккосинусом числа и обозначается . Все эти функции являются многозначными и выражаются через логарифмическую:

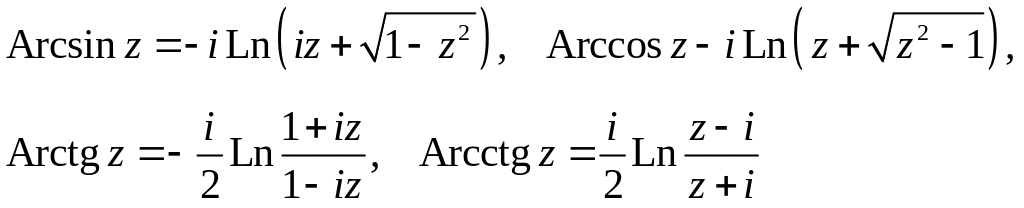
Значения, соответствующие главному значению логарифма, обозначаются соответственно и называются главными значениями этих функций.

Степенная функция , где - любое комплексное число, определяется соотношением:

Эта функция многозначная, значение называется главным значением.

Показательная функция определяется равенством:

Главное значение этой функции .

1.3Кривые на комплексной плоскости.

Уравнение вида

определяет на комплексной плоскости кривую, параметрические уравнения которой имеют вид:

Исключив параметр из этих уравнений (если это возможно), получим уравнение кривой вида .

1.4Дифференцирование функций комплексного переменного

Пусть функция определена в некоторой области комплексного переменного . Пусть и принадлежат области .

Если , то:

Обозначим и соответственно действительную и мнимую часть функции , т.е.

Тогда в каждой точке, в которой существует , выполняются соотношения:

,

называемые условиями Коши-Римана.. Верно и обратное, если в некоторой точке выполняются условия Коши-Римана, а функции и дифференцируемы, то функция является дифференцируемой в точке как функция комплексного переменного .

Функция называется аналитической в точке , если она дифференцируема в этой точке и некоторой ее окрестности. Если является аналитической в каждой точке области , она называется аналитической в области .

Производная аналитической функции определяется по формулам:

Пользуясь условиями Коши-Римана можно восстановить аналитическую функцию , если известна ее действительная часть или мнимая часть .

Пусть, например, . Найти аналитическую функцию .

Из условий Коши-Римана имеем

Интегрируя последнее уравнение по , получим

Отсюда

Таким образом,

и

Постоянная может быть определена, если задано начальное условие .