Задания:

1. Рассмотреть случаи линейной круговой и эллиптической поляризаций для прозрачной и поглощающей сред.

2. Рассмотреть различные виды поляризации в 3-х мерном пространстве.

Практическая работа №5 Исследование волновых явлений на границе раздела двух диэлектриков

Рассмотрим отражение, и преломление монохроматической плоской электромагнитной волны на плоской границе раздела между однородными средами. Падение происходит из прозрачной среды; для второй же среды предположения о прозрачности делать не будем. Будем отмечать величины, относящиеся к падающей и отраженной волнам, соответственно индексами 0 и 1,а к преломленной волне – индексом 2 (см. рис. 5.1).

На границе раздела двух диэлектриков выполняются условия при отсутствии зарядов и токов:

D n(2) = Dn(1); Bn(2) = Bn(1);

Eτ(2) = Eτ(1); Hτ (2) = Hτ(1). (5.1)

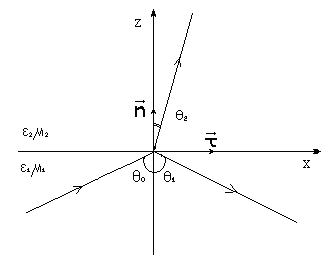
Рисунок 5.1

Напряженности электрического поля падающей, отраженной и преломленной плоских волн выражаются формулами:

E₀ = E₀(0)exp{i((k₀, r) – ₀t)};

E₁ = E₀(1)exp{i((k₁, r) – ₁t)};

E₂ = E₀(2)exp{i((k₂, r) – ₂t)}. (5.2)

Волновое число

где λ —  длина волны; ν (греческая буква «ню») — частота; v_p = v_ф — фазовая скорость волны; ω — угловая частота; E — энергия; ħ — редуцированная постоянная Планка (постоянная Дирака); c — скорость света в вакууме.

Граничное условие для тангенциальных составляющих напряженности электрического поля имеет вид

[E0(0)exp{i((k0,r)-0t)}+E0(1)exp{i((k1,r)-1t)}]τ =

=[E0(2)exp{i((k2,r)-2t)}]τ , (5.3)

причем начало отсчета радиус-вектора произвольно. Выберем начало отсчета радиус-вектора, как показано на рисунке, в плоскости раздела двух сред.

Из (5.3) следует выполнение двух равенств

0 = 1 = 2 ,

(k0,r)=(k1,r)=(k2,r)

для огромного интервала частот.

Положим r = τ.

k_0x=k_1x = k_2x,

тогда

(/c)n₁sinΘ₀=(/c)n₁sinΘ₁ = (/c)n₂sinΘ₂ ,

откуда следует равенство углов падения и отражения:

Θ₀=Θ₁

и закон преломления.

(sinΘ₀)/(sinΘ₂)=n₂/n₁=n₁₂

Соотношения между амплитудами падающей, отраженной и преломленной волнами в общем случае (формулы Френеля).

1. Электрическое поле E0 перпендикулярно к плоскости падения:

2. Электрическое поле E0 лежит в плоскости падения:

Пример 5.1

Соотношение амплитуд падающей и отраженной волн для случая n₁ < n₂ в зависимости от различного угла падения (Электрическое поле E0 лежит в плоскости падения)

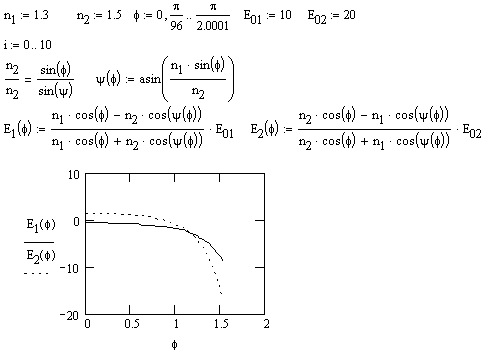
Задания:

1. Рассмотреть соотношение амплитуд падающей и отраженной волн для случая n₁ > n₂ в зависимости от различного угла падения (Электрическое поле E0 лежит в плоскости падения).

2. Рассмотреть соотношение амплитуд падающей и отраженной волн для случая n₁ > n₂ в зависимости от различного угла падения (Электрическое поле E0 перпендикулярно плоскости падения).

3. Рассмотреть соотношение амплитуд падающей и отраженной волн для случая n₁ < n₂ в зависимости от различного угла падения (Электрическое поле E0 перпендикулярно плоскости падения).