3. Дизъюнктивные и конъюнктивные нормальные формы. Полиномы жегалкина Основные понятия

Формула (формула), гдедля всех— называетсяконъюнкцией(дизъюнкцией) над множеством переменных.

Конъюнкция (дизъюнкция) называется элементарной(э.к., э.д.), еслиприjk. Выражения видабудут называтьсябуквами (литера-лами). Число символов (букв) в э.к. (э.д.) называетсярангомэ.к. (э.д.).

Формула вида D=, где– элементарные конъюнкции, называется дизъюнктивной нормальной формой(д.н.ф.).

Формула вида K=, где– дизъюнкции, называетсяконъюнктивной нормальной формой(к.н.ф.). Числоsназываетсядлинойд.н.ф. (к.н.ф.).

Д.н.ф. называется совершенной, если она составлена из попарно различных элементарных конъюнкций рангаn.

Элементарная конъюнкция называется монотонной, если она не содержит отрицаний переменных.

Формула , где– попарно различные монотонные элементарные конъюнкции, а, называетсяполиномом Жегалкинаилиполиномом по модулю 2. Наибольший из рангов э.к., входящих в полином, называетсястепеньюэтого полинома, числоsназывается длиной полинома.

ЗАДАЧИ

3.1. С помощью эквивалентных преобразований привести к д.н.ф. формулу:

3.2. Представить в виде совершенной д.н.ф. следующие функции:

3.3. С помощью преобразований видаперейти от заданной д.н.ф. к совершенной:

3.4. Подсчитать число функций, для которых совершенная к.н.ф. является одновременно и д.н.ф.

3.5. Представить в виде совершенной к.н.ф. функцию

3.6. Показать, что если в совершенной д.н.ф. знакVвсюду заменить на, то получится формула,

эквивалентная исходной.

3.7. Доказать, что для любой ф.а.л. существует единственное разложение в полином Жегалкина.

3.8. Является ли линейной функция

3.9. Представить в виде полинома Жегалкина ф.а.л. :

3.10. Показать, что функция, реализуемая многочленом степениk>0, обращается в 1 не менее чем навекторах

из .

3.11. Разложить по переменной, применяя формулы

,

и представить в совершенной к.н.ф. и совершенной д.н.ф. функции:

3.12. Представить в совершенной к.н.ф.компоненты функции,

рассматривая их как функции, зависящие только от «оставшихся» переменных.

3.13. Доказать, что еслидля, то.

3.14. Найти длину совершенной д.н.ф. функции:

3.15. Показать, чтоxявляется существенной переменной функцииfтогда и только тогда, когдаxявно входит

в полином Жегалкина функции f.

4. Минимизация булевых функций Основные понятия

Допустимой конъюнкциейилиимпликантомфункцииназывается элементарная конъюнкцияКнад множеством переменных, такая, что. ИмпликантКфункцииназываетсяпростым импликантом, если после отбрасывания любой буквы изКполучается э.к., не являющаяся импликантом функции.

Дизъюнкция всех простых импликантов функции называетсясокращеннойд.н.ф. функции. Д.н.ф. называется:минимальной, если она имеет наименьшее число букв среди эквивалентных ей д.н.ф.;кратчайшей,если она имеет наименьшую длину среди эквивалентных ей д.н.ф.;тупиковой, если отбрасывание любого слагаемого или буквы приводит к неэквивалентной д.н.ф. Если э.к.Kявляется импликантом функции, то множество=образует грань, содержащуюся в множестве= =. Эта грань является интервалом функции, соответствующим импликантуK. Интервал функции, не содержащийся ни в каком другом интервале, называетсямаксимальным интервалом. Максимальные интервалы соответствуют простым импликантам функции.

Метод Блейкаполучения сокращенной д.н.ф. из произвольной д.н.ф. состоит в применении правилобобщенного склеивания=ипоглощения . Правила применяются слева направо. Сперва производятся операции обобщенного склеивания, пока это возможно, на втором — операции поглощения. Для построения сокращенной д.н.ф. можно использовать геометрический или табличный методы (с помощью минимизирующей карты).

ЗАДАЧИ

4.1. С помощью метода Блейка построить сокращенную д.н.ф. функций:

4.2. Построить сокращенную д.н.ф. по заданной к.н.ф.:

4.3. Используя геометрический метод, построить сокращенную д.н.ф. функции:

1) ; 2);

3) .

4.4. С помощью минимизирующей карты построить сокращенную д.н.ф. функции

4.5. Используя метод Блейка, построить сокращенную д.н.ф. функции

4.6. Используя табличный метод минимизации, найти минимальную д.н.ф. функции из задачи 4.5.

4.7. Выяснить, являются ли тупиковыми, кратчайшими или минимальными следующие д.н.ф.:

4.8. Перечислить существенные переменные следующих функций:

4.9. Показать, чтоx₁является фиктивной переменной функцииf(выразив fформулой, в которуюx₁ не входит явно):

4.10. Показать, что x является существенной переменной функцииfтогда и только тогда, когда эта переменная

явно входит в сокращенную д.н.ф. функции f.

4.11. Показать, что переменнаяxявляется существенной переменной функцииf тогда и только тогда, когдаxявно

входит в полином Жегалкина функции f.

4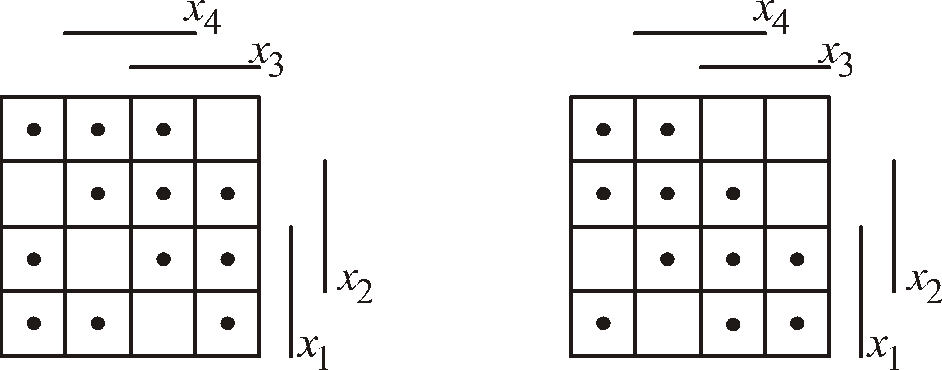.12. Построить сокращенную д.н.ф. для функции, заданной таблицей

а) б)

4.13. Построить все тупиковые д.н.ф. функции