2.5. Обобщенная модель Кельвина — Фойгта.

Сопоставление меха­нических характеристик элемента Кельвина — Фойгта с механи­ческими характеристиками реальных полимеров указывает на существование качественного сходства. Однако попытки количе­ственного описания поведения реальных полимеров при помощи уравнения движения модели Кельвина — Фойгта наталкиваются на такие же затруднения, что и при использовании однокомпонентной модели Максвелла.

В связи с этим была предложена обобщенная модель Кельви­на— Фойгта, характеризуемая спектром податливостей.

Обобщенная модель Кельвина — Фойгта.

Рис. 2.9.

2.6.Модель Алфрея-Гарни (Бургерса-Френкеля)

Модель Алфрея-Гарни

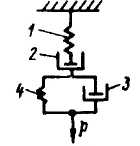
1,4 — пружины; 2, 3 —демпферы.

Рис. 2.10.

Недостатком модели Фойгта-Кельвина является то, что она не описывает компоненты упругой мгновенной деформации и вязкого течения. Этого можно избежать, если воспользоваться обобщенной моделью Алфрея-Гарни (см. рис. 2.10).

При нагружении такой модели деформирование происходит за счет мгновенного растяжения пружины 1 и одновременного вязкого течения в демпфере 2. В результате перемещения поршня демпфера 3 начинает развиваться высокоэластическая деформация, которая прекращается через некоторое время при достижении равновесия в пружине 4. Дальнейшее деформирование модели осуществляется за счет перемещения демпфера 2. Схема развития деформации показана на рис.2 11.

Зависимость развития де­формации во времени для модели Алфрея-Гарни

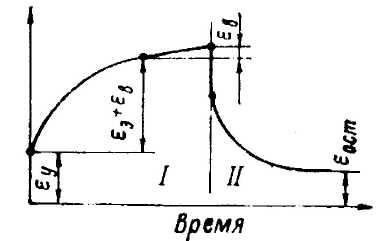
I — нагружение; II — восстанов­ление деформации после снятия нагрузки.

Рис. 2.11.

Таким образом, если нагрузка не меняется во времени, то дефор­мация будет равна накопленной упругой деформации пружины 1 модели Максвелла, высокоэластической деформации модели Фойгта — Кельвина (пружина 4) и нарас­тающей во времени деформации вязкого элемента 2 модели Максвелла. Отсюда следует, что изменение упругих деформаций происходит в момент приложения внешней силы или при изменении ее, а затем она остается постоянной.

3. Явления переноса

Прикладная наука о транспортных явлениях рассматривает перенос массы, количества движения и энергии. Она включает в себя те теоретические правила, с помощью которых инженеры решают задачи, связанные с течением жидкостей, теплопереносом и диффу­зией в многокомпонентных средах. Ниже приводится краткий обзор законов переноса, поскольку процессы переработки полимеров включают в себя транспортные процессы.

Применительно к процессам течения вязкой жидкости эти уравнения формулируются следующим образом. Если выделить внутри занятого движущейся жидкостью объема произ­вольный элемент и ограничить его воображаемой замкнутой по­верхностью, то такой элемент будет представлять собой термоди­намически замкнутую систему (т. е. такую систему, которая мо­жет обмениваться с окружающей средой только энергией).

Отметим, что такие характеристики жидкости, как плот­ность , давление Р и температура Т, являются скалярными ве­личинами, скорость жидкости v - это величина векторная, а на­пряжение сдвига , возникающее в результате действия вязких сил, - симметричный тензор второго ранга.

Несмотря на компактность векторной формы записи, при ре­шении конкретных задач, связанных с исследованиями течения полимеров, приходится выбирать систему координат и определять в ней компоненты векторных и тензорных величин.

Ниже приведены уравнения неразрывности, движения и энер­гии, представленные в векторной форме, в прямоугольных (х, у, z) и цилиндрических (r, , z) координатах (рис. ).

Системы координат

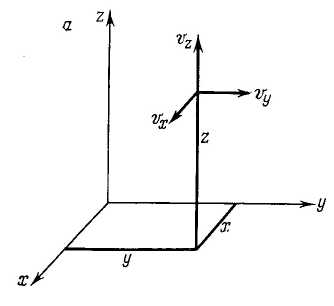
Рис. .