2.3. Обобщенная модель Максвелла.

При исследовании временной зави­симости напряжения при заданной деформации наблюдается яв­ление так называемой релаксации напряжений. Введем по анало­гии с упругим модулем в качестве характеристики любой полимер­ной системы так называемый релаксационный модуль G(t). Опре­делим релаксационный модуль как отношение мгновенного значения напряжения в испытуемом образце к величине деформа­ции, установленной при испытаниях в режиме постоянной дефор­мации. Тогда для тела Максвелла из выражения (2.9) имеем:

2.11

Сопо­ставление полученных характеристик тела Максвелла с характе­ристиками реальных полимеров, находящихся в высокоэластиче­ском состоянии, показывает, что между ними существует качест­венное сходство. Однако при попытке применения полученных математических зависимостей для количественного описания упруговязких характеристик реальных полимеров сразу же обна­руживается невозможность их непосредственного использования.

Наилучшее представление об этом дает анализ уравнения (2.11). Если взять натуральные логарифмы правой и левой частей уравнения (2.11), то получается:

2.12

Представим экспериментальные данные о релаксации напря­жений в координатах ln[G(t)/G] — f(t). В данном случае, если релаксационные свойства реаль­ного полимера можно было бы описать при помощи тела Мак­свелла, эти данные должны были бы уложиться на прямой. В дей­ствительности же релаксацион­ные свойства реальных полиме­ров изображаются кривой (рис. 2.6).

Кривые релаксации полимеров

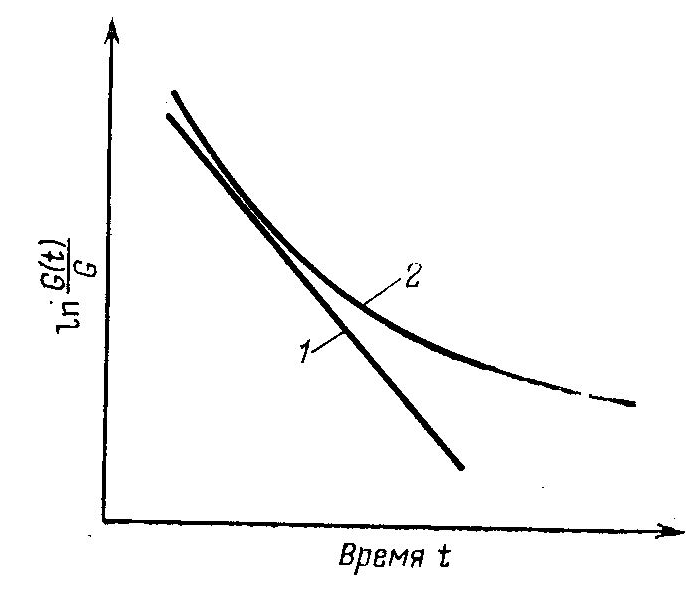
1 – тело Максвелла

2 – реальный полимер

Рис. 2.6.

Оказывается, что для того чтобы описать релаксационные свойства реальных полимеров, необходимо использовать модели, состоящие из ряда параллельно соединенных элементов Максвел­ла, каждый из которых характе­ризуется своим значением моду­ля упругого элемента G_i, и своим значением времени релаксации t_релакс (рис. 2.7).

Обобщенная модель Максвелла

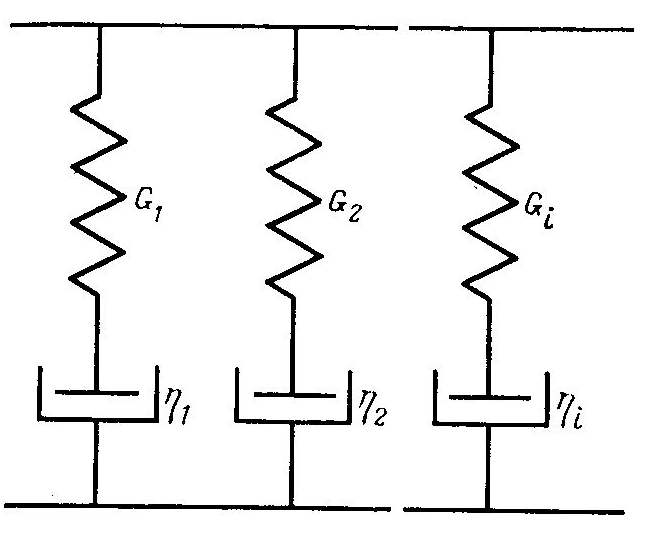
Рис. 2.7.

При этом чем больше число параллельно соединенных элементов Максвелла, тем точнее такая обобщенная модель описывает деформационные характеристики реального полимера.

2.13

Необходимость введения большого числа параллельно соеди­ненных элементов Максвелла для описания деформационных ха­рактеристик реальных полимеров является следствием сложности полимерной структуры и механизма деформации реальных поли­меров. Всякий реальный полимер представляет собой смесь поли­мерных молекул, обладающих разными значениями молекулярной массы и образующих различные надмолекулярные структуры, имеющие разную подвижность и соответственно разные значения времени релаксации. Аналогичным образом различны значения кинетической энергии теплового движения, запасенной отдельными участками полимерных молекул, и соответственно различны их упругие модули G_i. Стремление повысить точность описания свойств реальных полимеров за­ставляет все больше и больше увеличивать число элементов обобщенной модели Максвелла.

2.4. Модель Кельвина — Фойгта.

Модель Максвелла представляет собой наиболее общий механический аналог жидкости и позволяет удовлетворительно имитировать поведение линейных полимеров. С ее помощью удается наглядно описать релаксацию напряжений при заданной деформации.

Для моделирования поведения сши­тых полимеров, деформация которых ограничена существованием простран­ственной структуры, можно воспользо­ваться моделью, известной под названием модели Кельвина — Фойгта (рис. 2.8).

Модель Кельвина — Фойгта (а). Кинетика деформации (б).

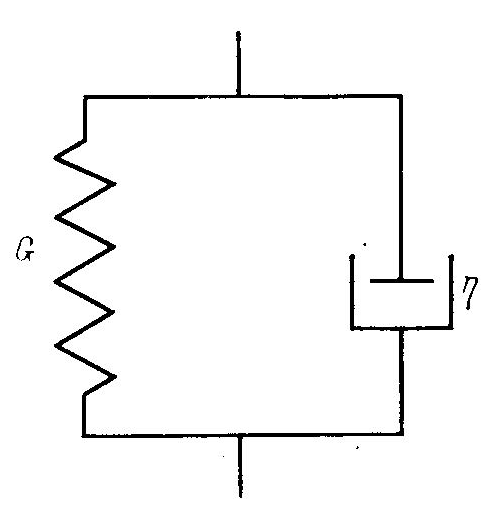
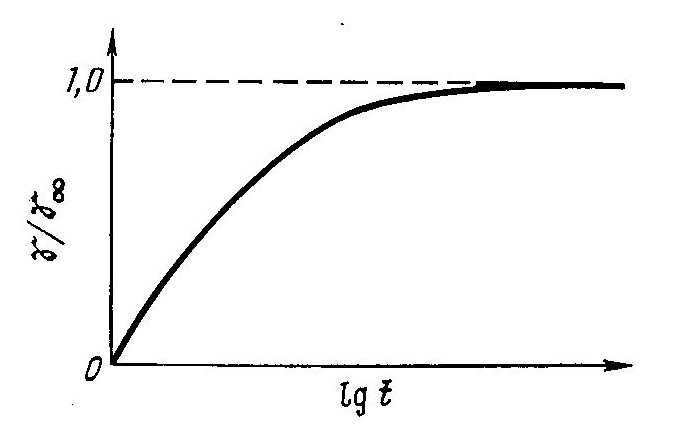
а б

Рис. 2.8.

Эта модель обладает свойствами твердого тела. Дифференциальное урав­нение модели Кельвина — Фойгта состав­ляется, исходя из условия, что деформа­ция упругого элемента модели равна де­формации ее вязкого элемента, т. е.

2.14

а суммарное напряжение в любой мо­мент складывается из напряжения, дей­ствующего в упругом и вязком элементах. Дифференциальное уравнение, описывающее поведение модели Кельвина —Фойгта, имеет вид

2.15

Рассмотрим решение этого уравнения для двух вариантов.

Первый вариант:

к телу Кельвина — Фойгта мгновенно прило­жена постоянная сила, вызывающая напряжение . При этом усло­вии решение уравнения (2.15) имеет вид

2.16

Величина  в данном случае является своеобразным аналогом времени релаксации и называется временем ретардации, или за­паздывания;  = /G.

Из уравнения (I. 43) видно, что равновесное значение деформа­ции для модели Кельвина — Фойгта, равное , не дости­гается сразу в момент приложения нагрузки, а требует для своего развития теоретически бесконечно большого времени (рис. 2.8 б). Физический смысл времени ретардации состоит в том, что по истечении промежутка вре­мени t —  деформация достигает 63% предельного значения.

Можно ввести характеристи­ку упругих свойств, так называемую податливость I, обратную модулю упругости:

2.17

Тогда уравнение (1.43) запишет­ся в виде:

2.18

Второй вариант, представляющий практический интерес, — это режим мгновенной разгрузки.

Пусть тело Кельвина — Фойгта сдеформировано силой, вызывающей напряжения , действие которой продолжалось в течение времени много большего, чем время запаздывания . Затем эта сила мгновенно снимается. Под действием запасенной в теле упру­гой энергии начнется процесс вос­становления. Процесс уменьшения деформации будет при этом описы­ваться уравнением

2.19

Уравнение (2.19) по форме подобно уравнению (2.9); про­цесс, описываемый этим уравнением, называется релаксацией деформации.

По аналогии с характеристиками, которые бы­ли введены для элемента Максвелла, можно получить соответ­ствующие вязкоупругие функции и для элемента Кельвина — Фойгта:

релаксационная податливость

2.20