1.6. Псевдопластичные (псевдовязкие) жидкости.

Для псевдопластичных жидкостей характерно уменьшение вязкости с увеличением скорости сдвига (рис. 1.6, кривая 2). В данном случае напряжение сдвига растет медленнее, чем скорость сдвига. К псевдопластичным жидкостям относятся некоторые суспензии, содержащие асимметричные частицы. Проявление аномалии вязкости, в данном случае уменьшение ее с ростом скорости сдвига, объясняется тем, что с увеличением скорости течения асимметричные частицы постепенно ориентируются. При этом вязкость убывает до тех пор, пока сохраняется возможность дальнейшего ориентирования частиц, а затем зависимость напряжения от градиента скорости становится линейной, т.е. в дальнейшем течет как ньютоновская жидкость.

Свойствами псевдопластичных жидкостей обладают также растворы и расплавы большинства полимеров. Однако для них аномалия вязкости обусловлена строением макромолекул, характером межмолекулярных связей и межмолекулярных образований, возникающих в расплаве. Для расплавов полимеров характерно также изменение степени аномалии вязкости в зависимости от скорости сдвига, т.е. интенсивность изменения вязкости при различных скоростях сдвига неодинакова. При высокой скорости сдвига вязкость уменьшается более значительно. Заметить это в обычных координатах ( )очень сложно, поэтому для анализа кривых течения применяют графическую зависимость, построенную в логарифмических координатах. Как видно из рис. 1.7, для ньютоновской жидкости характерна линейная зависимость lg  от lg с постоянным наклоном, равным 45°,(пунктирные линии). При уменьшении вязкости реологическая зависимость сдвигается вправо и вниз. Вязкость псевдопластичных жидкостей уменьшается от скорости сдвига, поэтому угол наклона линий меньше чем 45° и для описания реологических зависимостей применяют степенное уравнение:

 ^n-1 1.13

где n - показатель степени, характеризующий степень отклонения закономерности течения от ньютоновского закона; К - коэффициент, численно равный напряжению или вязкости жидкости при скорости сдвига, = 1.

С учетом степенной зависимости реологическое уравнение принимает вид:

 ⁿ 1.14

Преимущество степенного уравнения заключается в том, что оно содержит два коэффициента, которые легко определяются графически или аналитически по данным реологических исследований. Представим уравнение (1.14) в логарифмическом виде:

lg = lgK + nlg 1.15

Из этого уравнения видно, что К =  при = 1 , a n = tg, т.е. равен тангенсу угла наклона на логарифмической графической зависимости. Для ньютоновских жидкостей угол наклона равен 45°, а n = 1. Коэффициенты уравнения находятся из экспериментальных данных, полученных на вискозиметрах. Если зависимость в логарифмических координатах линейная, показатель степени можно рассчитать по формуле:

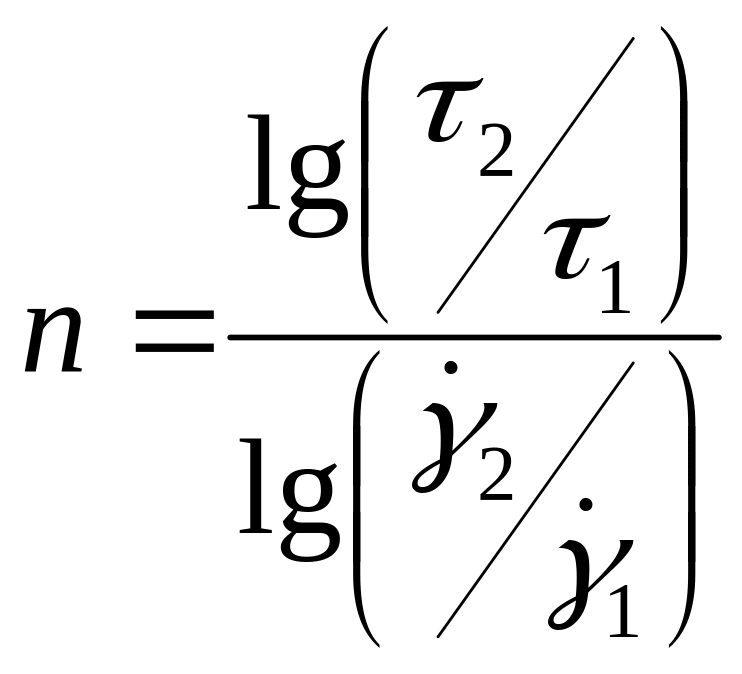1.16

где ₂ и ₁ — скорости сдвига, соответствующие двум точкам реологической

зависимости;

₂ , ₁ — напряжения сдвига при этих скоростях.

Реологические кривые для псевдопластичных жидкостей распо­лагаются под меньшим углом, чем ньютоновские жидкости. При этом, чем большей аномалией вязкости обладает жидкость, т.е. чем сильнее уменьшается вязкость от скорости сдвига, тем сильнее это отклонение и меньше угол наклона кривой.

В тех случаях, когда зависимость в логарифмических координатах не является линейной, показатель степени является переменной величиной. Для нахождения коэффициента K реологическую зависимость интерполирует на ось ординат при =1, а показатель степени в данном случае рассчитывается по уравнению:

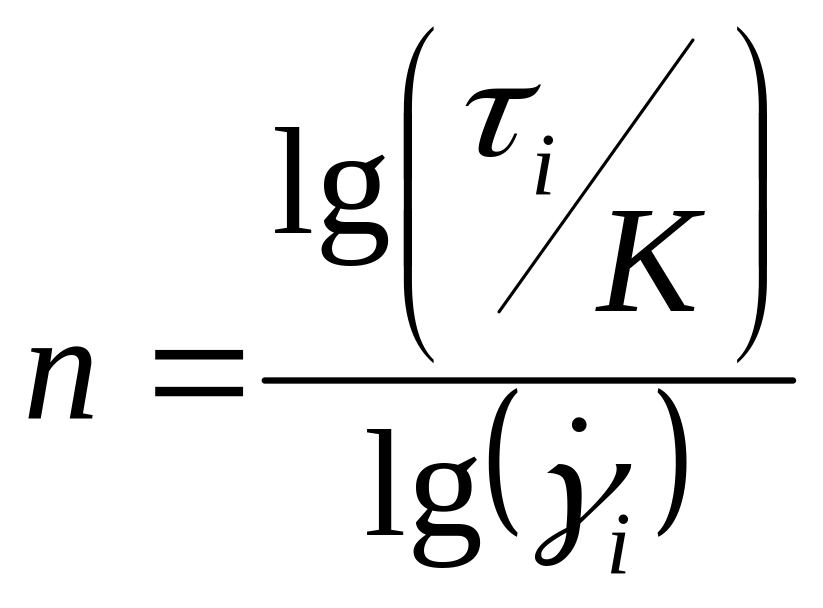1.17

где _i и _i — текущие значения напряжения и скорости сдвига, на реологической кривой.

Таким образом, в логарифмических координатах тангенс угла наклона кривой не пропорционален вязкости, а отражает лишь степень уменьшения вязкости от скорости сдвига. Жидкости с меньшей вязкостью смещаются вниз и вправо. Из сравнения кривых 2 и 4 на рис. 2.2 видно, что у первой жидкости (кривая 2) вязкость уменьшается в зависимости от скорости сдвига значительно сильнее, чем у второй, имеющей больший наклон и величину показателя степени.

Степень изменения аномалии вязкости системы отражается отклонением от прямолинейной графической зависимости. На рис. 1.7 видно, что такое изменение отсутствует для жидкости с прямолинейной зависимостью (кривая 4). Кривая 2 при малых скоростях сдвига идет параллельно прямой 1, что характерно для ньютоновской жидкости, а затем отклоняется. Это указывает на то, что для такой жидкости характерно наличие первой ньютоновской области, когда аномалия вязкости отсутствует, т.е. при малых градиентах вязкость постоянна и имеет максимальное значение. Такое значение называют наибольшей ньютоновской вязкостью и обозначают ₀ , т.е. значение вязкости при очень малых скоростях сдвига. Большинство растворов полимеров имеют две ньютоновские области (кривая 3), при этом вязкость для второй области обозначают _, т.е. вязкость соответствует большим скоростям сдвига. Таким образом, анализ реологических зависимостей в логарифмических координатах дает достаточно подробную качественную характеристику течения и широко используется для оценки реоло­гических свойств расплавов полимеров.

Графическое изображение реологи­ческих зависимостей вязких жидкостей в логарифмических координатах

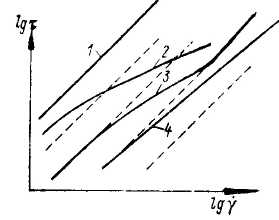
1— ньютоновская (угол наклона равен 45); 2 — псевдопластичная с одной ньютоновской областью течения; 3 — псевдопластичная с двумя ньютоновскими областями течения: 4 — псевдопластичная с малой вязкостью и постоянной степенью аномалии вязкости (линейная зависимость, n = const).

Рис. 1.7.