1.2. Понятие о скорости сдвига

Реология — наука, изучающая деформацию и течение в материалах под воздействием внешних сил.

При приложении внешних сил (например, гидростатического давления) или при движении поверхностей, контактирующих с расплавом полимера, возникает течение, основная особенность которого заключается в том, что одновременно развиваются три вида деформации: мгновенная упругая, высокоэластическая (запаздывающая упругая) и пластическая (необратимая).

Характер течения жидкостей оценивается с помощью зависимости напряжения сдвига от скорости сдвига или скорости деформации. Эта зависимость может быть представлена графически или в виде анали­тической функции — реологическим уравнением состояния. Приме­нимость его для анализа реологических свойств наиболее просто проследить на примере рассмотрения вязких жидкостей.

Вязкие жидкости по характеру течения, а точнее в зависимости от соотношения напряжения и скорости сдвига, подразделяются на четыре вида: ньютоновские, вязкопластичные, дилатантные и псевдопластичные (псевдовязкие). Для несжимаемых, вязких жидкостей реологическое уравнение состояния имеет вид:

_ij _ij 1.6

где _ij — компонента напряжения сдвига, Па;  — вязкость расплава. Паc; _ij — тензор скорости деформации.

Напряжение сдвига выражается величиной силы, действующей на единицу площади сдвига. Физический смысл скорости сдвига можно понять при рассмотрении простого течения жидкости. Если поместить жидкость между движу­щейся и неподвижной пластинами, расстояние между которыми равно h, то при течении возникает простой сдвиг, см. рис. 1.4 в. Скорость сдвига в этом случае будет равна:

dv_z /dy =v/y = v_пл /h 1.7

Таким образом, скорость сдвига, — это интенсивность изменения скорости одного слоя потока относительно второго, расположенного на некотором расстоянии у.

При одномерном сдвиге реологическое уравнение можно записать

 1.8

где — условное обозначение скорости сдвига.

Схема течения и эпюра скорости при течении жидкости за счет движения пластины (простой сдвиг).

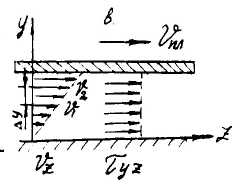
Рис. 1.4.

1.2. Деформация при течении полимеров

Существует большой класс жидкостей, у которых скорость сдвига увеличивается быстрее, чем напряжение сдвига. Графически из­менение скорости сдвига в зависимости от напряжения сдвига для жидкостей такого типа изобразится кривой 2 на рис. I. 6.

Вязкостные свойства таких жидкостей уже нельзя охарактери­зовать постоянной величиной. Можно по аналогии с ньютоновски­ми жидкостями считать, что в любой точке кривой 2 скорость сдвига по-прежнему определяется уравнением (1.9). При этом коэффициент вязкости утрачивает значение константы, а сам, в свою очередь, зависит от скорости (или напряжения) сдвига. В этом случае его принято называть эффективной вязкостью и обозначать _эф .

Жидкости, вязкость которых зависит от режима течения, при­нято называть аномально-вязкими жидкостями, а само явление — аномалией вязкости. Для аномально-вязких жидкостей чисто фор­мально можно представить связь между скоростью сдвига и на­пряжением сдвига в виде выражения

или 1.9

Графики, подобные представленным на рис. 1.5, обычно на­зывают кривыми течения.

Опыт показывает, что большинство полимеров и их растворов в условиях переработки обладает аномалией вязкости, что сильно усложняет задачу построения количественных теорий процессов переработки.

На полной кривой течения (см. рис. 1.5) можно выделить три характерных участка: начальный участок (область I), в пределах которого скорость деформации прямо пропорциональна напряже­нию сдвига (течение с наибольшей ньютоновской вязкостью); пе­реходной участок (область II), в пределах которого скорость де­формации возрастает быстрее, чем напряжение сдвига (эффек­тивная вязкость уменьшается с увеличением напряжения сдвига), и последний участок (область III), в пределах которого скорость деформации вновь растет пропорционально напряжению сдвига (течение с минимальной ньютоновской вязкостью).

Кривые течения, имеющие все три участка, удается наблюдать для полимеров. В случае расплавов обычно можно по­лучить только первые два участка.

Основная особенность течения полимеров заключается в одновре­менном развитии трех видов деформации: упругой _у, высокоэла­стической _в и пластической _п. Деформации первых двух видов носят обратимый характер, деформации третьего вида яв­ляются необратимыми. Таким образом, для деформации сдвига элементарной призмы, вырезанной из расплава, справедливо сле­дующее уравнение:

 = _у + _в + _п 1.10

Пластическая деформация представляет собой вязкое течение, связанное с необратимым перемещением молекул или их групп на расстояние, превышающее размеры самой молекулы. Скорость развития пластической деформации, так же как и высокоэластиче­ской, сильно зависит от температуры.

Одновременное развитие всех этих трех видов деформации при­водит к тому, что в условиях установившегося течения полимеры обладают свойствами так называемых аномально-вязких, или не­ньютоновских жидкостей. Это означает, что при весьма малых напряжениях сдвига реологические свойства расплава характери­зуются постоянной ньютоновской вязкостью. В этой области ско­рость накопления высокоэластиче­ских деформаций оказывается мень­ше скорости их релаксации, быстро увеличивающейся с ростом дефор­мации. Вследствие этого накоплен­ная обратимая деформация оказы­вается очень малой, а материал течет с постоянной ньютоновской вязкостью  (область I на рис. 1.5). Дальнейшее увеличение напряже­ния (или скорости деформации) приводит к тому, что накапливаю­щаяся деформация уже не успевает релаксировать полностью, поэтому какая-то часть деформации носит высокоэластический характер. Внеш­не это проявляется в интенсивном уменьшении сопротивления деформации или, иначе говоря, в уменьшении коэффициента вязкости системы (область II на рис. 1.5). Наконец, если скорость дефор­мации настолько велика, что высокоэластическая деформация по­лимерных молекул остается неизменной, то коэффициент вязкости перестает уменьшаться, достигая некоторого минимального значе­ния _ (область III на рис. 1.5).

Кривая течения аномально-вязкой жидкости.

Рис. 1.5.