11.3. Течении расплавов полимеров в кольцевых каналах

При течении расплавов полимеров в кольцевых каналах изменение закономерности коэффициента восстановления струи в зависимости от длины канала, температуры и скорости сдвига сохраняются, однако в данном случае одновременно с увеличением наружного диаметра экструдата увеличивается и толщина стенки. При этом на значение эластического восстановления влияет соотношение внутреннего и наружного радиусов канала: чем меньше величина R_B /R_H, тем больше разбухание, см. рис.2.23.

Зависимость коэффициента эластического восстановления от отношения диаметров кольцевого канала:

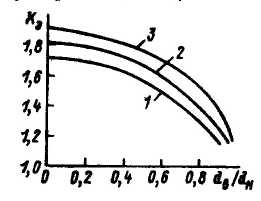
1 — полипропилен; 2 — полиэтилен низкой плотности;

3 —полиэтилен высокой плотности.

Рис.2.23.

При близких значениях R_B и R_H наружный размер заготовки увеличивается, а внутренний уменьшается почти одинаково, т.е. конформационные переходы происходят одновременно

за счет увеличения диаметра и толщины стенки. В том случае, когда диаметр дорна мал, увеличение заготовки происходит преимущественно по наружному диаметру (рис. 2.23). Такое непропорциональное изменение размеров объясняется тем, что деформация и нормальное напряжение для цилиндрических оболочек пропорциональны радиусам. Зависимость коэффициентов эластического восстановления струи при выходе расплава из кольцевого канала может быть выражена следующим уравнением:

где — коэффициенты восстановления струи по среднему радиусу и толщине стенки экструдата.

Изменение размеров экструдата (а) и схема возникновения тангенциальных и нормальных напряжений _(6) при течении между, вращающимися цилиндрами.

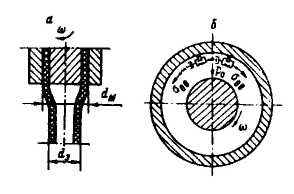
Рис. 2.24.

Схема расположения векторов напряжений при круговом течении расплава

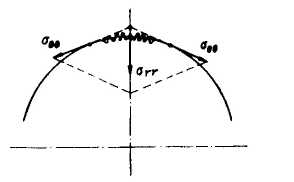
Рис. 2.25.

В значительной степени картина проявления эластического восстановления струи изменяется при наложении на осевые напряжения сдвига тангенциальных напряжений. Этого можно достигнуть, например, при вращении одного из цилиндров кольцевого канала. В данном случае, если тангенциальные напряжения очень малы, то изменение размеров экструдата происходит, как и при одноосном течении, т.е. наблюдается увеличение диаметра. При больших значениях _, когда достигается определенное отношение _zz/_ расплав на выходе уменьшается в диаметре (рис. 2.24).

Под действием кругового течения макромолекулы полимера ориен­тируются и располагаются в кольцевых слоях сдвига, что показано в виде модели на рис. 2.24 б. Так как векторы нормальных сил _ расположены под некоторым углом (по дуге окружности), возникает нормальное радиальное напряжение и соответственно появляется составляющая силы, стягивающая расплав к оси вращения, т.е. трубчатая заготовка уменьшится в диаметре. Однако под действием нормальных осевых напряжений _zz проявляется противодействие уменьшению диаметра экструдата. Поэтому в зависимости от соотношения величин этих напряжений происходит сужение или расширение струи. Если осевые напряжения велики, то происходит разбухание, а если больше тангенциальные, то сужение струи. Зависимость между коэффициентами эластического восстановления струи и нормальными напряжениями имеет вид:

Или, переходя от нормальных напряжений к касательным, получаем:

Экспериментальные и расчетные данные имеют хорошую сходимость, (отклонение составляет 2 — 5 %). Поэтому полученные уравнения можно применять для расчета скорости течения или размеров каналов при производстве пустотелых изделий, профилей и гранул. Исходя из условия обеспечения заданных размеров изделий, т.е. по известным размерам формующей головки и значению Кэ, можно рассчитать размеры выходящего экструдата. По данным уравнениям решается также обратная задача, т.е. определяются размеры формующих каналов при известных условиях течения расплава и заданном значении Кэ.