11. Специфические эффекты при течении полимеров

Наличие конформационных переходов при течении, а также развитие упругой деформации обусловливают появление специфических эффектов, характерных для течения расплавов и растворов полимеров, таких, как возникновение нормальных напряжений при сдвиговом течении, эффекта Барруса и эффекта Вайссенберга.

11.1. Развитие нормальных напряжений.

При течении расплава под воздействием напряжений сдвига макромолекула подвергается силовому воздействию. Поскольку одна часть макромолекулы задерживается межмолекулярным взаимодействием, а другая ее часть увлекается в дви­жение, то происходит ориентация. В то же время тепловая флуктуация вызывает частичную дезориентацию макромолекул, поэтому в зависимости от скорости сдвига и температуры устанавливается динамическое равно­весие. Однако в целом ориентированное состояние является неравно­весным, поэтому вдоль основной цепи возникает усилие, обусловливающее появление нормальных напряжений. Значение этих напряжений пропорционально напряжению сдвига и накопленной упругой деформа­ции. Обычно подобные зависимости записывают относительно разности нормальных напряжений. Так, в случае осевого течения в цилиндри­ческом канале первую разность нормальных напряжений можно вычис­лить по формуле Вайссенберга - Муни — Ривлина:

_zz - _rr = _rz _у

При очень малых упругих деформациях применяют формулу Лоджа:

_zz - _rr = 2_rz _у

Подобные уравнения применяют соответственно при течении в плоско-щелевых и прямоугольных каналах.

Относительно второй разности нормальных напряжений существуют различные мнения. Некоторые авторы считают, что _rr - _  0. Однако указывается также, что эта разность значима, но имеет отрицательную величину.

Упругая деформация, возникающая при сдвиговом течении, зависит от напряжения сдвига и описывается уравнением:

где G()- модуль упругости, который является функцией градиента скорости или напряжения сдвига.

11.2. Эффект Барруса.

После выхода расплава из формующих каналов под действием нормальных напряжений возникает эластическое восстановление струи, так называемый эффект Барруса. Эластическое восстановление — это изменение сечения и геометрической формы экструдата. Так, при течении в цилиндрическом канале на выходе наблюдается увеличение диаметра, а при истечении из кольцевых каналов изменяется как диаметр, так и толщина стенки трубчатого экструдата (рис. 2.20). Кроме этого при изготовлении сложных профилей и при наличии неоднородности напряжений сдвига в отдельных частях формующего канала очень сильно изменяется геометрия профиля.

Изменение размеров расплава после выхода из канала

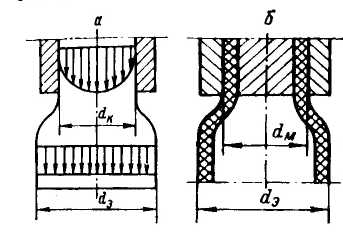
а — круглый профиль; б — трубчатая заготовка.

Рис. 2.20.

В качестве показателя эластичес­кого восстановления используют коэффициент К_э :

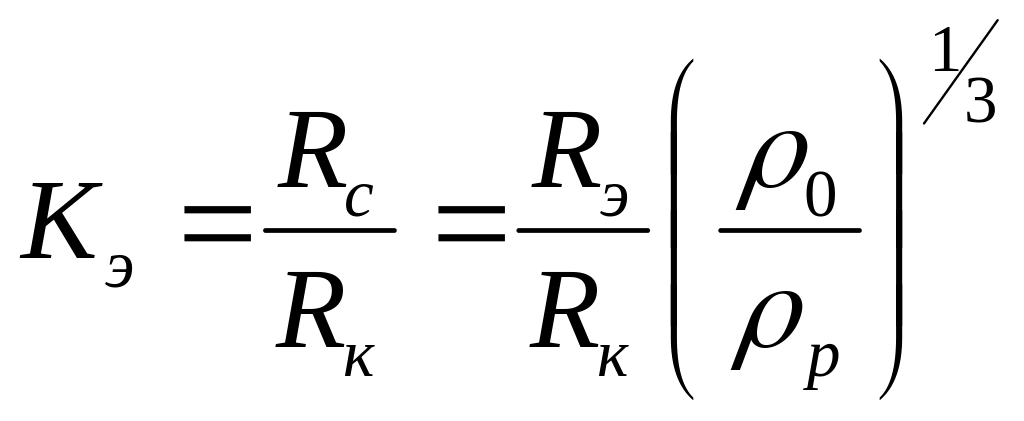
где R_c - радиус струи расплава; R_э - радиус экструдата после охлаждения; R_к - радиус формующего канала; _р - плотность расплава; ₀ - плотность полимера при 20°С.

Изменение линейных размеров экструдата (уменьшение длины и увеличение сечения) связано с протеканием релаксационных процессов. Упругая деформация, накопленная в расплаве при течении в канале, восстанавливается после снятия внешней силы, т.е. макромолекулы при выходе из канала переходят в равновесное состояние. Однако этот процесс происходит при свободном выходе. Когда же расплав отводится с помощью тянущего приемного устройства, то он на выходе за счет принудительной вытяжки подвергается действию растягивающих напря­жений и, если эти напряжения больше нормальных, обусловленных напря­жениями сдвига, то сечение экструдата уменьшается. В дальнейшем мы будем рассматривать процесс со свободным выходом расплава из фор­мующего канала.

Поскольку ориентация макромолекул количественно связана с напря­жением сдвига, то коэффициент эластического восстановления зависит от скорости сдвига, температуры и длины канала. При увеличении скорости сдвига происходит нелинейный рост коэффициента эласти­ческого восстановления (рис. 2.21). При низких температурах высокая степень ориентации достигается при малых значениях скорости сдвига, а при повышении температуры зависимость становится более плавной, так как возрастает процесс дезориентации макромолекул под действием тепловой флуктуации.

Зависимость коэффициента эластического восстановления от ско­рости сдвига для полиэтилена низкой плотности при различных температурах.

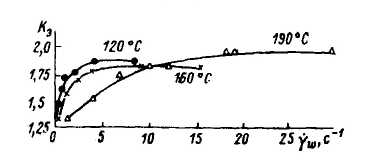
Рис. 2.21.

Следует заметить, что при достижении некоторого значения скорости сдвига темп роста коэффициента эластического восстановления К_э замедляется, а в некоторых случаях даже уменьшается. Это явление связано с образованием больших напряжений сдвига, появлением эластической турбулентности, т.е. проскальзыванием расплава по поверхности канала.

При увеличении длины канала К_э снижается, что объясняется наличием входовых потерь давления. Поскольку на входе в канал развиваются большие напряжения сдвига, то при течении в коротких каналах они не успевают снизиться к выходу, т.к. режим течения не переходит в установившийся. В этом случае расплав вытекает с большой степенью ориентации, поэтому коэффициент эластического восстанов­ления больше, чем в длинных каналах. При увеличении длины канала напряжения постепенно снижаются, и на некотором расстоянии от входа расплав в канале переходит к установившемуся режиму течения, поэтому напряжения становятся минимальными. Высокая степень ориентации, достигнутая на входе, постепенно к выходу из канала уменьшается, что снижает значение коэффициента "разбухания" струи (рис. 2.22). При дальнейшем увеличении длины канала коэффициент разбухания остается постоянным.

Зависимость изменения коэффициента эластического восстановления струи от длины канала при различных скоростях сдвига.

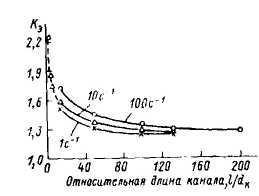
Рис. 2.22.

Используя аналогичный анализ, можно предсказать изменение К_э от других факторов, влияющих на реологические характеристики. Основным критерием оценки эластического восстановления должны служить напряжение сдвига и время релак­сации. Так, применение конического участка на входе в канал позволяет значительно снизить К_э. В этом случае увеличение коэффициента будет наблюдаться до более высоких скоростей сдвига, поскольку напряжения сдвига на входе уменьшаются и неустойчивое течение, т.е. срыв струи, сдвигается в область больших напряжений сдвига.

Для математического описания процесса эластического восстанов­ления струи принимаем следующие условия:

1) на выходе расплава из канала сохраняется изотермичность потока;

2) считаем, что гравита­ционные силы, действующие на расплав, незначительны (масса выдавленного полимера мала);

3) жидкость не сжимаемая;

4) течение в канале установившееся;

5) время эластического восстановления велико и достаточно для осуществления процесса релаксации напряжений на выходе из канала.

Если на расплав действует нормальное напряжение _zz, равномерно распределенное по сечению канала, то накопленная упругая и высокоэластическая деформация струи будет равна:

где Е - модуль упругости при сжатии; _zz - среднее значение нормальных напряжений.

Однако накопленная упругая деформация восстанавливается не полностью, поскольку часть нормальных напряжений уравновешивается гидростатическим давлением, которое создается внутри струи на выходе после эластического восстановления. Это обусловлено следующими факторами.

При сдвиговом течении в каналах возникают неоднородные напряжения сдвига, которые являются функцией радиуса или глубины канала (см. разделы 2.3 и 2.5). Возникающая под действием напряжения сдвига ориентация макромолекул также изменяется по глубине канала. При этом в центре она минимальна, а на поверхности канала имеет максимальное значение. При эластическом восстановлении растянутые внешние слои сжимают расплав и внутри струи возникает избыточное давление, под действием которого внешние слои расплава растягиваются в тангенциальном направлении. Таким образом, внешние слои экструдата при эластическом восстановлении можно рассматривать как упругую цилиндрическую оболочку, находящуюся под давлением. Из теории прочности цилиндрических оболочек следует, что равновесие при деформации оболочки наступает, когда

2_ост = _

Таким образом, упругая осевая деформация (сжатие струи и разбухание) будет происходить до момента установления в расплаве равновесия осевых и вновь возникших тангенциальных напряжений. После разбухания струи часть упругой накопленной деформации остается в расплаве, создавая _ост. Поэтому можем записать:

_ост = _zz - _упр

где _ост — нормальные напряжения, действующие в направлении оси z после упругого восстановленя струи; _упр - напряжения, израсходованные на разбухание струи расплава. Используя уравнение первой разности напряжений и связь упругой деформации с напряжением сдвига,

_zz - _rr = _rz _у, а _у = _rz / G

а также считая, что нормальные радиальные напряжения _rr в поверхностных слоях струи равны нулю, получаем:

_zz = _rz² / G_

При расчетах, текущее значение напряжений сдвига лучше заменить на напряжение, возникающее на поверхности канала, тогда из равенства осевой силы, получаем:

_zz = 4_rz² / 9G_

Напряжение, которое расходуется на упругое восстановление струи, можно определить из закона Гука, _упр = Е, а для расчета упругой деформации восстановления запишем равенство:  = (l₁ – l₂)/l₂, где l₁ и l₂ - длина экструдата до и после эластического восстановления струи. Из закона сохранения массы расплава можем записать:

l₁R_k² = l₂R_э²

Откуда получаем:

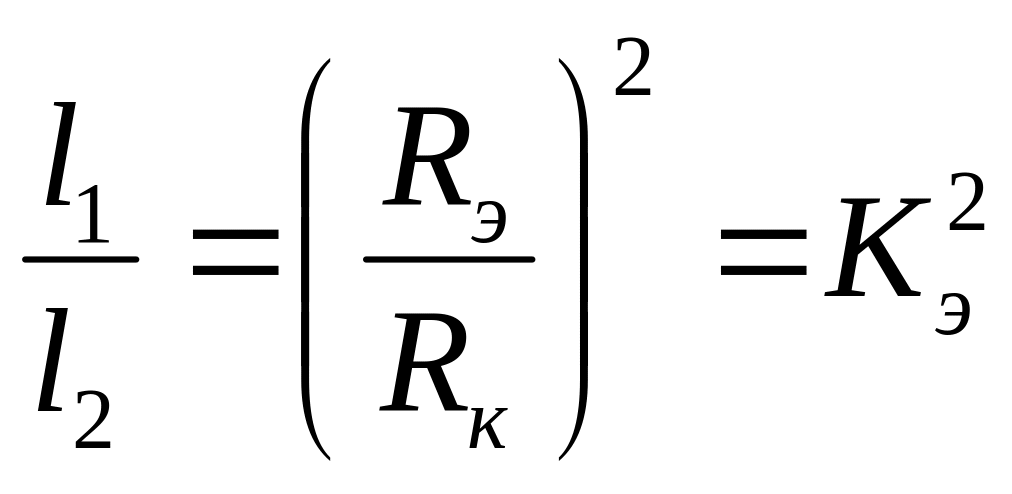
С учетом рассмотренных уравнений, находим:

Нормальное напряжение, возникающее в тангенциальном направле­нии связано с напряжением восстановления упругой деформации, равенством:

где  - коэффициент Пуассона расплава полимера.

Подставив полученные значения напряжений в уравнение (2.89), и с учетом равенства (2.88) после преобразования, находим:

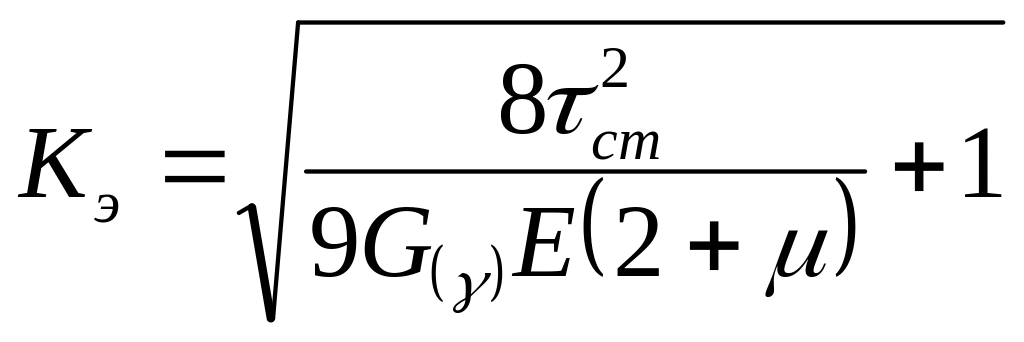
Таким образом, полученное решение учитывает восстановление упругой деформации струи расплава, имеющую неоднородную степень ориентации макромолекул полимера по сечению и уравновешивание остаточных напряжений, тангенциальными напряжениями, возникающими при разбухании и изменение напряжений по длине канала.

Данное уравнение получено для канала сравнительно большой длины. Поэтому при переходе к коротким каналам необходимо учесть напря­жения, возникающие на входе в канал, и их частичную релаксацию. Используя уравнение (2.78), полученное для модели Максвелла, можем определить напряжения сдвига при течении в коротких каналах:

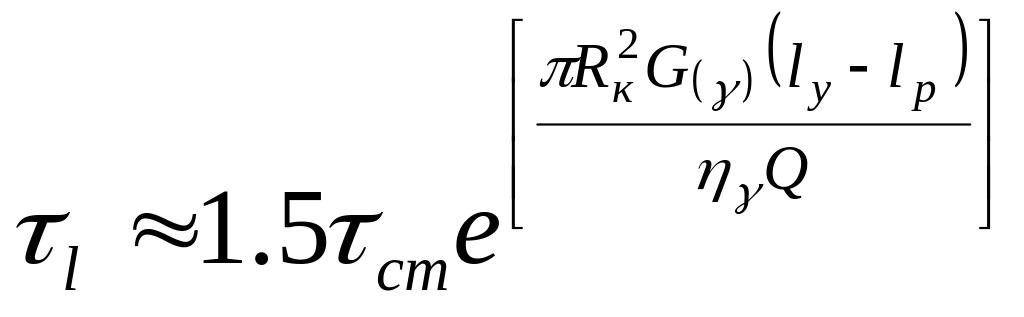
где l_у — длина канала, в котором развивается установившееся течение; l_p — длина рассчитываемого канала; Q — объемный расход расплава; _cт — напряжение, соответствующее установившемуся течению.

С учетом экспериментальных данных (см. рис. 2.22) можно с некоторым приближением принять Д. = 200R. Подставляя величину ъ. в уравнение (2.95), можно рассчитать коэффициент эластического восста­новления для канала любой длины.

Используя рассмотренные уравнения и экспериментальную величину коэффициента эластического восстановления, а также равенство

_zz - _rr = G_ _у²

(где _у — упругая деформация), можно получить уравнение для расчета первой разности нормальных напряжений, возникающей при течении в цилиндрических каналах:

Другие авторы, в частности Мендельсон, Фигнер и Бэгли, неод­нородную степень ориентации учитывают только усреднением усилий, возникающих от действия нормальных осевых напряжений, что справедливо для упругих тел, а не для расплавов полимеров, которые подвергаются сдвиговому течению и имеют неоднородную ориентацию макромолекул.