8. Капиллярная визкозиметрия. Входовые эффекты.

Рассмотрим движение расплава в цилиндрическом канале срав­нительно небольшой длины с радиусом R. Расплав поступает из канала большого сечения и течет под действием перепада давления, создаваемого по длине канала (рис. ).

При переходе расплава из большого резервуара в канал небольшого сечения происходит сравнительно быстрое изменение скорости, которая стабилизируется на некотором удалении от входа. Отдельные авторы считают, что вначале профиль скорости имеет почти прямоугольную форму, однако эксперименты, выполненные на прозрачных каналах при течении с контрастным наполнителем, этого не подтверждают. Формо­вание профиля начинается перед входом за счет образования в расплаве конического гидродинамического конфузора, как показано на рис. 2.14. Центральная струя имеет наибольшую скорость, которая уменьшается по мере удаления от оси канала и, если канал имеет прямоугольный вход, то в углах могут образоваться циркуляционные потоки (вихревые зоны).

Как уже было рассмотрено ранее, под действием напряжений сдвига в расплавах полимеров может происходить разрушение структуры и изменение конформации макромолекул, т.е. течение сопровождается развитием упругой деформации. Поскольку на входе в канал скорость изменяется по длине, т.е. имеется градиент скорости (dv_z/dz)0, то упругая деформация постоянно возрастает. При увеличении скорости течения расплава полимера повышается степень разрушения структуры и уменьшается число пространственных узлов.

Изменение давления по длине канала при неустановившемся течении расплава: неустановившееся течение dp/dz  const; установившееся течение dp/dz = const.

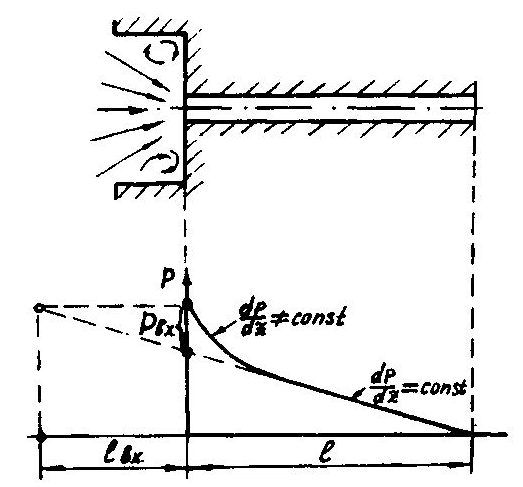
Рис. .

Поскольку все эти процессы протекают не мгновенно, то завершаются они с неко­торым отставанием от темпа развития ско­рости. Следовательно, по мере течения расплава по длине канала изменяется напря­жение сдвига и меняется доля энергии, за­трачиваемая на развитие упругой деформации и разрушение структурных элементов системы. На входе в канал затрата энергии максимальна, а затем она постепенно уменьшается и при переходе к установившемуся режиму энергия расходуется лишь на развитие вязкого течения. Часть затраченной на входе энергии пере­ходит в теплоту, а другая часть в виде потенциальной энергии (накопленная упругая деформация) сохраняется в расплаве и реализу­ется на выходе из канала при разбухании струи. Такое неравномерное потребление энергии вызывает непропорциональные потери давления по длине канала.

Таким образом, канал, в зависимости от режима течения, можно разбить на два участка. Первый — участок входа, когда (dp/dz)const, на котором потери давления зависят от трех составляющих:

1) неустано­вившееся течение в сходящемся потоке на входе в канал,

2) вязкие потери при перестройке профиля скорости потока,

3) развитие упругих дефор­маций.

Второй — участок с установившимся течением при (dp/dz)=const, где перепад давления обусловлен преимущественно вязкими потерями при течении расплава. Если решение для неустановившегося течения выполняется с учетом входовых потерь и проявления упругих деформаций, то в реологическое уравнение необходимо ввести дополни­тельные компоненты, описывающие вязкоупругие свойства и инерционные силы. То есть в уравнениях движения необходимо учесть целый ряд дополнительных членов: dv_z/dz, d_zz/dz и dp/dz = f(z), что очень затрудняет решение.

Для инженерных расчетов целесообразнее использовать косвенныйграфо-аналитический метод, для чего процесс течения рассматриваемкак установившийся, а непропорциональное изменение давления заменяем линейной функцией с введением поправочного входового коэффициента р_вх или l_вх (см. рис. ). В данном случае общий перепад давления заменяем суммой:

где dp/dz - градиент давления; l - длина канала; р_вх - потери давления на входе; р_l, р_о - давление на входе и выходе из канала.

Таким приемом мы как бы искусственно все дополнительные затраты энергии на входном участке сосредотачиваем на входе в канал и сводим решение задачи к установившемуся режиму течения, когда

Для цилиндрического канала:

Для плоскощелевого канала:

где р = р_l - р₀

Приведение к установившемуся течению можно выполнить также вторым способом. Продолжим пропорциональную зависимость распре­деления давления влево от оси ординат до пересечения с линией давления, равного р_г При этом мы искусственно удлиняем канал на величину l_вх (см. рис. ), и течение заменяем установившимся. В этом случае напряжения сдвига будут равны:

Для определения скоростей сдвига пригодны уравнения (2.41) и (2.63).

Обычно для удобства расчетов вместо l_вх используют входовой поправочный коэффициент т:

т = l_вх /R или l_вх =mR (l_вх = ND – поправка Бэгли)

Поскольку входовые потери связаны с развитием вязкоупругих дополнительных деформаций и разрушением структуры, то они зависят от скорости сдвига и температуры.

Для экспериментального определения входовых потерь давления или поправочного коэффициента обычно используют каналы (сопла) различной длины, но одинакового диаметра. Измеряют последовательно зависимость давления от объемного расхода при течении в каналах различной длины и строят график (рис. 2.16). Затем находят давления на входе в канал при постоянных расходах для каждой длины (горизонтальные сечения). Определив р₁, р₂ и р_з строят графическую зависимость изменения давления от длины канала. Если длина наиболее короткого канала больше, чем длина входового участка с неустановившимся течением, то получаем линейную зависимость (рис. 2.17). Интерполируя полученную линейную зависимость на ось ординат, находим значение давления p_вх для различных расходов (скоростей сдвига). Для слишком коротких каналов линейной зависимости не получается, поэтому такой метод определения входных потерь использовать нельзя.

Если проинтерполировать полу­ченную зависимость до пересечения с осью абсцисс, то отсекаемые отрезки будут численно равны поправочному

коэффициенту т =l_вх / R.

Графическую зависимость, показанную на рис. 2.16, можно исполь­зовать также для расчета напряжения сдвига третьим способом. У каналов с одинаковыми радиусами и с постоянным объемным расходом расплава, скорость сдвига и входовые потери также будут постоянными. Поэтому для каналов различной длины, можем записать:

;

Решая совместно эти уравнения и считая, что ₁ = ₂ при Q₁ = Q₂, находим:

Зависимость давления от длины канала, используемая для нахож­дения входных потерь.

Рис. 2.17.

Зависимость объемного расхода от давления при различной длине канала (l₂ > l₁).

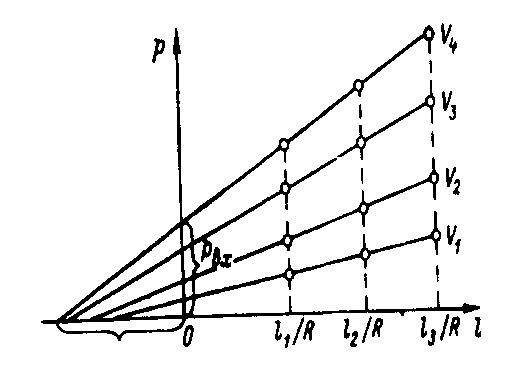
Рис. 2.16.

Таким образом, подставив значения давлений р₁ и р₂, найденные из графика рис. 2.16, мы можем найти изменение напряжения сдвига от скорости сдвига для различных расходов.

Полученные уравнения применяются для обработки данных капил­лярной вискозиметрии, а также для нахождения перепада давления (обратная задача) при течении расплавов полимеров в формующих экструзионных головках или в литниковых каналах формы при литье под давлением. Применяются они в тех случаях, когда при переходе от одного канала к другому имеется резкое сужение канала или его резкий поворот.

9. Ротационная вискозиметрия

9.1. Вискозиметры конус - конус, конус - плоскость

9.2. Вискозиметры коаксиальные цилиндры

10. Практические методы количественного описания аномалии вязкого течения

Большинство расплавов обладает свойствами аномально-вязких жидкостей. Представим зависимость скорости сдвига от напряжения сдвига в обычных координатах. Если расплав обладает свойствами ньютоновской жидкости, то в этих координатах его кривая течения изображается прямой с угловым коэффициентом, равным 1/, где  - ньютонов­ская вязкость. Если же расплав обладает свойствами аномально-вязкой жидкости, то его кривая течения выгнута по направлению к оси напряжений. Это означает, что каж­дой точке этой кривой соответствует свое значение эффективной вязкости, численно равное единице, деленной на угловой коэффициент прямой, проходящей через начало коорди­нат и соответствующую точку кривой.

Для полного суждения о реологических свойствах расплава надо представлять себе его кривую течения при изменении скорости сдвига в диапазоне 3—4 десятичных порядков. Поэтому экспери­ментальные данные представляют в логарифмических координа­тах. В том случае, если масштабы, выбранные для оси абс­цисс и для оси ординат, одинаковы, системам, обладающим свой­ствами ньютоновских жидкостей, будут соответствовать прямые, наклоненные к осям под углом 45°. При этом абсолютная величина вязкости сказывается только на месте расположения прямой.

Кривые течения

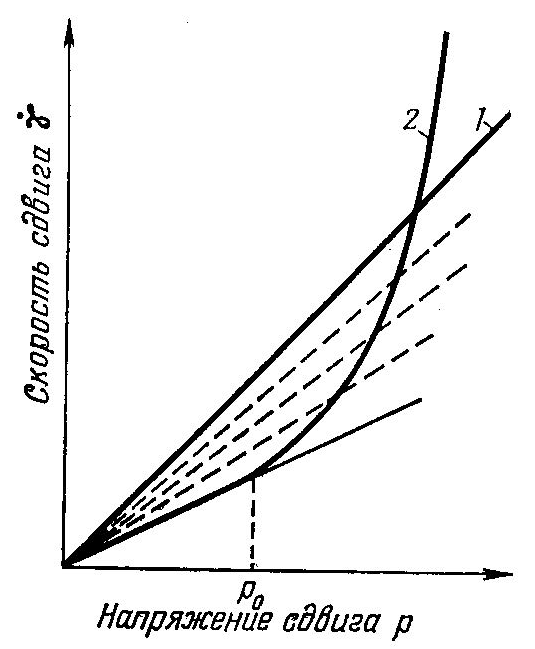
1 – ньютоновская жидкость,

2 – аномально-вязкая жидкость

рис. .

Кривые течения реальных расплавов в логарифмических коор­динатах слабо изогнуты. Обратим внимание на то, что для псевдо­пластичных жидкостей значение производной в любой точке этих кривых больше единицы. Это условие записывается в виде нера­венства

Значение производной позволяет легко оценивать степень ано­малии вязкого течения. Выше мы отмечали, что для ньютоновских жидкостей производная равна единице. Чем больше аномалия вяз­кости расплава, тем больше значение производной. Для расплавов термопластов и эластомеров производная в преде­лах одной кривой может изменяться от 1 до 5.

Слабая кривизна логарифмических кривых течения явилась причиной того, что наиболее широко для их математического опи­сания применяется так называемый степенной закон, имеющий вид

или

где n' = 1/n.

Обычно экспериментатор располагает данными о зависимости напряжения сдвига от скорости сдвига при изменении последней в пределах 2—3 десятичных порядков. Если обследованная область достаточно далеко отстоит от области ньютоновского течения, то логарифмическая кривая течения легко аппроксимируется прямой:

Значение n, по определению, равно производной для соответ­ствующего участка логарифмической кривой течения:

Поскольку величина n характеризует аномалию вязкости, она получила название индекса течения.

Для ньютоновской жидкости величина  имеет смысл вязкости. Для аномально-вязких жидкостей величина  не имеет столь чет­кого физического смысла. Она является своеобразным аналогом вязкости и обычно называется коэффициентом консистенции.

Известны и более сложные способы описания кривых течения. Трехпараметрическое степенное уравнение:

Здесь ₀ - предельное значение вязкости, соответствующее об­ласти ньютоновского течения при минимальных напряжениях сдвига. В области малых напряжений сдвига уравнение вырождается в закон Ньютона и хорошо описывает начальный участок кривой течения.

В области высоких напряжений сдвига доминирующее значе­ние приобретает второй член, и уравнение фактически превра­щается в обычный степенной закон. Наконец, в области переход­ных напряжений оба члена оказываются соизмеримыми, и уравне­ние удовлетворительно описывает участок с переменным индексом течения.

При необходимости увеличить точность аппроксимации кривой течения приходится прибегать к еще более сложным зависимостям.

В качестве примера сошлемся на четырехпараметрическое уравне­ние:

,

где ₀ — ньютоновская вязкость, соответствующая начальному участку кривой течения; k₁, k₂ и n - эмпирические константы, определяемые обработкой экспе­риментальных данных.