6. Изотермическое установившееся течение аномально вязких жидкостей между вращающимися цилиндрами

Рассмотрим движение расплава, вызванное вращением внутреннего цилиндра вокруг своей оси с угловой скоростью со, когда перепад давления по оси z отсутствует. Для вывода уравнений течения принимаем те же допущения, что были приняты при решении задачи для течения в цилиндрическом канале.

Схема течения показана на рис. **. Канал образуется внутренним цилиндром с радиусом R₁ и внешним цилиндром с радиусом R₂.

Поскольку осевое течение отсутствует, члены уравнений ****, содержащие _rz будут равны нулю, а действующим будет напряжение _r, возникающее на концентрических поверхностях, перпендикулярных к радиусу.

Проекция на направление r

Проекция на направление 

Проекция на направление z

Так как перепады давления отсутствуют, то соответственно имеем:

Проанализировав уравнения движения, как было проделано в разделе 2.4, получаем:

После интегрирования этого выражения имеем:

Схема течения расплава между вращающимися цилиндрами.

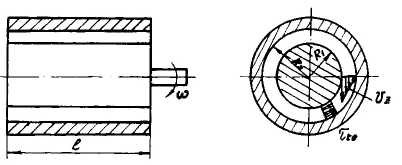
Рис. **.

Реологическое уравнение для данного случая течения с учетом уравнений (2.16), (2.20) и (2.22) имеет вид:

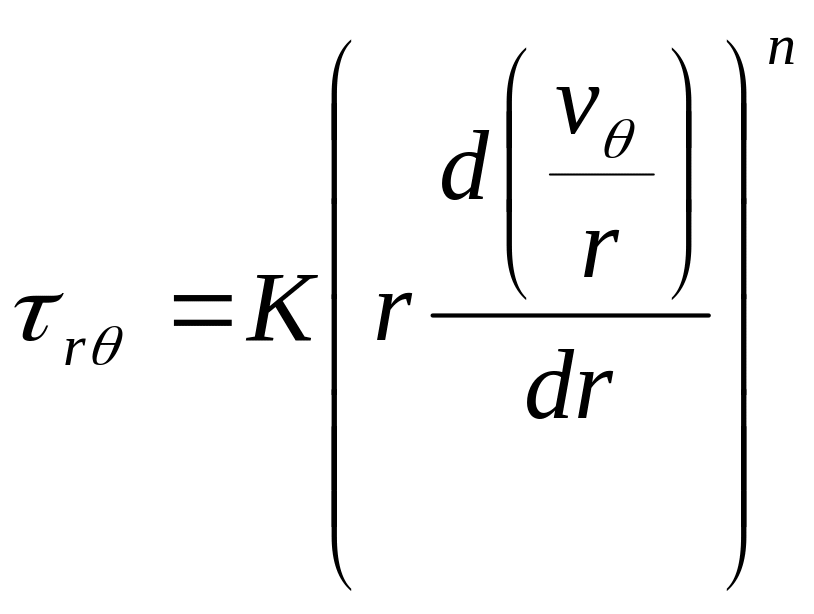
Подставив это выражение в уравнение (2.43) имеем:

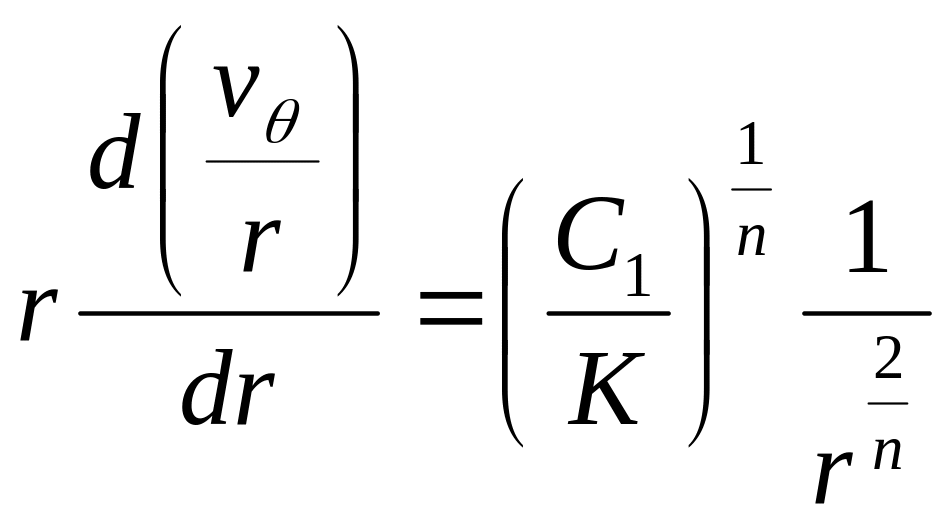
К) г 56

Разделив оба члена уравнения на г и проинтегрировав, получаем:

Заменив выражение новой постоянной

после подстановки ее в (2.45), имеем:

Постоянные интегрирования находим из условий:

при , ; ,

Подставив эти значения в уравнение (2.47), получаем:

,

Решив совместно эту систему уравнений, находим:

,

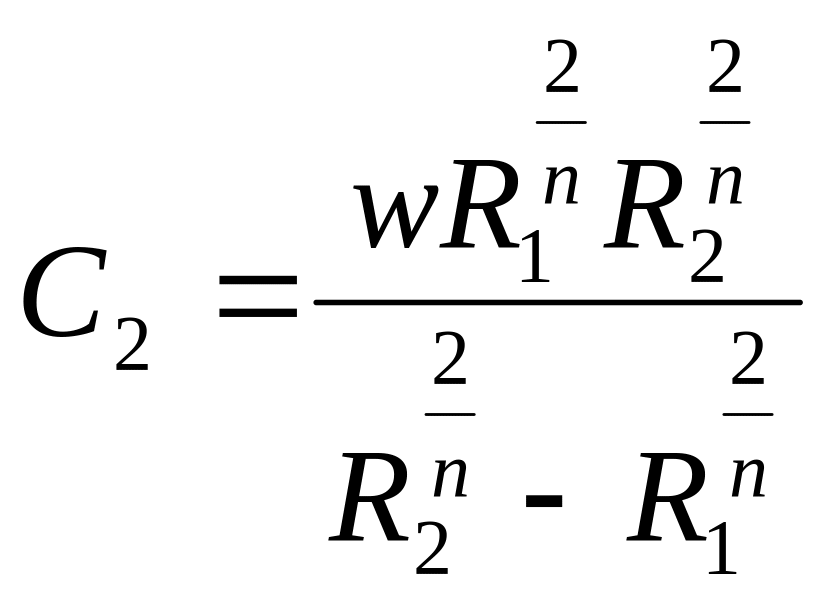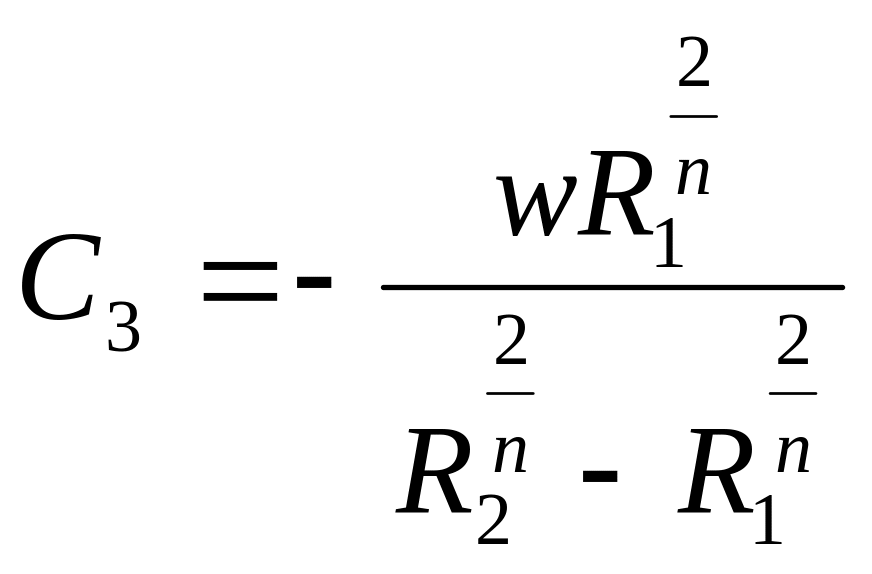
₍₂

Подставив вместо С₂ и С₃ их значения в уравнение (2.47), получаем уравнение профиля скорости:

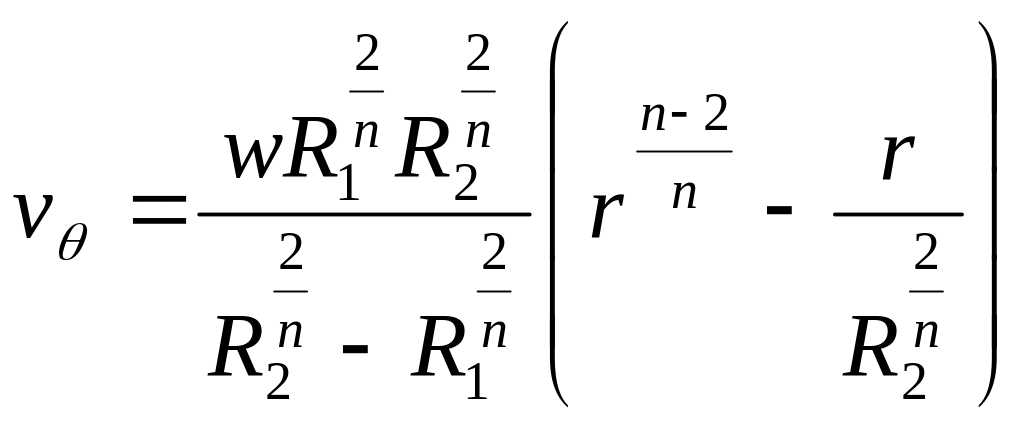
Для определения скорости сдвига воспользуемся уравнением (2.44) и равенством

Тогда скорость сдвига будет равна:

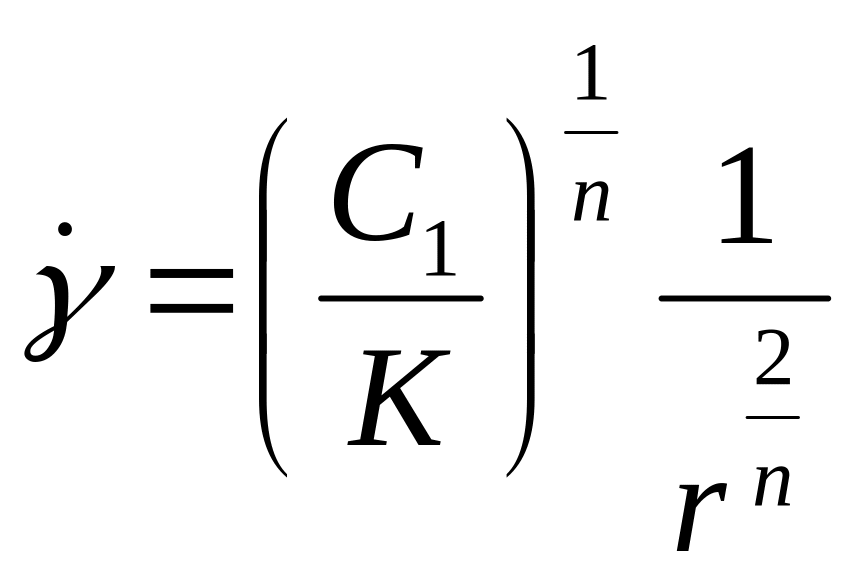
Подставив в это выражение значение из уравнения (2.46), а вместо С₂ из (2.48), имеем:

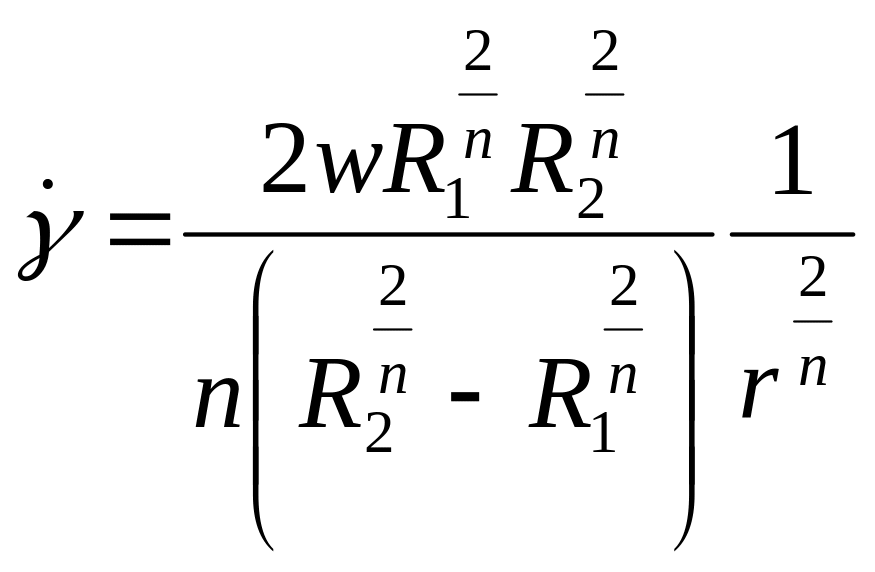
Скорость сдвига на внутреннем цилиндре определяем из уравнения (2.50) при r =R,

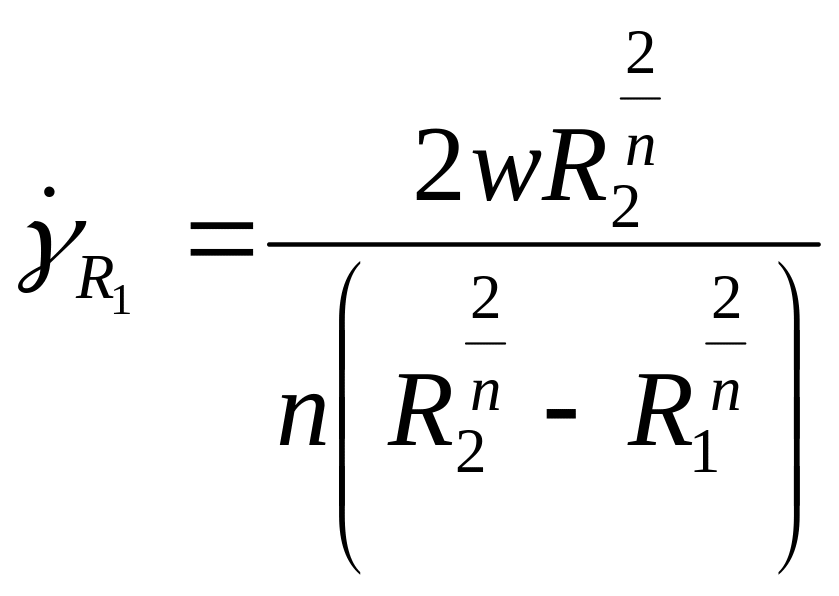
а на поверхности внешнего цилиндра при г = R₂:

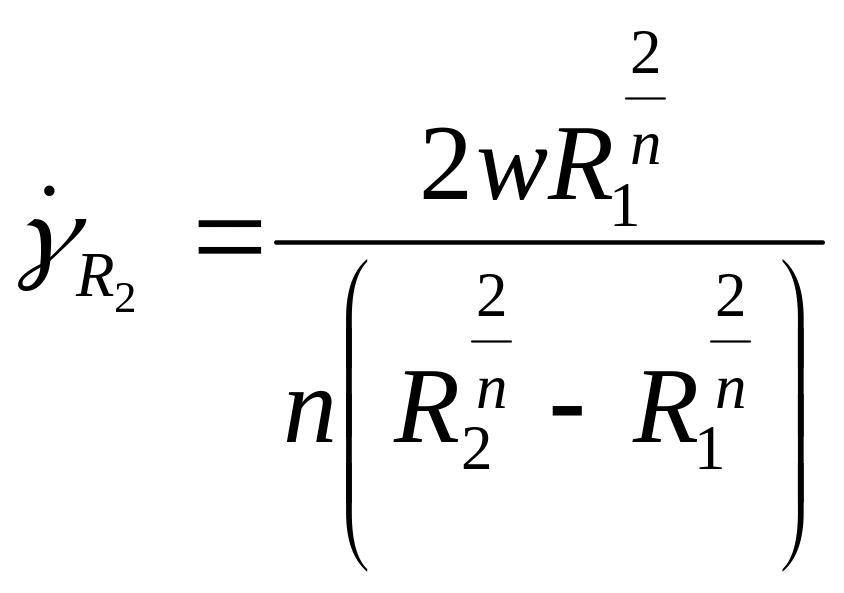
Напряжение сдвига на поверхности канала можно определить, используя равенство:

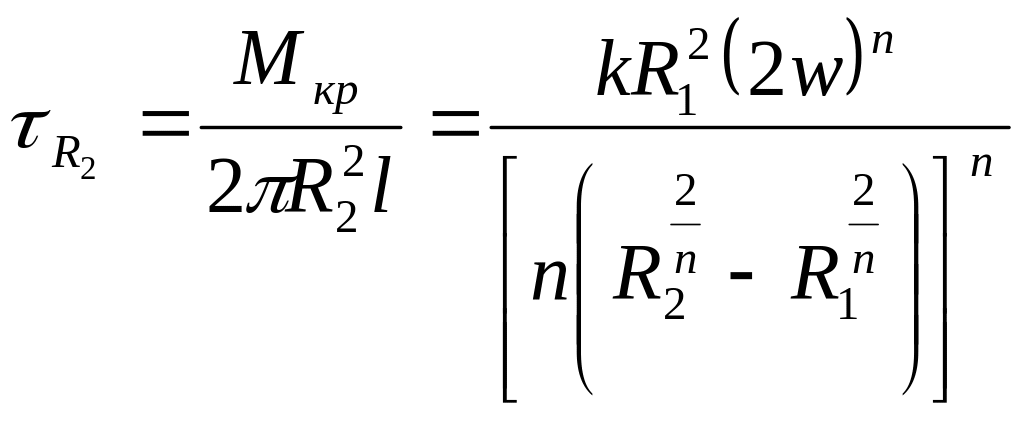
где М_кр - крутящий момент, возникающий при вращении цилиндра; l - длина цилиндра.

Полученные уравнения используются для обработки данных ротаци­онной вискозиметрии, а если при решении учесть наличие dp/dz = const, то для расчета формующих головок экструдеров, если мундштук или дорн вращаются. Подобные решения можно получить также для других случаев течения, принимая соответствующие граничные условия.

7. Изотермическое установившееся течение аномально вязких жидкостей между параллельными пластинами

Рассмотрим движение в щелевом канале, образованном двумя пластинами шириной В и длиной l, расстояние между которыми Н (рис. 2.15). Течение осуществляется вдоль оси z под действием перепада давления, при этом

Так как градиенты давлений по другим осям координат равны нулю, скорости, а соответственно и напряжения сдвига по ним будут также равны нулю:

Для решения принимаем допущения, приведенные в разделе 2.4. Уравнения движения в прямоугольных координатах имеют следующий вид.

Проанализировав уравнения движения с учетом принятых условий и допущений, получаем исходное выражение:

Так как течение установившееся и dp/dz = const, после интегрирования имеем:

Используя граничные условия, что в центре канала, при у = 0, вследствие симметрии потока (градиент скорости в центре канала равен нулю), имеем _yz= 0; тогда C₁ = 0. С учетом полученных значений получаем:

Напряжение сдвига на стенке канала, при у = Н/2 и перепаде

давления в канале, р = р₀ - р будет равно:

Реологическое степенное уравнение для движения между пластинами с учетом (2.13), (2.20) и (2.21) имеет вид:

Подставив вместо _yz его значение из (2.58), находим:

Проинтегрировав это выражение, получаем:

Постоянная интегрирования находится из условия, что скорость на поверхности канала при у = Н/2, v_z = 0, тогда:

Подставив вместо С₂ его значение, находим:

где v₀ - максимальная скорость потока,

Схема течения расплава между двумя неподвижными пластинами.

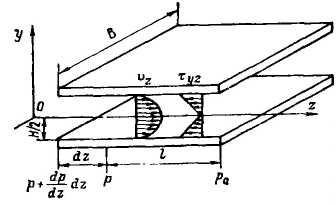
Рис. 2.13.

Для вывода уравнения расхода рас­плава выделим в поперечном сечении элемент толщиной dy и шириной В. Взяв произведение скорости xz на площадь этого элемента, равную произведению Bdy и проинтегрировав в пределах от 0 до Н/2, находим объемный расход расплава:

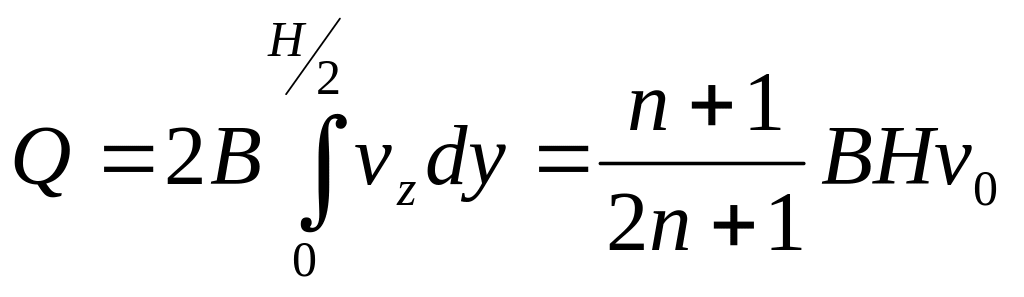
Уравнение скорости сдвига получаем, продифференцировав (2.60). Используя вместо v₀ его значение из уравнения (2.61), находим:

Скорость сдвига на поверхности пластины при у = Н/2, равна: