5. Изотермическое установившееся течение аномально вязких жидкостей в цилиндрическом канале

Рассмотрим течение расплава полимера под действием перепада давления вдоль оси канала с радиусом R и сравнительно большой дли­ной l. Давление на входе в канал равно р, а на выходе р₀. Так как течение установившееся, то принимаем, что , т.е. начальный входной участок канала, где не рассматривается. Перепады давлений по другим координатам равны нулю: . Соответственно скорости и напряжения сдвига также равны нулю , ,

Поскольку течение установившееся, то скорость вдоль оси z и во времени не изменяется, т.е.

,

Для решения принимаем следующие допущения:

1) вязкость расплава не изменяется во времени;

2) скольжение на стенках канала отсутствует, т.е. при r = R, v_z = 0;

3) нормальные напряжения при течении остаются постоянными, т.е.

, , ;

4) гравитационные силы не учитываем, так как канал расположен горизонтально: ;

5) инерционные силы равны нулю:

Схема течения расплава в цилиндрическом канале.

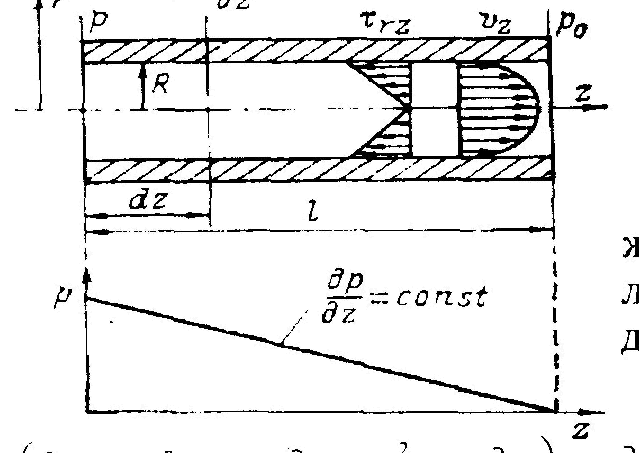
Рис. .

Рассмотрим произвольный элемент жидкости, расположенный внутри ци­линдрической поверхности, и запишем для него уравнение движения.

Проекция на направление r

Проекция на направление 

Проекция на направление z

Если проанализировать уравнения с учетом принятых условий и допущений, то видно, что все члены этих уравнений равны нулю, а из уравнения можем записать:

Для установившегося потока, когда градиент давления имеет постоян­ное значение,

полученное уравнение можно преобразовать в обычное дифференциаль­ное уравнение:

Интегрируя последнее выражение, находим:

На стенках канала скорость равна нулю, а в центре при r = 0 она максимальна. Следовательно, вследствие симметрии потока, на равных расстояниях от оси скорости также будут равны, поэтому скорость сдвига в центре канала отсутствует , поэтому _rz= 0.

Подставив в уравнение принятые граничные условия, находим, что`C₁= 0, тогда:

Макси­мальное значение напряжения будет на стенке канала при r =R и

равняется:

Знак минус указывает на то, что напряжения сдвига направлены в сторону, противоположную направлению оси z.

Для нахождения скорости потока воспользуемся реологическим уравнением (*), в которое вместо вязкости подставим степенное уравнение (**). С учетом принятых условий и допущений все члены уравнения (***), кроме , равны нулю. Поэтому в окончательном виде после подстановки этих значений в уравнение (*) имеем:

Подставив это значение _z в уравнение (****), из нового равенства находим:

Интегрируя это уравнение, получаем:

Из условия прилипания расплава к стенкам канала следует, что при r = R, v_z= 0, тогда:

Подставив вместо С₂ его значение, получаем:

Из уравнения (*****) при r = 0 можно определить максимальную скорость потока

Для вывода уравнения объемного расхода воспользуемся рис. *. Взяв в сечении канала элементарное кольцо с радиусом r и толщиной dr, находим его площадь: S = 2nrdr.

Сечение цилиндрического канала с выделенным элементарным кольцом толщиной dr.

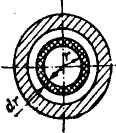
Рис.*.

Обычно расход расплава Q равен произведению площади сечения канала S на скорость потока v_z. Для полного сечения канала имеем:

Подставив вместо скорости v_z ее значение из уравнения (*******), получаем

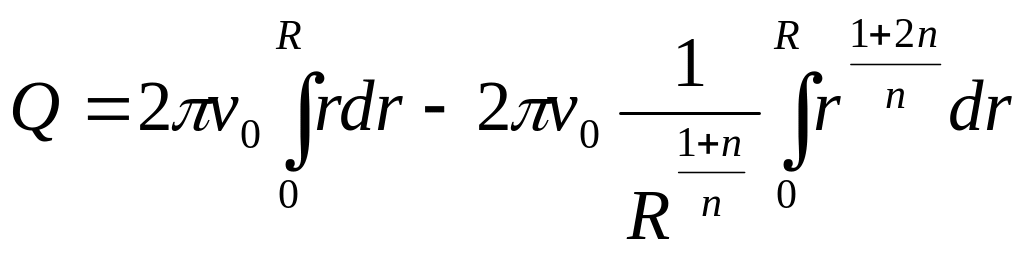
После интегрирования и преобразований получаем уравнение для расхода расплава

Для нахождения скорости сдвига продифференцируем уравнение

(*******)

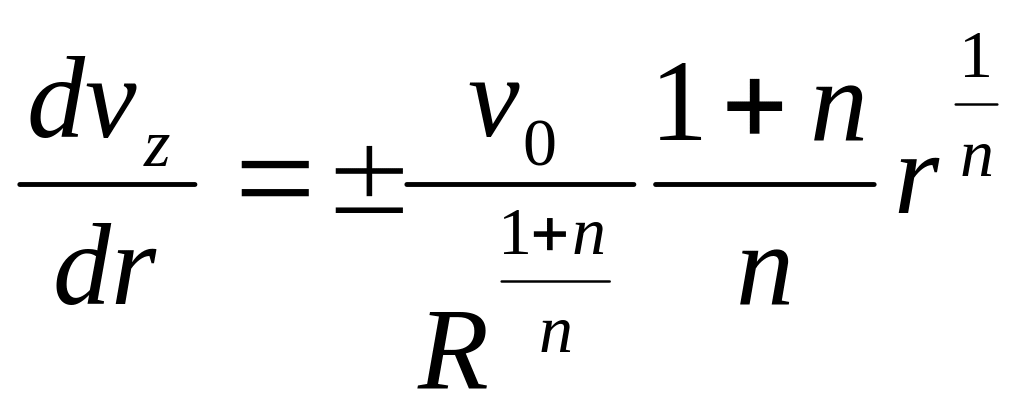
Заменив в этом уравнении v₀ его значением, найденным из уравнения (!!!!!) получаем:

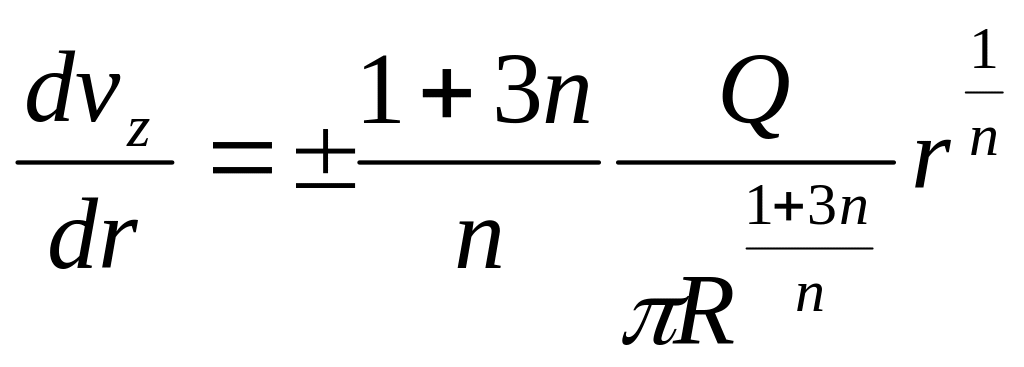
Скорость сдвига на стенке канала при r = R равна:

Полученные уравнения широко применяются при расчете экструзионных головок, литниковых каналов пресс-форм и в капиллярной вискозиметрии. Уравнение напряжения и скорости сдвига часто используют для определения степени ориентации макромолекул и последующего изменения свойств изделий. Построив эпюры напряжений и скорости сдвига, можно предсказать характер образования кристал­лических структур и изменение формы их по толщине экструзионного профиля или литьевого изделия в зависимости от степени ориентации макромолекул.

Если в уравнение (2.41) подставить n=1, то получаем скорость сдвига для потока ньютоновской жидкости: