
8.3. Явление самоиндукции и взаимной индукции
Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток сквозь проводящий контур. При этом совершенно не имеет значения, чем вызывается это изменение потока. Если по некоторому контуру течет изменяющийся во времени электрический ток, то магнитное поле этого тока также будет изменяться, а значит, будет изменяться магнитный поток через этот контур. Таким образом, изменение тока в контуре приводит к возникновению ЭДС индукции в этом же самом контуре. Это явление называется явлением самоиндукции, а возникающая при этом ЭДС – ЭДС самоиндукции.
В п. 6.7 было показано,
что магнитный поток через контур,
создаваемый током в контуре, Ф
= LI,
где L
– индуктивность контура. Строго говоря,
эта формула справедлива для постоянного
тока. Но ею можно пользоваться также и
в случае нестационарного тока, если он
изменяется так медленно, что время, в
течение которого ток претерпевает
существенное изменение, было велико по
сравнению с временем, которое требуется
электромагнитному процессу,
распространяющемуся со скоростью света,
пройти расстояние, равное длине контура,
т.е. при
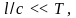 где l
– расстояние до самой удаленной точки
цеп T
– время изменения тока в цепи. Кроме
того, должно выполняться условие
где l
– расстояние до самой удаленной точки
цеп T
– время изменения тока в цепи. Кроме
того, должно выполняться условие
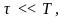 где
где
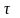 – время установления стационарного
движения зарядов в заданном квазистатическом
поле, т.е. время релаксации скорости
зарядов (см. п. 4.1). В этом случае мгновенное
значение тока будет практически одинаково
во всех поперечных сечениях электрической
цепи. Такой ток называется квазистационарным.
В дальнейшем предполагается, что условие
квазистационарности выполнено. Подставляя
эту формулу в формулу закона Фарадея,
получим
– время установления стационарного
движения зарядов в заданном квазистатическом
поле, т.е. время релаксации скорости
зарядов (см. п. 4.1). В этом случае мгновенное
значение тока будет практически одинаково
во всех поперечных сечениях электрической
цепи. Такой ток называется квазистационарным.
В дальнейшем предполагается, что условие
квазистационарности выполнено. Подставляя
эту формулу в формулу закона Фарадея,
получим

Если при изменении тока индуктивность L контура остается постоянной (не меняется геометрия контура и нет ферромагнетиков), то
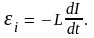
Знак минус показывает, что ЭДС самоиндукции всегда направлено так, чтобы препятствовать изменению силы тока – в соответствии с правилом Ленца. Эта ЭДС стремится сохранить ток неизменным: она противодействует протеканию току, когда он увеличивается, и поддерживает ток, когда он уменьшается.
В явлениях самоиндукции индуктивность L играет роль массы m, т.е. меры инертности электрической цепи по отношению к изменения тока а ней. Эффекты индукция стремятся сохранить электрический ток неизменным, точно так же, как механическая инерция стремится сохранить неизменной скорость тела. Характерные проявления самоиндукции наблюдаются при замыкании и размыкании цепи. Установление тока при замыкании и исчезновение его при размыкании происходит не мгновенно, а постепенно. Причем эти эффекты замедления тем значительнее, чем больше индуктивность цепи.
Представим себе теперь два проводящих неподвижных контура 1 и 2, находящихся на небольшом расстоянии друг от друга. И пусть в одном из них, например, в 1-ом ток I1 изменяется со временем. Тогда от времени будет зависеть и магнитное поле B1, создаваемое током I1, а следовательно, и магнитный поток, пронизывающий второй контур. Поэтому во втором контуре возникнет ЭДС индукции
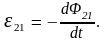
Эта ЭДС носит название ЭДС взаимной индукции, а само явление – явлением взаимной индукции. Учитывая, что Ф21 = L21I1, где L21 – взаимная индуктивность контуров, для ЭДС взаимной индукции получим
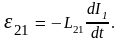
ЭДС взаимной индукции вызывает во втором контуре ток I2, который, как иток I1, так же будет нестационарным. Поэтому он в свою очередь, вызовет в первом контуре ЭДС взаимной индукции
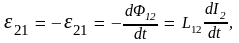
где
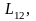 как и
как и
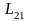 – взаимная индуктивность контуров.
Причем, как уже отмечалось,
=
– взаимная индуктивность контуров.
Причем, как уже отмечалось,
=
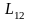 (при отсутствии ферромагнетиков).
(при отсутствии ферромагнетиков).
