Глава 7

МАГНИТИКИ В ПОСТОЯННОМ МАГНИТНОМ ПОЛЕ

7.1. Контур с током в магнитном поле

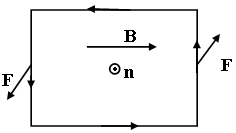
Поместим прямоугольный контур, по которому протекает ток, в однородное магнитное поле с индукцией B и рассмотрим три возможные ориентации контура по отношению к направлению вектора B (рис. 6.1). Построим нормаль n к контуру (единичный вектор, направленный перпендикулярно контуру так, что если смотреть навстречу ему, будем видеть направление течения тока против часовой стрелки).

В первом положении (рис. 6.1, а) нормаль n к контуру и вектор B направлены в одну сторону (угол между векторами n и B = = 0). Силы Ампера, действующие со стороны магнитного поля на каждую сторону рамки, направлены так, что они растягивают контур, не создавая вращающего контур момента. Во втором случае ( = π, рис. 6.1, б), силы Ампера сжимают контур. И лишь в третьем случае, когда = π/2, рис. 6.1, в), возникает пара сил, стремящаяся повернуть контур (против часовой стрелки). Момент этой пары M = Fb = I(ab)B = ISB, где b – длина большой стороны контура (плечо пары), S = ab – площадь контура.

а)

б)

в)

Рис. 6.1

В общем случае произвольного угла θ (рис. 6.2) вращающий момент создает нормальная к контуру составляющая B_n вектора

Рис. 6.2.

B. Ее модуль B_n = Bsinθ. Момент пары сил, созданной этой составляющей

M = ISB_n = ISBsinθ.

С учетом того, что n = = 1 представим это равенство в виде

В векторном виде это можно записать так

Учитывая, что ISn = p_m – магнитный момент контура (введенный в п. 3.6), будем иметь

Эта формула имеет такой же вид, как и формула (2.), определяющая вращающий момент, действующий на диполь в электрическом поле. С той лишь разницей, что вместо векторов и в формуле (6.) стоят векторы и .

_{Найдем работу по повороту контура с током в магнитном поле против направления действия момента силы (т.е. в сторону уменьшения угла θ):}

=

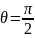
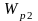Как видим, эта работа представляется в виде разности двух чисел и . Эти числа представляют собой значения потенциальной энергии контура в двух положениях 1 и 2. Таким образом, контур с током в магнитном поле обладает потенциальной энергией

где С – неопределенная постоянная. Для ее определения положение, при котором 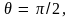примем за нулевое, т.е. будем считать, что Тогда получим C = 0. В результате будем иметь

(6.1)

Это равенство можно записать в векторной форме

Как видно из (6.1), потенциальная энергия контура достигает минимального значения, равного при и максимального значения, равного при В обоих этих положениях вращающий момент M равен нулю. Поэтому оба эти положения являются положениями равновесия контура. При этом первое положение является положением устойчивого равновесия контура, а второе – положением неустойчивого равновесия.