6.8. Работа по перемещению проводника с током в

магнитном поле

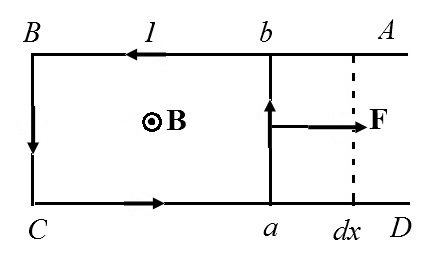
Рассмотрим П-образный проводник АВСD, вдоль которого может перемещаться перемычка аb (рис. 5). Проводник находится в однородном магнитном поле с индукцией B. По проводнику проте-

Рис. 5.

кает ток I. При указанных на рисунке направлениях тока I и индукции B на перемычку ab будет действовать сила Ампера F = IBl, где l – длина перемычки ab. Эта сила будет заставлять перемещаться перемычку слева направо вдоль проводника ABCD. Работа, совершаемая этой силой на перемещении dx будет равна

δA = Fdx = IBldx = IBdS = IdФ. (5.24)

Здесь dS = ldx – площадь, заметаемая перемычкой ab при перемещении ее на расстояние dx, dФ = BdS – приращение потока, пронизывающего контур abBC, при указанном перемещении перемычки. При конечном перемещении работа определится интегрированием выражения (5.21). В результате придем к выражению

(5.25)

Формула (5.22) может применяться также и для вычисления работы, которая совершается в магнитном поле при перемещениях замкнутых контуров. Для замкнутых контуров ∆Ф означает изменение магнитного потока через площадь, охваченную этим контуром. Таким образом, работа сил магнитного поля при перемещении контура с током равна произведению силы тока на приращение магнитного потока, пронизывающего этот контур.

Формулу (5.22) можно обобщить и на случай любого изменения магнитного потока. В частности, она справедлива и в том случае, если в неподвижном контуре изменяется сила тока.

6.9. Основные уравнения стационарного магнитного поля в вакууме

Магнитное поле создается движущимися электрическими зарядами. Магнитных зарядов как источников магнитного поля, аналогичных электрическим зарядам источников электрического поля, в природе не существует. Магнитное поле не имеет источников и стоков. Если бы магнитные заряды существовали, то, как это имеет место в случае электрических зарядов и электрических силовых линий, магнитные силовые линии начинались бы на магнитных зарядах одного знака и заканчивались на зарядах другого знака либо уходили на бесконечность. Но поскольку магнитных зарядов нет, то силовые линии магнитного поля не имеют ни начала, ни конца, они замкнуты. Поэтому если в магнитном поле построить произвольную замкнутую поверхность S, то число магнитных силовых линий, входящих в объем, ограниченный этой поверхностью, будет равно числу линий, выходящих из этого объема. Следовательно, поток вектора индукции магнитного поля (магнитный поток) через любую замкнутую поверхность S равен нулю:

(6.14)

В СИ магнитный поток измеряется в веберах: 1 Вб = 1 Тл∙м². Соотношение (5.11), представляющее собой теорему Гаусса для вектора индукции магнитного поля B. Его называют первым основным уравнением (или первым уравнением Максвелла) для стационарного магнитного поля в вакууме. Оно является математическим выражением экспериментально установленного факта отсутствия в природе магнитных зарядов (во всяком случае, в свободном виде).

Используя математическую теорему Остроградского – Гаусса, уравнение (3.11) можно записать в дифференциальной форме:

(6.15)

Найдем теперь циркуляцию вектора индукции магнитного поля, т.е. вычислим интеграл по замкнутому контуру L. Рассмотрим случай прямого бесконечно длинного проводника с током. Предположим, что контур, охватывающий прямой ток, лежит в плоскости, перпендикулярной току, и представляет собой окружность радиусом r с центром на проводнике. Поскольку эта окружность совпадает с одной из линий вектора B, то векторы B и dl в каждой точке будут сонаправлены, и тогда

При вычислении этого интеграла была использована формула (3.5) и учтено, что dl от радиуса окружности r не зависит. Следовательно, в случае магнитного поля, создаваемого прямым бесконечно длинным проводником с током

(6.16)

Оказывается, что контур L не обязательно должен совпадать с силовой линией: он может быть произвольным, лишь бы он охватывал ток I. Более того, могут быть произвольными и форма и размер проводника, а контур L может охватывать много проводников, по которым текут токи I₁, I₂, I₃, …, и тогда под I в формуле (5.13) следует понимать алгебраическую сумму токов, охватываемых контуром L: При этом токи считаются положительными, если их направления связаны с направлением обхода контура правилом правого буравчика и отрицательными – если они текут в обратном направлении.

Таким образом, для магнитного поля, создаваемого любым проводником с током, циркуляция вектора индукции магнитного поля вдоль произвольного контура равна умноженной на алгебраической сумме сил токов, пронизывающих этот контур. Это соотношение носит название закона полного тока и представляет собой второе основное уравнение (или второе уравнение Максвелла) для стационарного магнитного поля в вакууме.

Поскольку циркуляция вектора индукции магнитного поля отлична от нуля, магнитное поле является вихревым. Лини вектора такого поля замкнуты.

Используя формулу (2.3), связывающую силу тока с плотностью тока, и математическую теорему Стокса, уравнение (3.13) можно записать в дифференциальной форме:

(6.17)

Уравнения (3.12) и (3.14) полностью определяют магнитное поле, порожденное любым постоянным током.

Так как магнитное поле не является потенциальным, вектор нельзя представить в виде градиента некоторой скалярной функции. Это означает, что для магнитного понятие скалярного потенциала, аналогичного потенциалу электростатического поля, ввести нельзя. Однако так как дивергенция ротора любого вектора равна нулю, то общим решением уравнения (3.12) является вектор

. (6.18)

Вектор называется векторным потенциалом (или вектор-потенциалом) магнитного поля. В магнитостатике он играет примерно такую же роль, как и скалярный потенциал в электростатике. Если наложить на него условие то этот потенциал будет удовлетворять уравнению

аналогичному уравнению Пуассона для потенциала электрического поля. Из аналогии следует, что A определяется такой же функцией, как и , но с заменой на . А поскольку плотность заряда а плотность тока то выражение для вектор-потенциала A можно получить, заменив в формуле для электрического потенциала коэффициент на Таким путем найдем, например, вектор-потенциал движущегося точечного заряда:

Взяв ротор этого вектора, придем к ранее полученной формуле для вектора индукции магнитного поля, создаваемого равномерно движущимся точечным зарядом:

(6.19)

Как видно из этой формулы, вектор B направлен перпендикулярно векторам v и e_r и образуют с этими векторами правовинтовую систему. Силовые линии вектора B представляют собой систему коаксиальных окружностей (рис.3.). Направление вектора B можно определить, пользуясь «правилом правой руки»: если мысленно взять ладонью правой руки вектор v, направив большой палец вдоль этого вектора, то четыре оставшихся пальца покажут направление линий вектора B.