6.6.2. Магнитное поле кругового тока

Используем закон Био – Савара – Лапласа для определения магнитного поля постоянного тока I, текущего по проводу в форме окружности радиуса R. Найдем индукцию магнитного поля на рас-

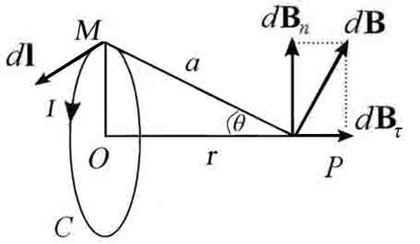
стоянии r от центра кругового тока. На рис. 5.5 изображен вектор dl, характеризующий малый элемент длины проводника с током, и вектор a, направленный от элемента dl к точке наблюдения Р. По определению векторного произведения из формулы (5.20) следует, что вектор dB магнитной индукции поля, создаваемого рассматриваемым элементом тока, перпендикулярен и вектору dl, и вектору

а. Таким образом, начало вектора dB находится в точке Р, а сам вектор направлен как показано на рис. 5.5.

Так как векторы dl, и a образуют прямой угол, для модуля вектора dB будем иметь

(6.23)

Разложим вектор dB на две составляющие: составляющую – перпендикулярную оси симметрии кольца, и составляющую 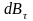– совпадающую с осью симметрии кольца. Из рис. 5.5. видно, что

Рис. 6.

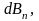составляющие от диаметрально противоположно расположенных элементов dl, будут взаимно компенсироваться, т.е. при интегрировании по всему кольцу эта компонента исчезнет. И, наоборот, компоненты будут складываться. Поэтому далее мы будем рассматривать только направленную вдоль оси симметрии компоненту поля. Из рис. 5.5. видно также, что Поэтому для индукции магнитного поля, создаваемого, элементом контура dl вдоль оси симметрии, получается следующее выражение:

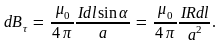
Для определения результирующего поля это выражение следует проинтегрировать по всему контуру:

Введем в рассмотрение вектор и назовем его магнитным моментом контура. Этот вектор по модулю равен площади контура, а его направление совпадает с направлением нормали к контуру. Используя это понятие и учитывая, что для кругового витка S = πR² выражение (5.22) можно записать так:

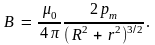(5.23)

Отметим, что направление вектора магнитной индукции круго-

Рис. 6.

вого тока, как и вектора магнитного момента, связано с направлением тока правилом правого винта.

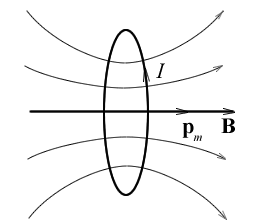
Линии вектора в пространстве имеют вид, показанный на рис. 5.6.

В центре кругового витка индукция магнитного поля будет

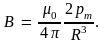
На очень большом расстоянии от центра (r << R) индукция магнитного поля

При этом во всех случаях вектор магнитной игндукции направлен так же, как и магнитный момент кольца (как показано на рис. 5.6).

6.7. Действие магнитного поля на проводник током. Закон Ампера

Предположим, что в однородном магнитном поле с индукцией B находится проводник произвольной формы, по которому протекает ток I. Найдем силу, действующую на этот проводник со стороны магнитного поля. Эту силу называют силой Ампера. Разобьем

Рис. 6

проводник на отдельные бесконечно малые элементы и рассмотрим элемент длины про-

водника dl (рис. 5.7). На каждый свободный электрон, движущийся через этот элемент, действует сила Лоренца, 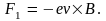В отсутствие тока электроны движутся хаотически,

поэтому все эти силы тоже направлены хаотически, и результирующая сила, действующая на указанный элемент, равна нулю. При наличии тока, все электроны движутся в одном направлении, в одном направлении будут действовать и силы, и, векторно складываясь, образуют результирующую силу, действующую на элемент dl. Поскольку элемент dl мал, силы, действующие на электроны, равны по величине и одинаковы по направлению. Поэтому результирующую силу, действующую на выделенный элемент, можно найти, умножив силу F₁ на число электронов dN = nSdl в этом элементе. Следовательно,

dF = F₁dN = ev B = Idl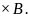

Эту формулу называют формулой силы Ампера. Направление силы Ампера можно определить по правилу левой руки: расположим ладонь левой руки так, чтобы линии вектора В входили в нее, а четыре вытянутых пальца направить вдоль направления силы тока, тогда отведенный в сторону большой палец покажет направление силы Ампера.

Силу, действующую на весь проводник, можно найти, проинтегрировав это выражение по длине проводника.

Вернемся теперь к двум параллельным прямым бесконечно длинным проводникам с током Учитывая направление сил взаимодействия проводников, формулу закона Ампера можно записать в скалярном виде 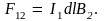Будем считать, что ток I₁ находится в магнитном поле B₂, созданном вторым током I₂. Тогда эту формулу можно рассматривать как силу действующую на проводник 1 со стороны поля, созданного проводником 2. 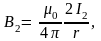Подставив в нее значение придем к формуле (6.2).