- •Часть II. Магнетизм
- •Глава 6.
- •6.1. Магнитное поле. Вектор индукции магнитного поля
- •6.2. Магнетизм как релятивистский эффект
- •6.5. Магнитное поле тока.
- •6.6.2. Магнитное поле кругового тока
- •6.7. Действие магнитного поля на проводник током. Закон Ампера
- •6.8. Работа по перемещению проводника с током в
- •6.9. Основные уравнения стационарного магнитного поля в вакууме
- •6.10. Применение закона полного тока к расчету
- •6.10.1. Магнитное поле соленоида
- •6.10.2. Магнитное поле тороида
- •6.11. Движение заряженных частиц в магнитных полях
- •6.11.1. Особенности движения заряженной частицы в
- •6.11.2. Эффект Холла
6.5. Магнитное поле тока.
Закон Био – Савара – Лапласа
Как уже отмечалось, всякая движущаяся заряженная частица, кроме электрического, создает также и магнитное поле. Электрические поля металлических проводников, созданные отрицательными свободными электронами и положительными ионами, компенсируют друг друга. Что касается магнитных полей, созданных хаотически движущимися свободными электронами, они также компенсируют друг друга вследствие хаотического направления их в пространстве. Если же по проводнику протекает ток, т.е. если электро-
Рис. 6. |
нитные поля также будут направлены в одну сторону, и, складываясь друг с другом, будут создавать результирующее поле проводника с током.
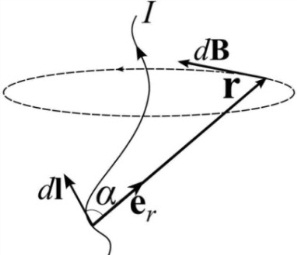
Пусть имеем проводник произвольной формы, по которому протекает ток I (рис. 5.4). Найдем индукцию магнитного поля этого проводника. Разобьем мысленно этот проводник на отдельные бесконечно малые элементы dl. Так как этот элемент мал, то проходящие через него электроны создают в произвольной точке Р одинаковые по величине и по направлению магнитные поля. Поэтому магнитное поле, созданное этим элементом можно найти, умножив индукцию поля, созданного одним электроном
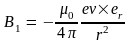 (6.20)
(6.20)
На
число электронов dN
= nSdl,
находящихся в указанном элементе dl,
где S
– площадь поперечного сечения проводника,
n
– число свободных электронов в единице
объема проводника (концентрация свободных
электронов в проводнике). Учитывая, что так как векторы v
и dl
направлены противоположно, получим
так как векторы v
и dl
направлены противоположно, получим
 (6.21)
(6.21)
где
 –
единичный вектор, направленный от центра
элемента длины dl
проводника к точке наблюдения Р
(вдоль вектора r).
Величину Idl
называют элементом тока проводника. В
скалярной форме
–
единичный вектор, направленный от центра
элемента длины dl
проводника к точке наблюдения Р
(вдоль вектора r).
Величину Idl
называют элементом тока проводника. В
скалярной форме
 (6.22)
(6.22)
где
 – угол между векторами dl
и r.
– угол между векторами dl
и r.
Формула (5.20) определяет индукцию магнитного поля, созданного элементом тока проводника и носит название закона Био – Савара – Лапласа.
Индукцию магнитного поля, созданного всем проводником, можно найти, просуммировав поля от каждого элемента, т.е. проинтегрировав выражение (5.20) по длине проводника.
Заметим, что индукция магнитного поля, созданного любым проводником, пропорциональна току, текущему по проводнику.
6.5. Применение закона Био – Савара – Лапласа
к расчету магнитных полей
6.5.1. Магнитное поле прямого тока
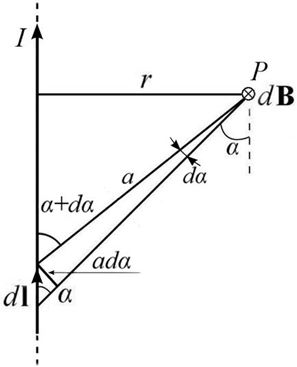
В качестве первого примера применения закона Био – Савара – Лапласа получим выражение для индукции магнитного поля, созданного бесконечно длинным прямым проводником с током (пря-
Рис. 6. |
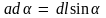 ,
откуда dl = adα
/ sinα.
Тогда dl = adα
/sin2α.
С учетом этого формулу закона Био –
Савара – Лапласа
,
откуда dl = adα
/ sinα.
Тогда dl = adα
/sin2α.
С учетом этого формулу закона Био –
Савара – Лапласа

приводим к виду

При интегрировании этого равенства по углу α учтем, что когда элемент dl будет находиться «бесконечно далеко» внизу, угол α будет стремиться к нулю, так что нижний предел интегрирования равен нулю. Аналогично, когда элемент тока dl будет находиться «бесконечно далеко» вверху, угол α будет стремиться к 1800, а верхний предел будет равен π. Таким образом, индукция магнитного поля в точке наблюдения Р найдется как

Таким образом, Индукция магнитного поля, созданного прямым бесконечно длинным проводником с током определяется только током, текущим по проводнику и расстоянием до точки наблюдения: