Часть II. Магнетизм

Глава 6.

СТАЦИОНАРНОЕ МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

6.1. Магнитное поле. Вектор индукции магнитного поля

Из опыта известно, что электрические токи взаимодействуют между собой, а также токи и движущиеся электрические заряды. Так, два параллельных проводника с током притягиваются друг к другу, если токи в них имеют одинаковые направления, и отталкиваются, если токи противоположны. Как показал Ампер, сила взаимодействия, приходящаяся на единицу длины, двух очень длинных (бесконечно длинных) параллельных проводников с токами I₁ и I₂ пропорциональна произведению сил токов I₁ и I₂ и обратно пропорциональна расстоянию r между проводниками:

(6.1)

Причем эти силы являются силами притяжения, если токи текут в одном направлении и силами отталкивания, – если в противоположном.

Коэффициент пропорциональности в (5.1) – некоторая постоянная, аналогичная постоянной 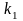в законе Кулона, зависящая от выбора системы единиц (множитель 2 выбран для удобства). В системе СИ сила тока измеряется в амперах. По определению сила тока в 1А – это такая сила тока, который, протекая по двум очень длинным параллельным проводам, расположенным на расстоянии 1м друг от друга, создают силу взаимодействия, приходящуюся на каждый метр длины проводов, равную Подставляя это в формулу (3.1) при I₁ = I₂ = 1А и r = 1м, найдем постоянную : Учитывая, что в системе СИ постоянная и 1Кл = 1А∙с, представим постоянную в виде

где – так называемая магнитная постоянная (Гн – единица индуктивности генри). Тогда формула Ампера в системе СИ запишется в виде

(6.2)

Анализ взаимодействия проводников с током друг с другом и с движущимися электрическими зарядами приводит к выводу, что при движении зарядов помимо электрических сил возникают дополнительные силы взаимодействия. Эти силы называют магнитными силами. Действительно, металлический проводник представляет собой электрически нейтральную систему зарядов (положительных ионов в узлах решетки и отрицательных свободных электронов, хаотически движущихся между узлами). Электронейтральность (баланс положительных и отрицательных зарядов) не нарушится, если электроны в проводнике привести в упорядоченное движение. Поэтому взаимодействие проводников с током нельзя объяснить электрическими силами. Остается предположить, что при движении зарядов возникают дополнительные силы взаимодействия. Если токи в проводниках отсутствуют, то вследствие хаотичности движения электронов магнитные силы взаимодействия между движущимися электронами двух проводников также направлены хаотически и, векторно складываясь, компенсируют друг друга – взаимодействие проводников отсутствует. При упорядоченном же движении электронов в проводниках магнитные силы взаимодействия электронов двух проводников будут направлены одинаково и, складываясь векторно между собой, создают результирующую силу взаимодействия.

Аналогично можно объяснить и взаимодействие проводника с током с движущимся параллельно проводнику электрическим зарядом.

Аналогично тому, как для описания электрического взаимодействия вводится понятие электрическое поля, для описания магнитного взаимодействия можно ввести понятие магнитного поля. Именно, можно считать, что магнитное взаимодействие движущихся с постоянной скоростью электрических зарядов или системы движущихся зарядов – постоянных токов осуществляется посредством постоянного магнитного поля. Движущиеся электрические заряды (токи) изменяют свойства окружающего пространства – создают в нем магнитное поле. Это поле проявляется в том, что действует на движущиеся в нем электрические заряды (токи).

Таким образом, согласно полевой концепции взаимодействие движущихся электрических зарядов (электрических токов) объясняется тем, что каждый движущийся заряд (ток) изменяет свойства окружающего пространства – создает в нем магнитное поле, которое проявляется в том, что действует на другой движущийся заряд (ток).

Мы видим, что магнитное поле, как и поле электрическое, связано с электрическим зарядом двояким образом: с одной стороны, магнитное поле порождается электрическим зарядом, а с другой – оно воздействует на электрический заряд. Однако если электрическое поле создается электрическим зарядом всегда, независимо от того, покоится или движется заряд, то магнитное поле создается только движущимся зарядом. Если электрическое поле воздействует на электрический заряд всегда, независимо от того, покоится или движется заряд, то магнитное поле действует только на движущийся заряд.

Опыт показывает, что сила F, действующая на точечный заряд q, движущийся в магнитном поле со скоростью v, пропорциональна величине заряда, скорости его движения и направлена перпендикулярно этой скорости и некоторому выделенному направлению в пространстве. Математически это можно записать в виде векторного произведения

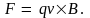(6.3)

Вектор B характеризует магнитное поле и определяет указанное направление в пространстве. Этот вектор называется вектором индукции магнитного поля. Сила, определяемая формулой (3.3), называется силой Лоренца. По известному направлению вектора B направление силы, действующей на положительный заряд можно определить по правилу левой руки: если левую руку расположить так, чтобы линии вектора B входили в ладонь, четыре вытянутые пальца направить вдоль скорости заряда, то отставленный в сторону большой палец покажет направление силы F.

Формулу (3.3) можно использовать в качестве исходной формулы для определения величины и направления вектора магнитной индукции B. Будем перемещать заряд в магнитном поле. Изменяя направление движения, найдем такое направление, в котором магнитная сила равна нулю. Так как векторное произведение коллинеарных векторов равно нулю, то полученное направление и есть направление вектора B. Выберем теперь направление скорости, перпендикулярно направлению вектора B. В этом случае формулу (3.3) можно записать в скалярном виде откуда

(6.4)

Таким образом, индукция магнитного поля в некоторой точке численно равна силе, действующей на единичный положительный заряд, имеющий единичную скорость, перпендикулярную вектору B в данной точке. Видим, что индукция магнитного поля является силовой характеристикой магнитного поля, подобно тому, как вектор E является силовой характеристикой электрического поля.

Размерность индукции магнитного поля получим, используя формулу (3.4):

Эту единицу измерения называют тесла.

Поскольку вектор B является силовой характеристикой магнитного поля, линии этого вектора называют магнитными силовыми линиями (или силовыми линиями магнитного поля).

Так же, как и для поля электрического, для магнитного поля справедлив принцип суперпозиции. В данном случае этот принцип формулируется так: магнитное поле B, создаваемое совокупностью источников, равна векторной сумме магнитных индукций B₁, B₂, B₃, … ,B_n, создаваемых каждым из источников в отдельности:

В электростатике чтобы получить силу F_e, действующую на заряд, следует этот заряд q умножить на напряженность поля E в точке расположения заряда: F_e = qE. Чтобы получить силу Лоренца, действующую со стороны магнитного поля на движущийся заряд, мы векторно умножаем вектор qv на вектор индукции B магнитного поля, в котором движется заряд: Применяя этот прием получим формулу индукции магнитного поля В, создаваемого равномерно движущимся точечного зарядом q, Будем исходить из формулы напряженности электрического поля неподвижного заряда где e_r – единичный вектор, направленный вдоль вектора r. Заменим в этой формуле q на вектор qv, а операцию обычного умножения – на векторную. Чтобы теперь согласовать размерности полученного выражения и индукции В, следует это выражение разделить на квадрат какой-то скорости. Скорость движения заряда уже использована, и остается единственная возможность – фундаментальная физическая постоянная, скорость света с:

Учтя, что , придем к формуле

(6.6)

В скалярной форме эта формула будет иметь вид

где α – угол между вектором скорости и направлением на точку наблюдения.