10.3. Формулы Френеля

10.3.1. Вывод формул Френеля

Граничные условия позволяют не только определить направления распространения отраженной и преломленной волн, но и выразить их амплитуды через амплитуду падающей волны. С учетом равенства фазовых множителей exp[i (k×r – w t)] трех волн на границе раздела сред граничные условия можно записать в виде

(14.5)

При этом амплитуды полей и в электромагнитной волне в веществе связаны соотношением вида

(14.6)

Значения проекций амплитуд и т.д., очевидно, зависят

Рис. 9.

от ориентации векторов E и B (ориентация вектора B однозначно определяется ориентацией вектора E) волн относительно плоскости падения. Так как вектор E каждой волны можно разложить на две составляющие, одна из которых лежит в плоскости падения, а другая перпендикулярно ей, то достаточно рассмотреть эти две взаимно перпендикулярные

Рис. 9.

ориентации вектора E или, иначе говоря, две взаимно перпендикулярные линейные поляризации волн. Будем обозначать их индексами || и ^. (Параллельную и перпендикулярную поляризации часто называют соответственно p- и s-поляризациями.) Положительными направлениями векторов E и B будем считать такие, при которых эти векторы образуют с вектором k правую тройку.

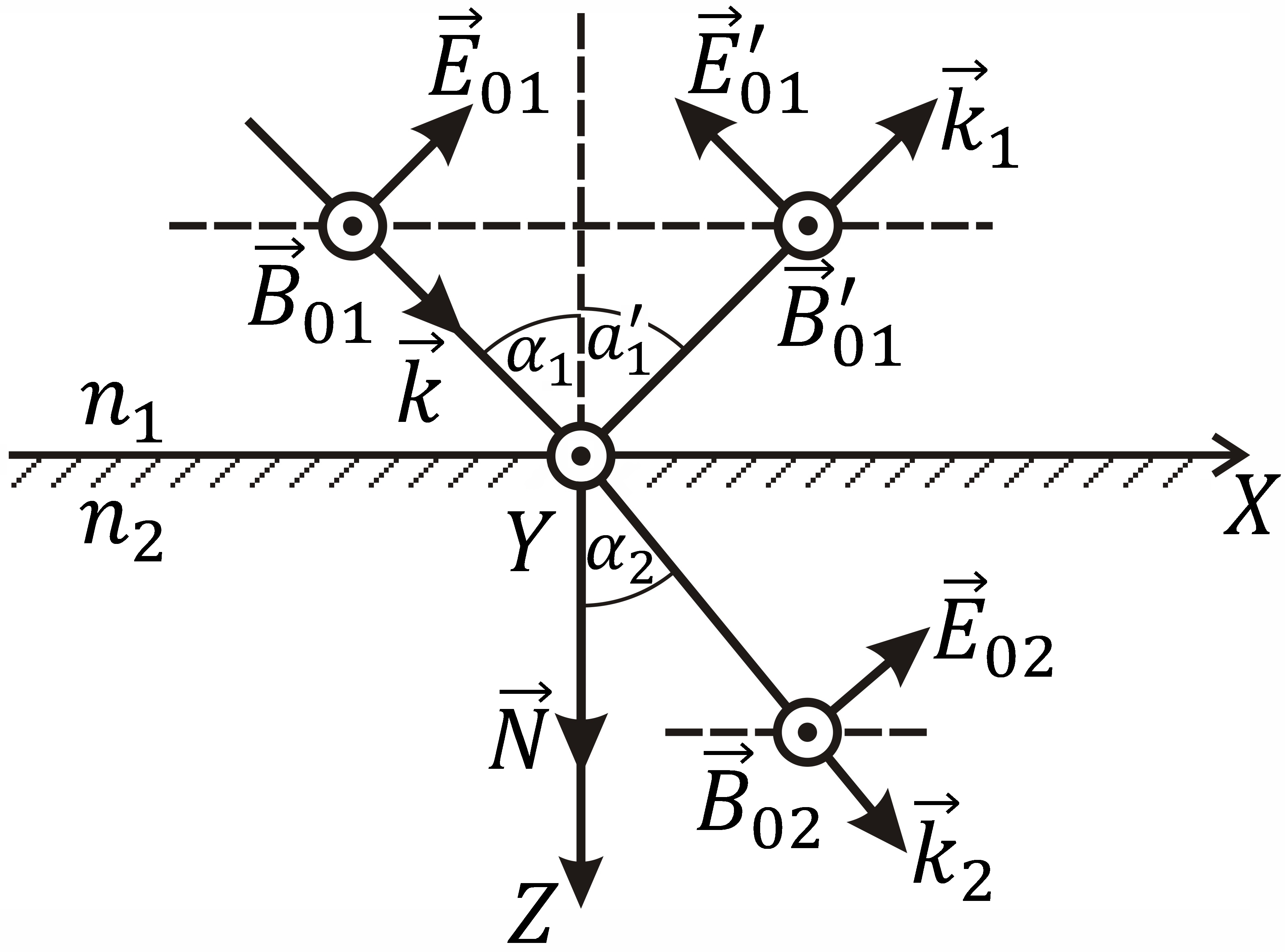
Случай параллельной поляризации показан на рис. 14.2, а. В этом случае поэтому равенства (14.5) с учетом, что принимают вид

(14.7)

(14.8)

Выразив в равенстве (14.8) амплитуду поля B через амплитуду поля E по формуле (14.6), преобразуем его к виду

(14.9)

Решая систему уравнений (14.7) и (14.9) относительно и выразим амплитуды отраженной и преломленной волн через амплитуду падающей волны в случае, когда векторы E лежат в плоскости падения:

(E¢₀₁) _|| = (E₀₁) _||, (E₀₂)_|| = (E₀₁) _||. (14.10)

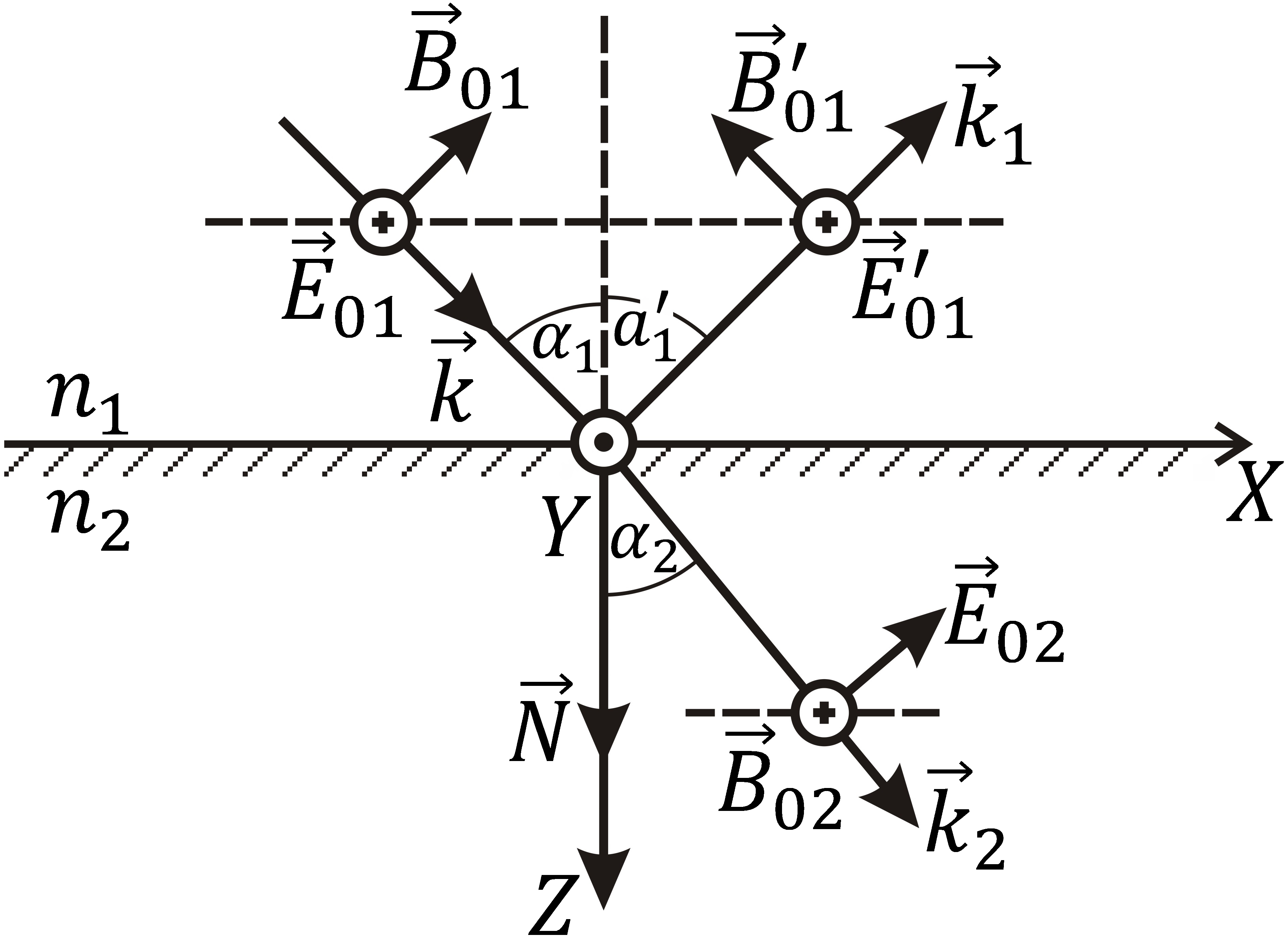
Случай перпендикулярной поляризации показан на рис. 14.2, б. Теперь поэтому равенства (14.5) с учетом, что принимают вид

С учетом соотношения (14.6) эти равенства перепишем в виде

Решив эту систему, выразим амплитуды отраженной и преломленной волн и через амплитуду падающей волны в случае, когда векторы E перпендикулярны плоскости падения:

(E¢₀₁)_^ = (E₀₁)_^, (E₀₂)_^ = (E₀₁)_^. (14.11)

Соотношения (14.10) и (14.11) называют формулами Френеля. Исключив из этих равенств отношение с помощью закона преломления, приведем формулы Френеля к виду

(E¢₀₁) _|| = (E₀₁) _||, (E₀₂) _|| = (E₀₁) _|| (14.12)

при поляризации, параллельной плоскости падения;

(E¢₀₁)_^ = (E₀₁)_^, (E₀₂)_^ = (E₀₁)_^. (14.13)

при поляризации, перпендикулярной плоскости падения.

Формулы Френеля полностью определяют амплитуды и фазы отраженной и преломленной волн, если известны амплитуда и фаза падающей волны (напомним, что амплитуды E₀₁, E¢₀₁, E₀₂ – комплексные величины, поэтому они включают в себя фазовые множители вида exp(-ij)).