Глава 10

СВЕТОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА СРЕД

10.1. Законы отражения и преломления света

Предположим, что имеются две прозрачные однородные и изотропные среды 1 и 2, разделенные плоской поверхностью и характеризуемые показателями преломления и . На границу раздела сред из среды 1 под углом к нормали N к границе падает плоская монохроматическая волна E₁ = E₁₀ exp [i (k₁×r – w₁t)]. Опыт показывает, что при этом от границы раздела будут распро-

страняться две плоские волны: одна в среде 1 (отраженная волна), другая в среде 2 (преломленная волна). Запишем эти волны соответственно в виде

E¢₁ = E¢₀₁ exp [i (k¢₁×r – w¢₁t)], E₂ = E₀₂ exp [i (k₂×r – w₂t)]. Направления распространения всех трех волн, определяемых вол-

Рис. 9.1

новыми векторами k₁, k¢₁ и k₂, показаны на рис. 9.1. Плоскость, в которой лежат векторы k₁ и N, называется плоскостью падения. Углы , и которые образуют векторы k₁, k¢₁ и k₂ с вектором нормали N, называются соответственно углами падения, отражения и преломления.

Связь между указанными тремя волнами определяется граничными условиями векторов E и B. Эти условия вытекают из уравнений Максвелла и заключаются в том, что тангенциальные составляющие векторов E и B непрерывны на границе раздела сред:

E_t⁽¹⁾ = E_t⁽²⁾, B_t⁽¹⁾ = B_t⁽²⁾,

где индексы 1 и 2 обозначают обе среды, а t – тангенциальные компоненты полей. Существенно, что этим граничным условиям будут удовлетворяться, если рассматривать именно три волны: падающую, отраженную и преломленную.

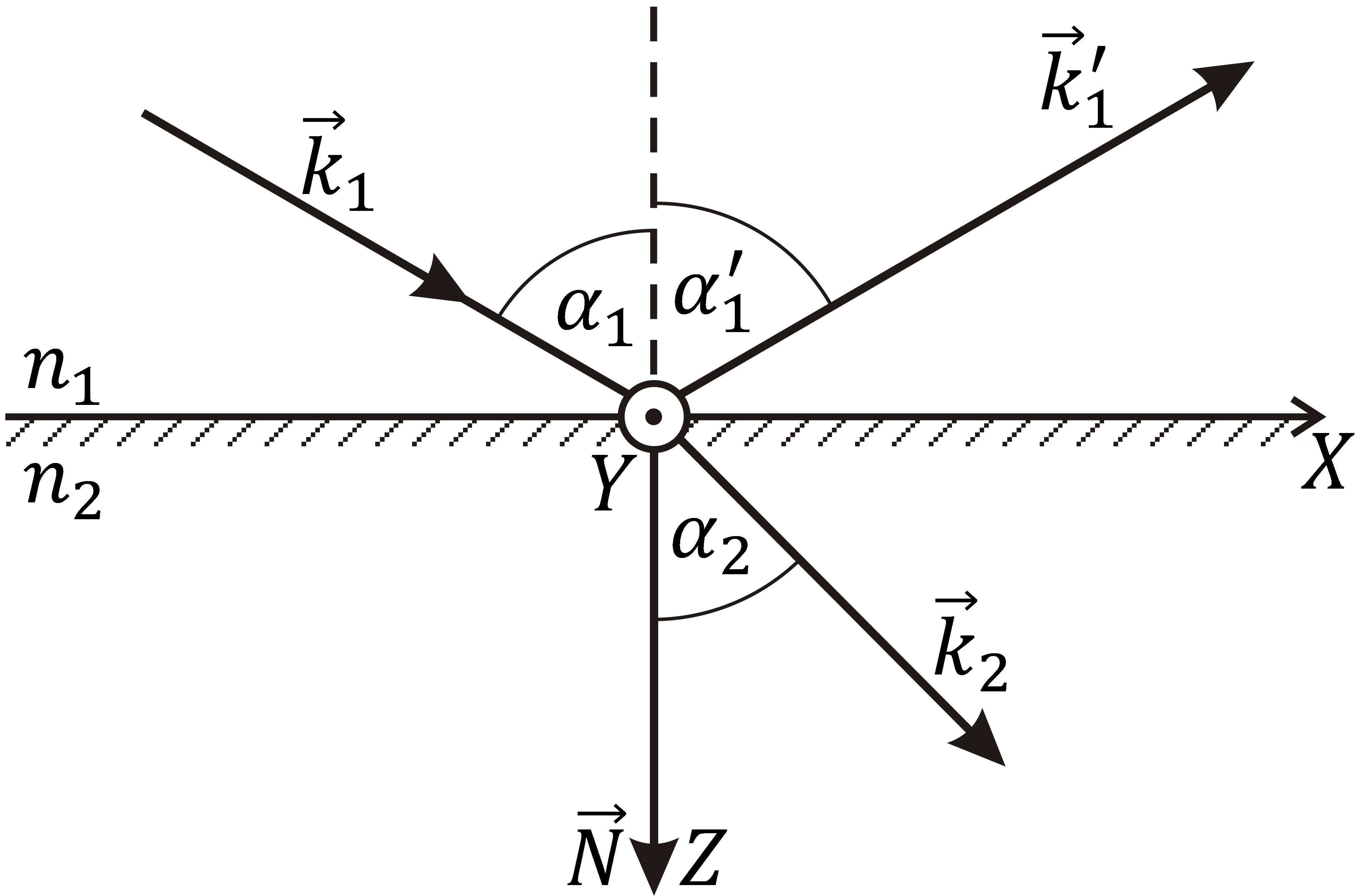
Поместим на границе раздела сред начало системы координат XYZ, совместив с этой границей координатную плоскость XY, направив ось Z внутрь второй среды, а оси X и Y – так, чтобы плоскость падения совпала с координатной плоскостью XZ (рис. 9.1). Запишем первое граничное условие – равенство тангенциальных составляющих напряженности электрического поля E_t на границе раздела, т.е. при z = 0. Выражая волны E, E₁ и E₂ через координаты, т.е. заменив k₁×r на и т.д., где x, y, z – координаты точки падения луча, и зная, что для падающей волны k_1y = 0, а также, что E_t⁽¹⁾ равно сумме тангенциальных составляющих вектора E падающей и отраженной волн, будем иметь

(9.1)

Равенство (9.1) должно тождественно выполняться в любой момент времени t. Это означает, что параметр t не должен входить в это равенство, т.е. должен быть исключен из этого соотношения. Для этого необходимо, чтобы показатели экспонент, содержащие параметр t, были одинаковыми, а значит, должны быть одинаковыми и коэффициенты при t: Таким образом, частоты отраженной и преломленных волн равны частоте падающей волны. Но так и должно быть, так как эти волны представляют собой результат сложения вторичных волн, излучаемых атомами и молекулами среды при вынужденных колебаниях их электронов, вызываемых падающей волной. На языке фотонной теории равенство частот отраженного, преломленного и падающего света означает, что при падении фотона на границу раздела сред он не расщепляется на два (проходящий и отраженный), его индивидуальность как частицы сохраняется.

Для выполнения граничного условия (9.1) во всех точках поверхности раздела (при всех значениях x и y) в равенство (9.1) не должны входить координаты x и y; они должны быть исключены из этого соотношения. Для этого необходимо, чтобы зависимость E_t от координат точек плоскости XY у всех трех волн была одинаковой, а значит, должны быть одинаковыми и показатели экспонент, содержащие переменные x и y. Это требование будет выполнено, если проекции волновых векторов на плоскость XY будут равны, т.е. если

(14.1)

Из первых равенств (9.1) вытекает, что векторы k¢₁ и k₂ лежат в плоскости падения y = 0. Следовательно, лучи падающий, отраженный и преломленный лежат в одной плоскости, в которой лежит также нормаль N к границе раздела сред. Из рис. 14.1, а видно, что

При этом

Тогда из равенства находим, что откуда Получен закон отражения: угол отражения равен углу падения.

Из равенства получаем закон преломления (называемый также законом Снеллиуса):

Согласно этому закону отношение синуса угла падения к синусу угла преломления равно отношению фазовой скорости волны в первой среде к фазовой скорости волны во второй среде или отношению показателя преломления сред, в которых распространяются луч преломленный и луч падающий. Величина называется относительным показателем преломления (второй среды по отношению к первой).

Из закона преломления видно, что если то Среду с бо́льшим показателем преломления называют оптически более плотной. Таким образом, волновой вектор расположен под меньшим углом к нормали N в той среде, которая является оптически более плотной. Луч, попадая в оптически более плотную среду, отклоняется в сторону нормали к границе раздела сред, а попадая в оптически менее плотную – в сторону от нормали.

Закон преломления часто записывают в симметричной относительно обеих сред форме:

(9.2)

Это равенство называют инвариантом преломления. Из этой симметрии следует обратимость световых лучей: если из среды 2 направить луч под углом к нормали к границе раздела сред, т.е. вдоль луча – k₂, то преломленный луч будет распространяться в среде 1 под углом к нормали, т.е. вдоль луча – k₁.

При малых углах падения и преломления ( синусы углов (15.7) можно заменить самими углами (в радианах), и в этом случае инвариант преломления примет вид

(9.3)

В частном случае нормального падения луча на границу раздела

Рис. 9.2

сред имеем – луч проходит во вторую среду, не преломляясь.

Законы отражения и преломления света лежат в основе геометрической оптики. Они широко используются в расчетах различных оптических приборов и устройств..

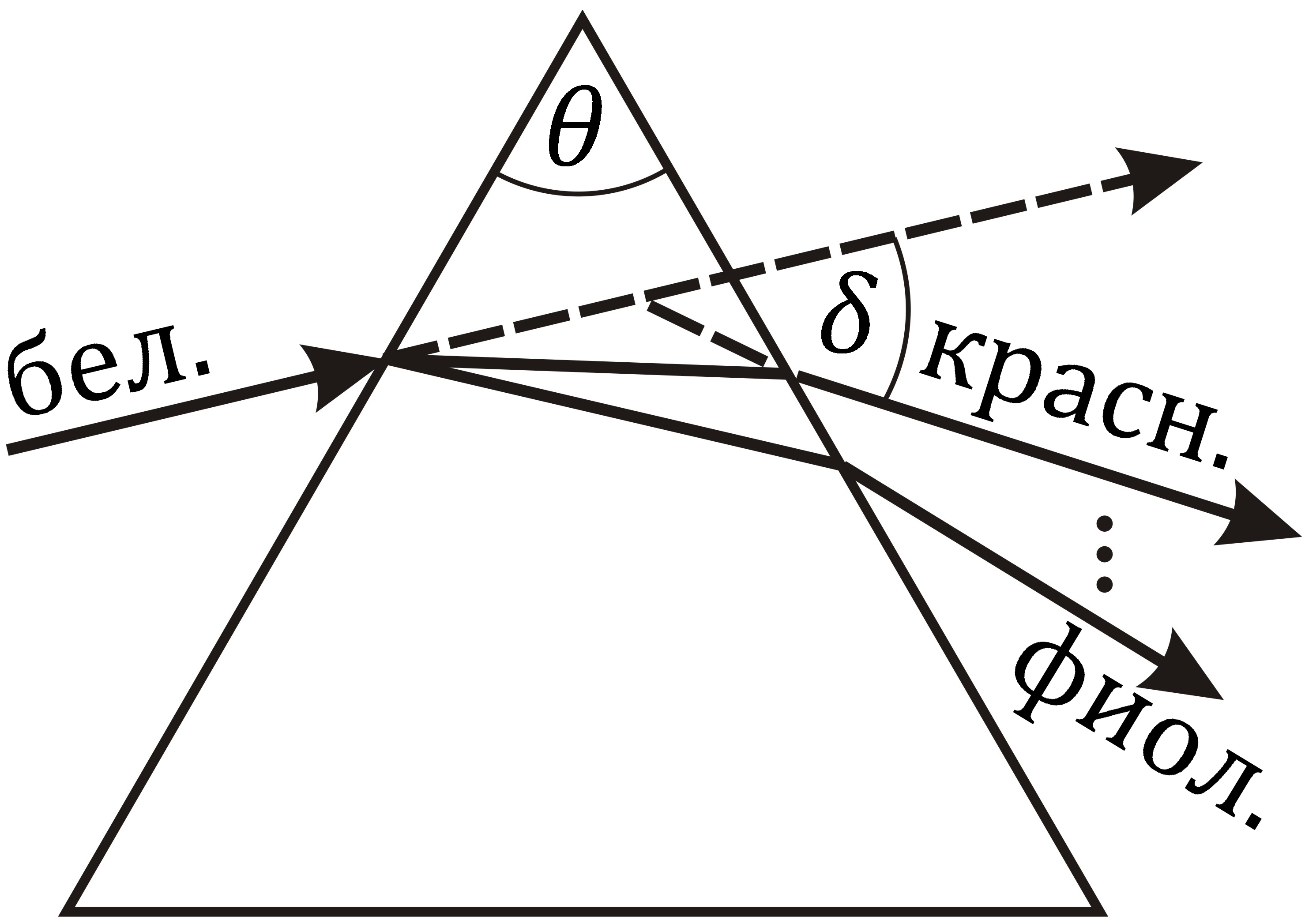
В качестве примера применения закона преломления света получим формулу (8.9). На рис. 9.2 показан ход лучей в призме. Из рисунка следует, что

(9.4)

так как Будем считать призму тонкой (угол мал) и малым угол падения . В этом случае будут малы и все остальные углы. Тогда, используя закон преломления в форме (9.3), можно записать С учетом этого находим

откуда

Подставляя это выражение в соотношение (14.4), приходим к формуле (8.9).

Если призма с показателем преломления n₁ находится в среде с показателем преломления, n₂, то под n в формуле (13.9) следует понимать относительный показатель преломления призмы: