9.2.2. Понятие о квантовой теории дисперсии света

В квантовой теории дисперсии, как и в классической, задача сводится к вычислению дипольного момента p(t), который возникает в атоме, находящемся в переменном электрическом поле световой волны. Как и при рассмотрении классической теории дисперсии будем считать, что атом обладает одним оптическим электроном. Предположим, что атом до того, как он оказался в электрическом поле световой волны, находился в одном из своих квантовых состояний с энергией W_n и волновой функцией y ⁰_n(r, t). При включении внешнего поля его состояние изменится (в нем будут возникать вынужденные колебания). Возникшее состояние будет характеризоваться волновой функцией y_n(r, t), которую можно найти из решения уравнения Шредингера методом теории возмущений. Возмущением является работа сил электрического поля, совершаемая над электроном в предположении, что поле слабое. При этом поскольку внешнее электрическое поле гармонически меняется во времени с частотой w, то и возникшее состояние атома также будет меняться во времени с той же частотой. Появится переменный дипольный момент атома, индуцированный электрическим полем световой волны. Его среднее значение, определяемое как , оказывается линейно зависящем от поля. Определив дипольный момент, можно вычислить и диэлектрическую проницаемость вещества в осциллирующем поле световой волны.

В общем случае в дисперсию дают вклад как невозбужденные атомы (на уровне W₁), так и возбужденные (на уровнях W_m > W₁). Невозбужденные атомы могут участвовать лишь в переходах, сопровождающихся поглощением света. Для таких переходов силы осцилляторов принято считать положительными. Возбужденные атомы могут участвовать в переходах двух типов: возможны переходы с этого возбужденного уровня на более высокие энергетические уровни и переходы на ниже расположенный уровни. Переходы второго типа сопровождаются испусканием света и они изменяют показатель преломления в противоположном направлении по сравнению с поглощением. Это обстоятельство может быть отражено в формулах, если силам осцилляторов, связанных с излучательными переходами приписать противоположный, т.е. отрицательный знак.

Вид дисперсионной формулы будет несколько различаться в зависимости от того, находились ли все атомы до включения поля в основном состоянии или часть атомов находилась в основном состоянии, а часть в возбужденном. Если все атомы среды до возникновения поля световой волны находились в основном состоянии, то дисперсионная формула будет иметь вид (13.7). Хотя дисперсионные формулы в классической и квантовой теории имеют одинаковый вид, их интерпретации различны. В классической теории частоты являются собственными частотой колебаний атомного осциллятора. В квантовой теории значения пропорциональны разностям энергий возможных переходов атома из основного состояния с энергией W₁ в возбужденное состояние с энергией W_m, и определяются совокупностью энергий стационарных состояний атома: W₁, W₂, W₃, …, W_m, … , W_n, … В квантовой механике, как видим, даже одноэлектронный атом имеет несколько собственных частот. Поэтому и в квантовой дисперсионной формуле появляется множитель Индекс m в квантовой теории определяет не номер осциллятора (в квантовой теории представление об атомных осцилляторах не используется) а номер стационарного состояния атома. Силы осцилляторов в квантовой теории определяется не экспериментально, а вычисляются теоретически и представляют собой величины, пропорциональные вероятностям указанных переходов атома : . Силы осцилляторов нормированы так, что их сумма равна числу электронов на внешней оболочке атома (т.е. числу валентных электронов). Суммирование в формуле (13.7) в квантовой теории ведется по всем стационарным состояниям m атома.

Если часть атомов среды перед началом действия светового поля находилась в возбужденном состоянии, то дисперсионная формула примет вид

(8.9)

где – частоты атомных переходов, определяемых уровнями энергии стационарных состояний атома: W₁, W₂, W₃, …, W_m, … , W_n, …, 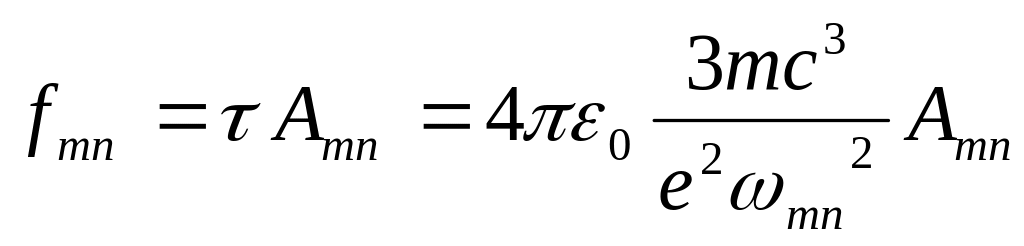– сила осциллятора с частотой соответствующая переходу атома между стационарными состояниями m и n (при этом ), вероятность спонтанного перехода атома с уровня m на уровень n, N_m – концентрация атомов, находящихся в m-состоянии. Силу осциллятора можно выразить и через матричный элемент дипольного момента p атома и частоту перехода Очевидно, что – полная концентрация атомов. Кроме того, при наличии возбужденных состояний они могут увеличивать отрицательное поглощение (индуцированное излучение) и изменять дисперсию так, что число осцилляторов уменьшается в соответствии с дополнительным множителем На этот множитель следует умножить силу осциллятора в формуле (8.9).

При комнатной температуре почти все атомы находятся в нормальном состоянии и, следовательно, дисперсия вещества будет описываться формулой (8.7).

По квантовым представлениям области аномальной дисперсии возникают при частотах, соответствующих переходам электронов из основного в возбужденные состояния с учетом квантовых правил отбора. Эти области имеют ширину порядка естественной ширины атомных уровней. Области же нормальной дисперсии имеют размер порядка частоты перехода электрона из основного (W₁) в возбужденное (W_n) состояние (n > 1).