8.7. Разрешающая способность объектива

Как уже отмечалось, изображение удаленной светящейся точки, даваемое даже идеальной (без аберраций) оптической системой формирования изображения (одной линзой или объективом), вследствие дифракции света на оправе линзы или на входном зрачке (диафрагме) объектива представляет собой не точку, а целую дифракционную картину в виде светового кружка (кружка Эри), окруженного чередующимися темными и светлыми кольцами

Представим себе теперь две близко расположенные друг к другу точки S₁ и S₂ какого-либо протяженного предмета и рассмотрим сначала изображение этого предмета, даваемое одной линзой. Если эти точки являются некогерентными источниками, то испускаемые ими световые волны не интерферируют, и в плоскости изображения происходит сложение не амплитуд волн, а их интенсивностей. Поэтому изображение точек представляет собой простое наложение дифракционных картин от отдельных точек. Будем считать, что изображаемый предмет находится на большом удалении от линзы. В этом случае лучи, идущие в линзу от каждой точки S₁ и S₂, можно считать параллельными, а дифракцию на линзе – фраунгоферовой. Если расстояние между центрами их изображений мало по сравнению с размерами кружков Эри, то результирующая картина практически не будет отличаться от картины, представляющей изображение одной точки; изображения точек наложатся друг на друга и дадут одно неравномерно освещенное световое пятно. Следовательно, две очень близкие точки будут изображаться даже идеальной линзой не как две раздельные точки, а как одна точка. В таком случае говорят, что линза не разрешает рассматриваемые точки. Как бы ни было велико по размерам изображение предмета, на нем не будут видны соответствующие детали; изображение предмета будет не резким, размытым.

Если увеличивать расстояние между изображаемыми точками, то расстояние между центрами их изображений также будет увеличиваться при неизменном угловом размере соответствующих им кружков Эри. Начиная с некоторого расстояния между точками, на графике суммарного распределения интенсивности посередине появится провал, т.е. разделяющая дифракционные пятна более темная полоса. Интенсивность света в провале будет отличаться от максимального значения на относительную величину где Если величина этого провала достигнет 20% от максимальной интенсивности, то такая картина будет восприниматься как раздельное изображение двух точек. В этом случае говорят, что линза разрешает точки S₁ и S₂.

Вместо глубины провала часто пользуются контрастом изображения, под которым понимают отношение разности максимального и минимального значений интенсивности к их сумме, т.е. величину

При этом двадцати процентному провалу соответствует одиннадцати процентный контраст. Действительно, так как = то и тогда

Все сказанное в полной мере относится и к системе линз, заключенных в оправу, т.е. к объективу. Возможность объектива

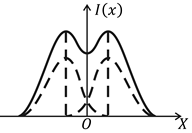
строить раздельно изображение двух близко расположенных точек объекта называют его разрешающей способностью. Количественный критерий разрешающей способности объектива был предложен Рэлеем. Согласно Рэлею, изображения двух точечных некогерентных источников считаются разрешенными (находятся на пределе разрешения), если центральный максимум интенсивности дифракционной картины изображения одного из них совпадет с первым дифракционным минимумом другого (рис. 9.12). В этом случае провал на кривой суммарного распределения интенсивности даже превышает указанное выше значение 20%. Действительно, радиальное распределение интенсивности в изображении точки описывается функцией

где z = 2R / . Первый нуль этой функции имеет место при

Рис. 9.12

z₁ = 3,93. При выполнении критерия Рэлея кривые, описывающие центральные максму-

мы двух картин, пересекаются в точке z = z₁ / 2 = 1,915. Значение функции I(z) в этой точке равно 0,37I(0), поэтому интенсивность в провале составляет 237% = 74% от максимальной интенсивности. При этом величина провала составляет 26% от максимальной интенсивности.

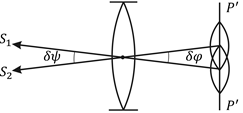
Обозначим через  (рис. 9.13) наименьшее угловое расстояние между двумя точками (стрелками на рис. 9.13 показаны нап-

Рис. 9.13

равления на эти точки), при котором они еще разрешаются объективом. Эту величину называют угловым разрешением. Так как аберрации, вносимые объективом, не учитываются, а учитывается только дифракция света на оправе объектива, то указанную величину  называют также дифракционным пределом разрешения. Величина R, обратная , называется разрешающей силой объектива:

R = 1/.

Найдем эту величину. На рис. 9.13 видно, что критерий Рэлея будет выполняться, если угловое расстояние  между точками S₁ и S₂ окажется равным угловому размеру кружка Эри  = 1,22 / /D, где D – диаметр оправы линзы или диаметр апертурной диафрагмы объектива, т.е. если  =  = 1,22 / D. Отсюда получаем разрешающую силу объектива:

(8.23)

Как видим, разрешающая сила объектива тем больше, чем больше диаметр D его апертурной диафрагмы и чем меньше длина волны применяемого для освещения предмета света.

Формула (9.29) применима к объективам фото- и киноаппарата, зрительной трубы, телескопа. Например, для лучшего российского телескопа с диаметром объектива D ≈ 6 м расчет по вышеприведенной формуле дает для наименьшего углового расстояния между звездами

рад.

(Расчет проведен для средней длины волны мкм.) Предел разрешения оптической системы зависит от многих факторов: длины волны света, размеров и геометрии линз, а также от типа системы формирования изображения.

Глаз при рассматривании удаленных предметов действует принципиально так же, как объектив телескопа, поэтому формула (12.1) применима и к глазу; роль D здесь играет диаметр зрачка глаза. Поскольку диаметр зрачка глаза D ≈ 3 мм, то, полагая  = = 0.510 ^{– 6} мкм, получим  = 210 ^{- 4} рад ≈ 0,7. Следовательно, минимальное угловое расстояние между двумя удаленными на большое расстояние от глаза точками, при котором глаз воспринимает их раздельно как две точки, примерно равно одной угловой минуте. Полученный результат хорошо согласуется с физиологической оценкой разрешающей способности глаза (расстояние между соседними светочувствительными элементами сетчатки глаза соответствует этому угловому расстоянию). Этот пример демонстрирует удивительную способность живого организма приспосабливаться к окружающим условиям и в процессе эволюции достигать максимума того, что принципиально допускается законами природы.

Увеличение окуляра оптического прибора должно подбираться так, чтобы дифракционные кружки, разрешенные объективом, были разрешены и глазом, т.е. были видны под углом около 1. При фотографировании объекта линейное расстояние между центрами дифракционных картин двух близко расположенных точек должно превосходить размеры зерен эмульсии, что соответствует расстояниям порядка 0,01 мм.

1 Отсюда русское слово «икона».

1 Подробно об этом будет говориться в п. 10.6.