8.6. Тонкая линза

8.6.1. Формула тонкой линзы

В качестве примера применения принципа Ферма получим формулу тонкой линзы. Линза является простейшей центрированной оптической системой, формирующей оптическое изображение. Центрированными системами называются системы, у которых пограничные поверхности отражающих и преломляющих тел представляют собой поверхности вращения с общей осью, или, в частности, сферические поверхности, центры которых лежат на одной прямой (оптической оси). Такие системы используются для получения оптического изображения.

Линза – прозрачное тело (обычно стеклянное), ограниченное двумя сферическими или плоской и сферической поверхностями. Линза является основным элементом любой оптической системы (фотоаппарат, кино- и телекамера, микроскоп, телескоп). Линза называется тонкой, если ее максимальная толщина d₀ много меньше радиусов кривизны R₁ и R₂ сферических образующих линзу поверхностей. В тонкой линзе поперечным смещением луча можно пренебречь и считать, что луч, входящий в точке с координатами x, y на одной поверхности линзы выходит в точке приблизительно с такими же координатами на противоположной поверхности.

Тонкая двояковыпуклая линза изображена на рис. 10.6. Здесь O – центр линзы, C₁ и C₂ – центры кривизны ограничивающих линзу сферических поверхностей. Прямая, проходящая через центр линзы O и центры кривизны C₁ и C₂, называется оптической осью линзы. Любой луч, походящий через центр линзы O, не преломляется, так как угол преломления здесь равен нулю.

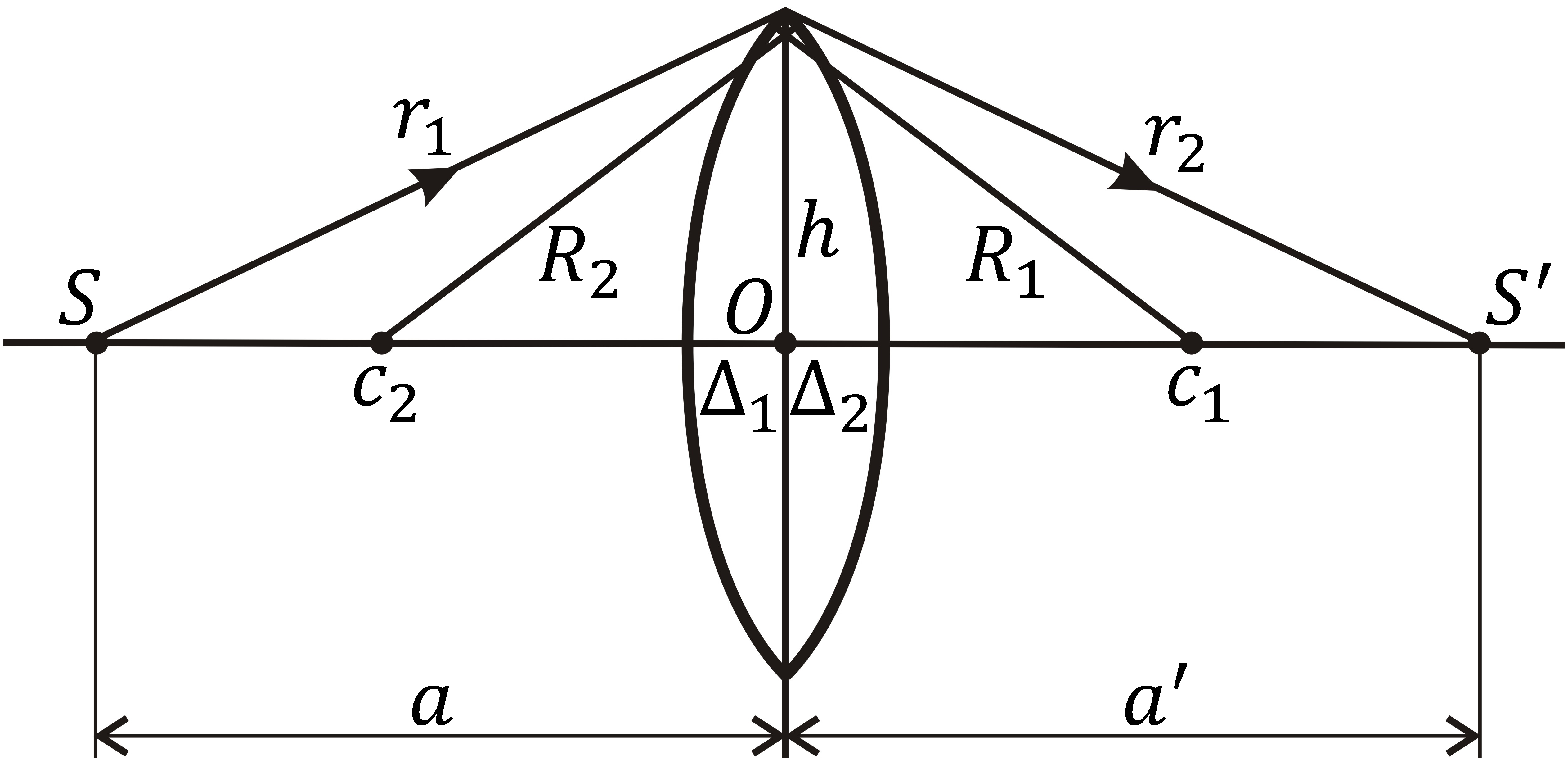
Рис. 7.6

Пространство, расположенное перед линзой – это пространство предметов, а за линзой – пространство изображений. Все величины, относящиеся к пространству предметов, обозначаются не штрихованными символами, а к пространству изображений – штрихованными.

Получим формулу, связывающую расстояния от предмета до линзы (a), от линзы до изображения с величинами, характеризующими линзу: радиусами кривизны ее поверхностей R₁ и R₂ и показателем преломления n.линзы. Эту формулу называют формулой линзы. Для ее получения используем принцип Ферма. Пусть S – светящаяся точка, лежащая на оптической оси на расстоянии a от линзы, а S – ее изображение, расположенное на оптической оси на расстоянии a от линзы.

Все лучи, исходящие из точки S и прошедшие через линзу, собираются в сопряженной точке S. В соответствии с принципом Ферма, оптические длины всех лучей, выходящих из источника S и приходящих в ее изображение S, будут одинаковы. Рассмотрим два из этих лучей: один, идущий вдоль оптической оси, а второй – через край линзы. Будем считать, что линза находится в воздухе, показатель преломления которого приблизительно равен единице. Показатель преломления материала линзы n. Тогда оптическая длина крайнего луча, распространяющегося в воздухе, будет равна просто геометрической длине

а луча, идущего вдоль оптической оси – соответственно

Из рис. 10.6 находим . Откуда, учитывая, что линза тонкая, и вследствие этого членом можно пренебречь, получаем Аналогичным образом находим В геометрической оптике обычно используют параксиальное приближение (т.е. рассматривают лучи, проходящие вблизи оптической оси). В этом приближении

По принципу Ферма . Приравнивая оптические пути, получим

или

(10.25)

где

Соотношение (10.25) и есть формула линзы. Величина Ф называется оптической силой линзы.

В оптике принята следующая система знаков: все расстояния отсчитываются от центра линзы, за положительное направление принимается направление распространения луча слева направо. Радиус кривизны поверхности линзы считается положительным, если поверхность обращена выпуклой стороной к падающему пучку и отрицательным – если вогнутой. Тогда для рассматриваемой здесь двояковыпуклой линзы , а . С учетом этого имеем

(10.26)

формулу линзы (7.25) можно записать в виде

. (10.27)

Из (7.27) видно, что если , то , если же , то . Следовательно, пучок параллельных лучей, идущих справа налево вдоль оптической оси от бесконечно удаленного источника, сходится в точке , а пучок таких же лучей, идущих слева направо, – в точке . Наоборот, если , то , если же то , т.е. лучи исходящие из точек и после преломления в линзе идут параллельно оптической оси линзы. На основании этого, исходя из определения фокусов центрированной оптической системы, можно сделать вывод, что точки и являются фокусами линзы. Расстояние, определяемое равенством , является фокусным расстоянием. Фокус F, расположенный перед линзой, называется передним фокусом, а фокус F, расположенный за линзой, – задним фокусом. Если среда перед линзой и за линзой имеет одинаковый показатель преломления (как в рассматриваемом случае), фокусы F и F расположены симметрично относительно плоскости линзы. Плоскость, проходящая через передний фокус перпендикулярно оптической оси линзы, называется передней фокальной плоскостью, а проходящая через задний фокус – задней фокальной плоскостью. Заменив в формуле (10.26) Ф на , запишем ее в виде

. (10.28)

При ( ) линза является собирающей, а при

Рис. 7.7

( ) – рассеивающей. Первую линзу называют также положительной, а вторую – отрицательной. Положительной линзой является, например, двояковыпуклая линза, а отрицательной – двояковогнутая линза. Это следует из формулы (10.26). Действительно, для двояковыпуклой линзы кривизна левой ограничивающей сферической поверхности отрицательна, а правой – положительна, т.е. , и тогда Ф > 0, f > 0; для двояковогнутой линзы , и Ф < 0, f < 0.

Свойства фокусов можно использовать для получения изображения B точки B, не лежащей на оптической оси. Для этого из точки B следует провести лучи 1 и 2 до пересечения с линзой – луч 1 параллельно оптической оси, а луч 2 – через передний фокус F. Луч 1 после преломления пройдет через задний фокус F, а луч 2 – параллельно оптической оси (рис. 10.7. Точка пересечения этих лучей B и даст изображение точки B. Как видим, для построения изображения достаточно взять только два луча. В качестве второго луча (в дополнение к лучу 1 или 2) можно использовать луч 3, проходящий через центр линзы O. Этот луч проходит через линзу не преломляясь. Из этого построения, рассматривая подобные треугольники ABF и ODF, ABF и OCF, находим , где x, z и x, z – координаты точек B и B в системах координат с центрами в фокусах. Откуда получаем

.

Эта формула является частным случаем формулы (10.22), когда фокусные расстояния f и f по модулю равны. Введя систему координат с началом в центре линзы и с осью Z, направленной вдоль луча света (слева направо), и учтя, что придем к формуле линзы в виде (10.27). Отношение представляет собой линейный коэффициент увеличения линзы. При изображение прямое, а при – перевернутое. Из того же рис. 10.7 видно, что