8.4. Следствия из основного уравнения

геометрической оптики

Рассмотрим сначала случай оптически однородной среды, т.е. среды, в которой n(r) = const. Одним из возможных решений уравнения эйконала (10.7) в этом случае будет Ф(x, y, z) = = при условии, что Из уравнения (10.5) находим вектор луча: s = Это – прямая линия. Отсюда следует, что световые лучи в оптически однородных средах представляют собой параллельные прямые с направляющими косинусами а поверхности равной фазы (волновые поверхности) – плоскости, ортогональные лучам.

Другое возможное решение основного уравнения геометрической оптики в оптически однородной среде получается, когда эйконал Ф является функцией расстояния Ф = Ф(r). Так как то уравнение (10.7) в этом случае будет иметь вид

.

Решением этого уравнения при n = const будет Ф(r) = nr, если s = r / r. Следовательно, лучи света в этом случае представляют собой семейство радиальных прямых, расходящихся из точки r = 0, а волновые поверхности nr = n = const – концентрические сферы с центром в той же точке r = 0.

Тем самым мы снова показали, что в оптически однород-

Рис. 7.2

ной среде свет распространяется прямолинейно (световые лучи – прямые линии). Видим также, что закон прямолинейного распространения света является одним из следствий основного уравнения геометрической оптики.

Если среда, в которой распространяется свет, не является оптически однородной, т.е. если ее показатель преломления изменяется от точки к точке, то световые лучи будут искривлены. Свет будет распространяться не прямолинейно, а вдоль кривой, которая, как можно показать, будет изгибаться в область с большим показателем преломления. При скачкообразном изменении показателя преломления (что имеет место на границе раздела двух различных оптически однородных сред) скачком будет изменяться и направление распространения лучей – лучи будут преломляться. Получим закон преломления света

Будем исходить из соотношения (10.9). Обозначим показатели

преломления сред через n₁ и n₂. Направления падающего и прелом- ленного лучей будем определять соответственно векторами s₁ и s₂ (рис. 10.2). Выберем узкий прямоугольный контур abcda, пересекающий границу раздела сред (на рис 10.2 показан пунктиром). Применяя соотношение (10.9) к этому контуру, будем иметь

Переходя к пределу при ab ® 0 и cd ® 0 и учитывая, что в каждой среде получим (n₁s₁) × l₁ + (n₂s₂) × l₂ = 0. Но l₂ = – l₁ и тогда (n₁s₁ – n₂s₂) × l₁ = 0. Отсюда следует, что вектор (n₁s₁ – n₂s₂) перпендикулярен вектору l₁, т.е. перпендикулярен границе раздела сред. Поэтому, обозначив через N единичный вектор нормали к границе раздела сред, можно записать N (n₁s₁ – n₂s₂) = 0 или

n₁ (N s₁) = n₂ (N s₂). (10.11)

Соотношение (10.11) показывает, что преломленный луч s₂ лежит в той же плоскости, что и падающий луч s₁ и перпендикуляр N к границе раздела сред – первая часть закона преломления. Переписав равенство (10.11) в скалярном виде и учтя, что N, s₁ и s₂ – единичные векторы, получим вторую часть закона преломления:

(10.12)

где и – углы, образуемые падающим и преломленным лучами с нормалью к поверхности раздела сред, называемые углами падения и преломления соответственно.

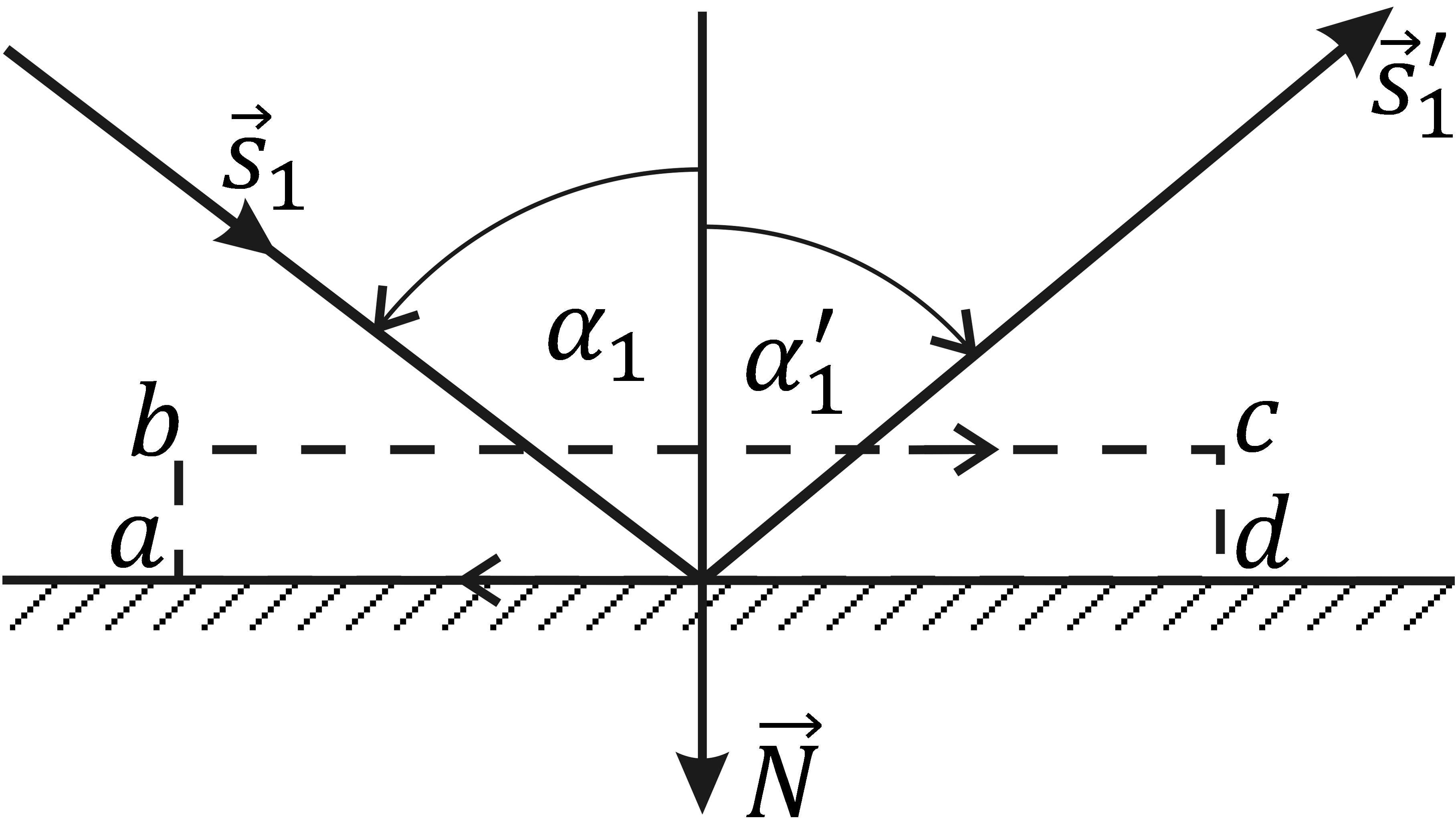
Для получения закона отражения света контур abcda следует провести, как показано на рис. 10.3. В этом случае вместо (10.11) будем иметь

N s₁ = N s¢₁ , (10.13)

где s¢₁ – вектор отраженного луча. Из соотношения (10.13) непосредственно вытекает закон отражения: луч падающий s₁

отраженный s¢₁ и перпендикуляр N к границе раздела сред лежат в одной плоскости, а угол падения равен углу отражения В геометрической оптике при отсчете углов и от перпендику-

Рис. 7.3

ляра к границе раздела сред направление по часовой стрел- ке считается положительным, а против часовой стрелки – отрицательным. Поэтому закон отражения записывают в виде = – . Заметим, что отражение света можно рассматривать как частный случай преломления обратно в первую среду. Поэтому закон отражения можно получить из (10.12) формальной подстановкой n₂ = – n₁.

Приведенные выводы законов преломления и отражения света являются наиболее общими, так как они справедливы для лучей любой формы, а не только для прямолинейных лучей; необходимо лишь, чтобы выполнялось условие применимости геометрической оптики, т.е. условие малости длины волны.

Что касается закона независимого распространения световых лучей, то с точки зрения геометрической оптики он справедлив, когда интерференцией лучей можно пренебречь.