7.6.3. Дифракция на щелевой решетке белого света

Из соотношения d sin = m видно, что положения главных максимумов, кроме центрального (m = 0), в дифракционной картине от щелевой решетки зависят от длины волны используемого света . Поэтому если решетка освещается белым или другим немонохроматическим светом, то для разных значений  все дифракционные максимумы, кроме центрального, окажутся пространственно разделенными. В результате в дифракционной картине решетки, освещаемой белым светом, центральный максимум будет иметь вид белой полосы, а все остальные – радужных полос, называемых дифракционными спектрами первого (m =  1), второго (m =  2) и т.д. порядков. В спектрах каждого порядка наиболее отклоненными будут красные лучи (с большим значением , так как sin  1 / ), а наименее – фиолетовые (с меньшим значением ). Спектры получаются тем более четкими (в смысле разделения цветов), чем больше щелей N содержит решетка. Это следует из того, что линейная полуширина максимума обратно пропорциональна числу щелей N). Максимальное число наблюдаемых дифракционных спектров определяется соотношением (3.83). Таким образом, дифракционная решетка производит разложение сложного излучения на отдельные монохроматические составляющие, т.е. проводит гармонический анализ падающего на него излучения.

Свойство дифракционной решетки разлагать сложное излучение на гармонические составляющие используется в спектральных аппаратах – приборах, служащих для исследования спектрального состава излучения, т.е. для получения спектра излучения и определения длин волн и интенсивностей всех его монохроматических компонент. Принципиальная схема спектрального аппарата приведена на рис. 6. Свет от исследуемого источника попадает на входную щель S прибора, находящуюся в фокальной плоскости коллиматорного объектива L₁. Образующаяся при прохождении через коллиматор плоская волна падает на диспергирующий элемент D, в качестве которого используется дифракционная решетка. После пространственного разделения лучей диспергирующим элементом выходной (камерный) объектив L₂ создает монохроматическое изображение входной щели в излучении разных длин волн в фокальной плоскости F. Эти изображения (спектральные линии) в своей совокупности и составляют спектр исследуемого излучения.

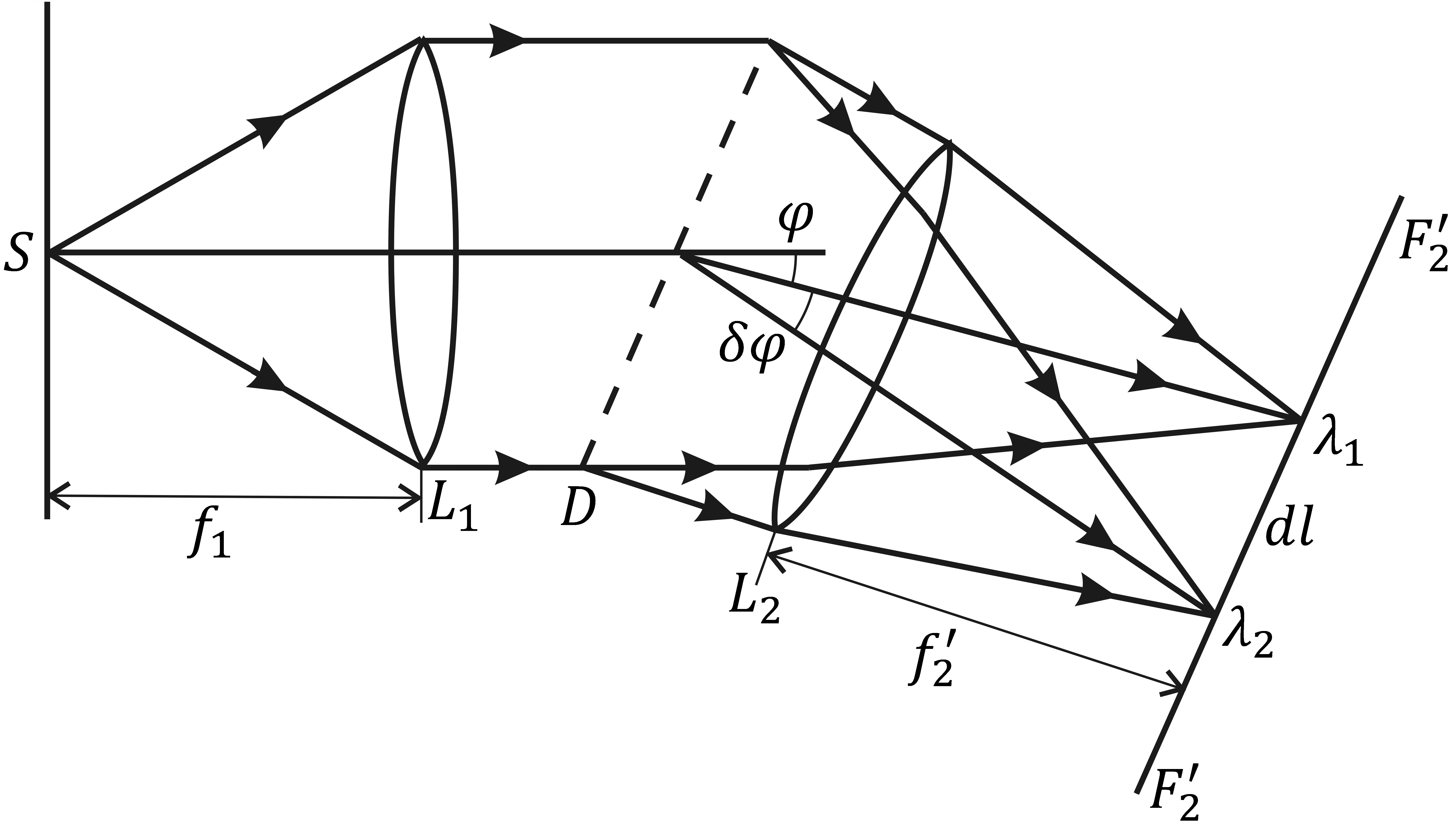
Рис. 7.

Как спектральный прибор дифракционная решетка характеризуется угловой и линейной дисперсией, свободной областью дисперсии и разрешающей способностью. Как спектральный прибор дифракционная решетка характеризуется угловой и линейной дисперсией, свободной областью дисперсии и разрешающей способностью.

Угловая дисперсия D_ характеризует изменение угла отклонения  луча при изменении его длины волны  и определяется как

D_ = d / d,

где d - угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на d. Дифференцируя соотношение d sin = m, получим d cos _ = m, откуда

D_ = _ = m / d cos.

В пределах небольших углов cos  1, поэтому можно положить

D_  m / d.

Линейная дисперсия определяется выражением

D_l = dl / d,

где dl – линейное расстояние между двумя спектральными линиями, отличающимися по длине волны d.

Из рис. 3.24 видно, что dl = f₂ d, где f₂ – фокусное расстояние объектива L₂. С учетом этого получаем соотношение, связывающее угловую и линейную дисперсии:

D_l = f₂ D_.

Спектры соседних порядков могут перекрываться. Тогда спектральный аппарат становится непригодным для исследования соответствующего участка спектра. Максимальная ширина  спектрального интервала исследуемого излучения, при которой спектры соседних порядков еще не перекрываются, называется свободной областью дисперсии или дисперсионной областью спектрального аппарата. Пусть длины волн падающего на решетку излучения лежат в интервале от  до  + . Максимальное значение , при котором перекрытия спектров еще не происходит, можно определить из условия наложения правого конца спектра m-го порядка для длины волны  +  на левый конец спектра

(m + 1)-го порядка для длины волны , т.е. из условия

d sin = m( + ) = (m + 1),

откуда

 =  / m.

Разрешающая способность R спектрального прибора характеризует способность прибора давать раздельно две близкие спектральные линии и определяется отношением

R =  /  ,

где   – минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются как раздельные спектральные линии. Величину   называют разрешаемым спектральным расстоянием. Вследствие дифракции на действующем отверстии объектива L₂ каждая спектральная линия изображается спектральным аппаратом не в виде линии, а в виде дифракционной картины, распределение интенсивности в которой имеет вид sinc²-функции. Так как спектральные линии с различ-

Рис. 3.25

ными длинами волн не когерентны, то результирующая дифракционная картина, создаваемая такими линиями, будет представлять собой простое наложение дифракционных картин от каждой щели в отдельности; результирующая интенсивность будет равна сумме интенсивностей обеих линий. Согласно критерию Рэлея, спектральные линии с близкими длинами волн  и  +   считаются разрешенными, если они находятся на таком расстоянии  , что главный дифракционный максимум одной линии совпадает по своему положению с первым дифракционным минимумом другой линии. В этом случае на кривой суммарного распределения интенсивности (рис. 3.25) образуется провал (глубиной, равной 0,2I₀, где I₀ – максимальная интенсивность, одинаковая для обеих спектральных линий), что и позволяет глазу воспринимать такую картину как двойную спектральную линию. В противном случае две близко расположенные спектральные линии воспринимаются как одна уширенная линия.

Положение m-го главного дифракционного максимума, соответствующего длине волны , определяется координатой

x_m = f tg  f sin = m f / d.

Аналогично находим и положение m-го максимума, соответствующего длине волны  +  :

x_m = m( +  ) f / d.

При выполнении критерия Рэлея расстояние между этими максимумами составит

x = x_m - x_m= m  f / d

равно их полуширине  x = f / d (здесь, как и выше, полуширину мы определяем по первому нулю интенсивности). Отсюда находим

  =  / (mN),

и, следовательно, разрешающая способность дифракционной решетки как спектрального прибора

R = mN.

Таким образом, разрешающая способность дифракционной решетки пропорциональна числу щелей N и порядку спектра m. Положив

m = m_max  d / ,

получим максимальную разрешающую способность:

R_max = ( / )_max = m_maxN  L / ,

где L = Nd – ширина рабочей части решетки. Как видим, максимальная разрешающая способность щелевой решетки определяется только шириной рабочей части решетки и средней длиной волны исследуемого излучения. Зная R_max, найдем минимально разрешимый интервал длин волн:

( )_min   ² / L.