6.7. Дифракция Френеля на щели

Щелью называют прямоугольное отверстие, один из размеров которого (длина) много больше другого (ширины).

Предположим, что щель, ширина которой равна а, равномерно освещается нормально падающим монохроматическим пучком света с длиной

волны  и амплитудой E₀. Совместим с плоскостью щели координатную плоскость XY и ориентируем ее так, чтобы ось X была направлена перпендикулярно краям щели (вдоль размера а); ось Y параллельно краям, а начало координат О поместим в точку, расположенную посередине щели (рис. 6,, а).

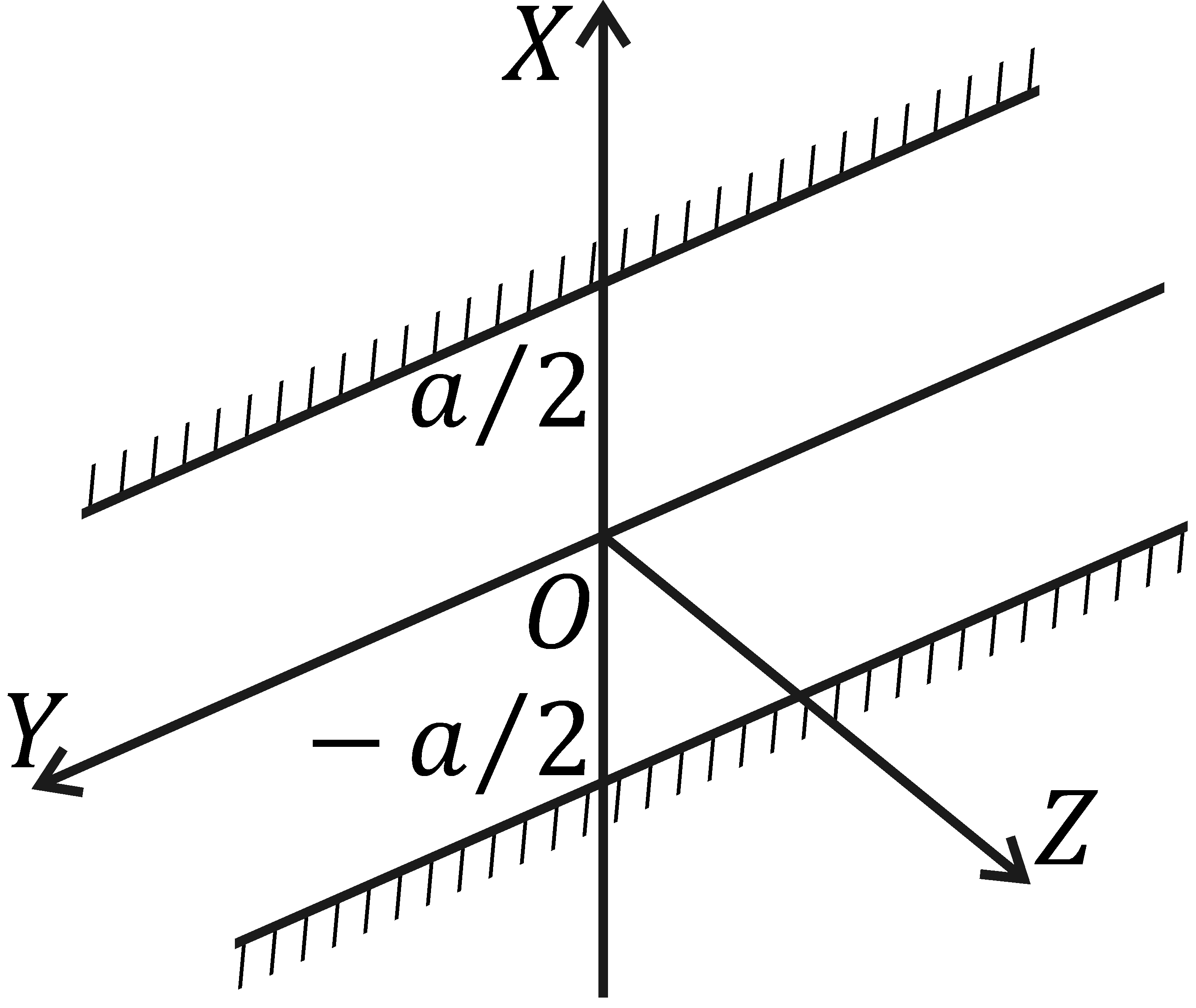
а) б)

Рис. 6.16

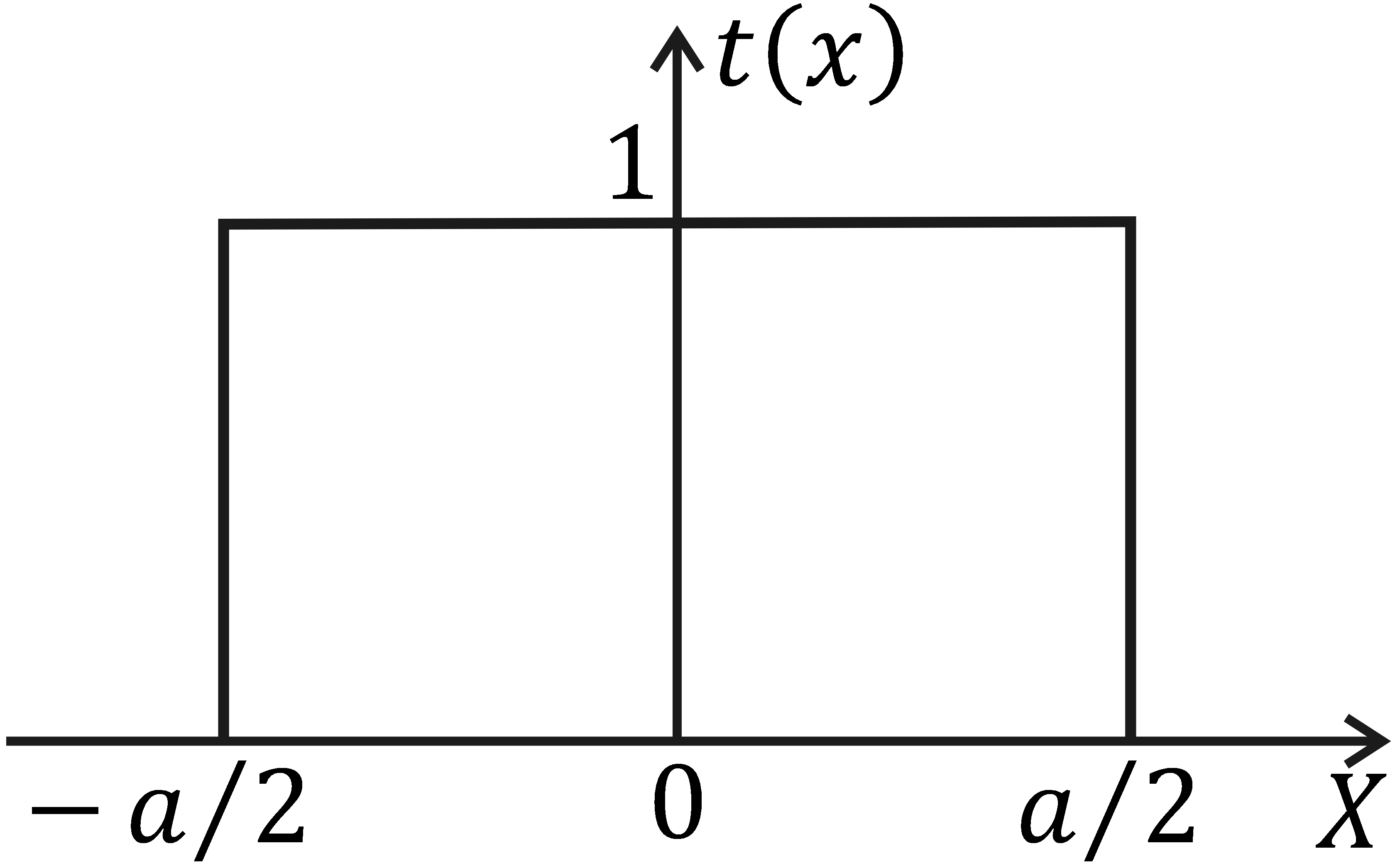
Апертурная функция щели будет зависеть только от одной переменной (x) и в выбранной системе координат будет иметь вид

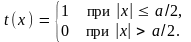(6.)

Эта зависимость имеет вид прямоугольника высотой, равной единице и стороной основания, равной а (рис. 6.б).

Бесконечно длинную щель можно рассматривать как две обращенные в разные стороны полуплоскости (края двух протяженных экранов; один край (нижний) расположен вдоль прямой 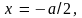а другой (верхний) – вдоль прямой 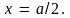). Следовательно, задача о дифракции Френеля на щели может быть решена с помощью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу (рис. 6).

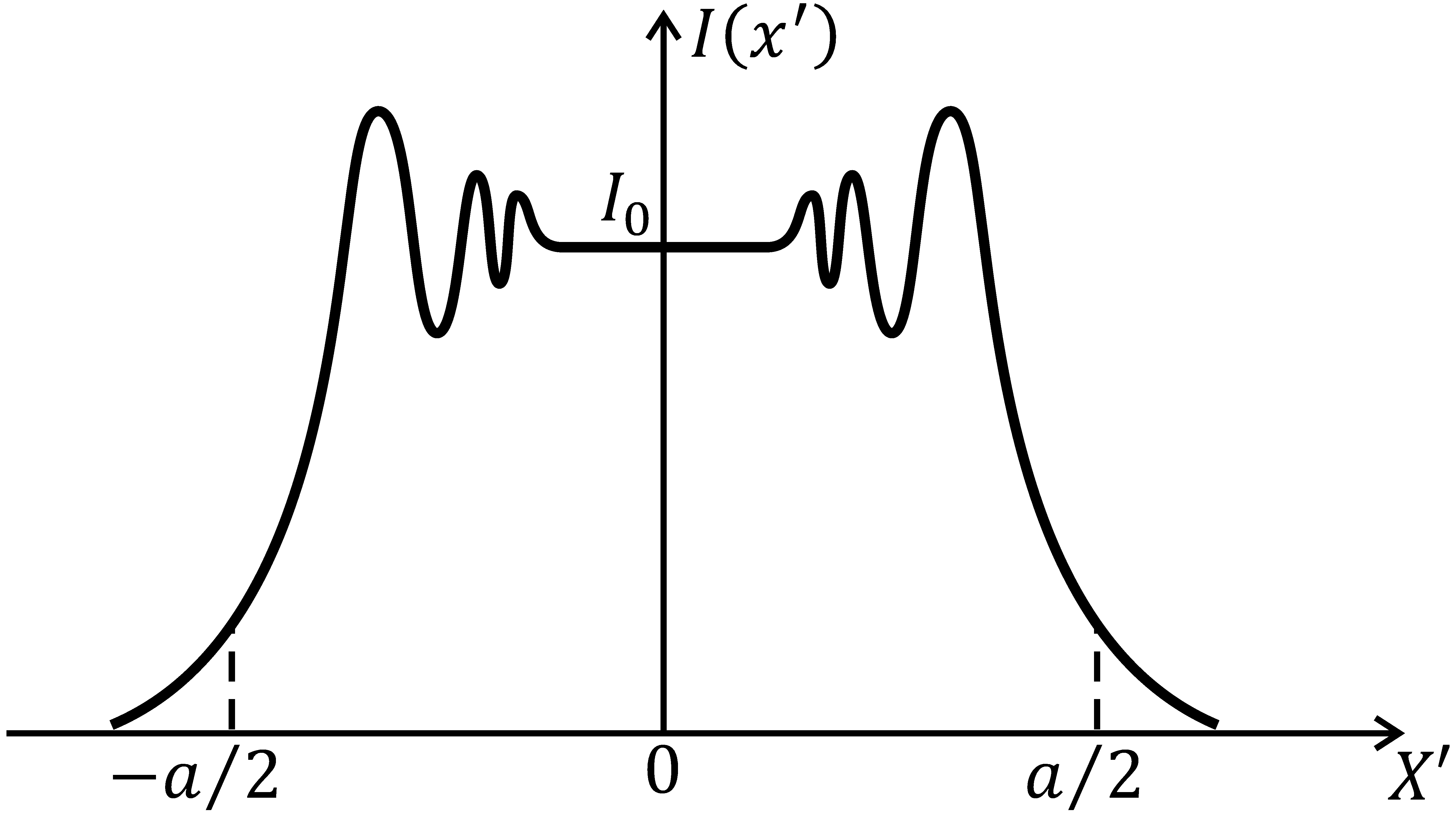
Рис. 6.17

Построенная с помощью спирали Корню кривая распределения интенсивности в дифракционной картине, приведена на рис. 6.

Характер результирующей дифракционной картины определяется дифракцией на двух противоположных краях щели и падающей на щель плоской волной. Вид зависимости интенсивности результирующего поля от координаты x′ существенно зависит Юот ширины щели, т.е. от соотношения между шириной щели a и расстоянием до нее z, точнее от безразмерного параметра .

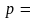
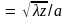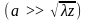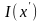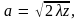_{При большой ширине щели} распределение интенсивности световой волны в области напротив середины щели практически постоянно. Дифракционные полосы наблюдаются на экране напротив краев щели (рис. 6.). Зависимость при малой ширине щели, когда показана на рис. 6. Видим, что при такой ширине щели в центре дифракционной картины находится светлая полоса без каких-либо заметных колебаний интенсивности. Быстро затухающие колебания интенсивности происходят лишь в области геометрической тени при

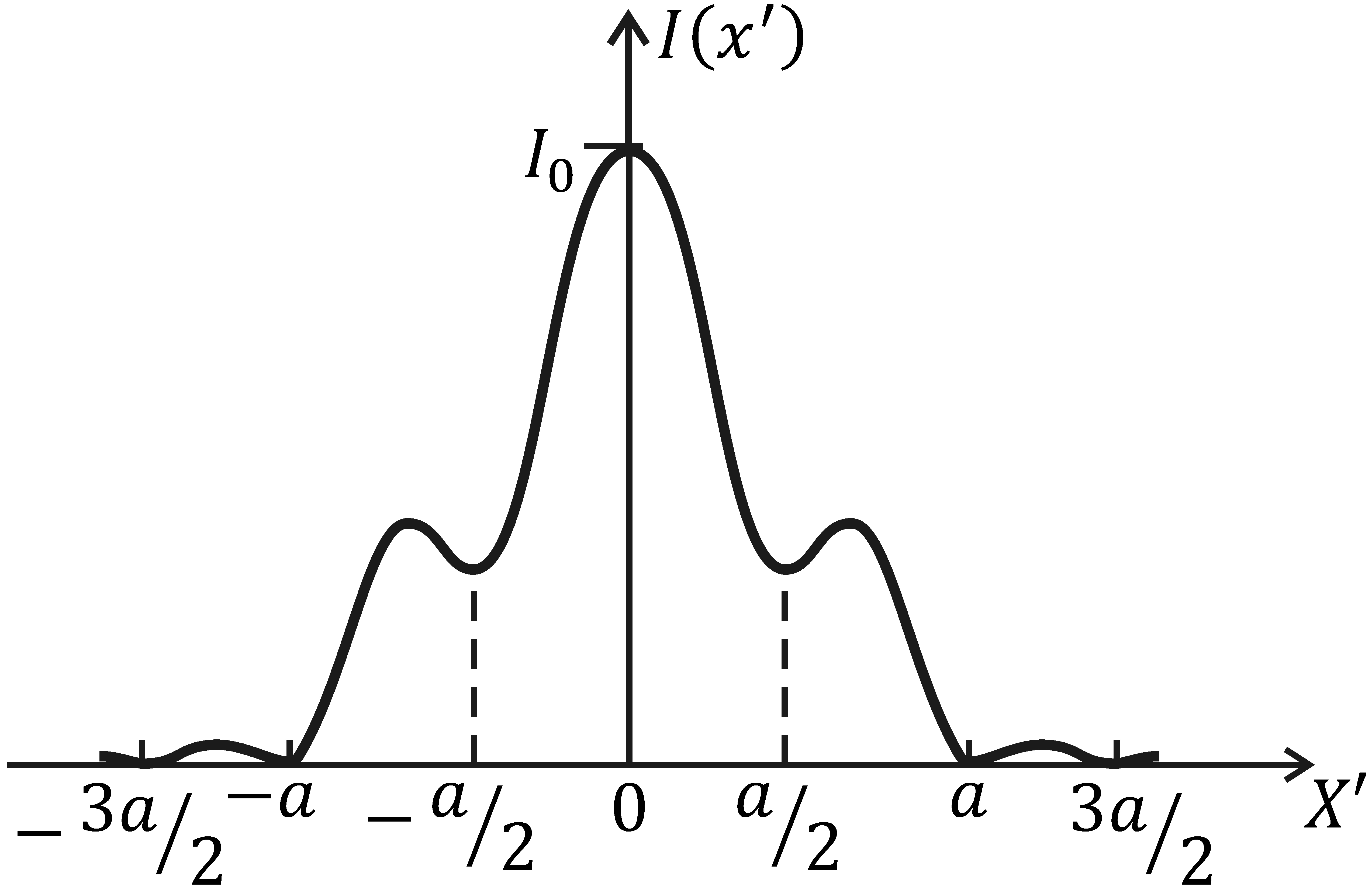
Рис. 6.18

Следует отметить, что в зависимости от параметра р при френелевой дифракции на щели центральная полоса может быть не только светлой, но и относительно темной.