- •Глава 6
- •Дифракция света. Дифракция френеля
- •6.1. Определение дифракции. Виды дифракции
- •Для определения светового поля в точке р фронт волны ф(t)
- •Линии пересечении этих сфер с фронтом волны будут границами указанных кольцевых участков, а сами эти участки – зонами Френеля в рассматриваемом случае сферического волнового фронта.
- •6.3. Дифракция Френеля на круглом отверстии и
- •6.4. Зонные пластинки
- •6.6. Дифракция Френеля на крае полуплоскости
- •6.7. Дифракция Френеля на щели
6.6. Дифракция Френеля на крае полуплоскости
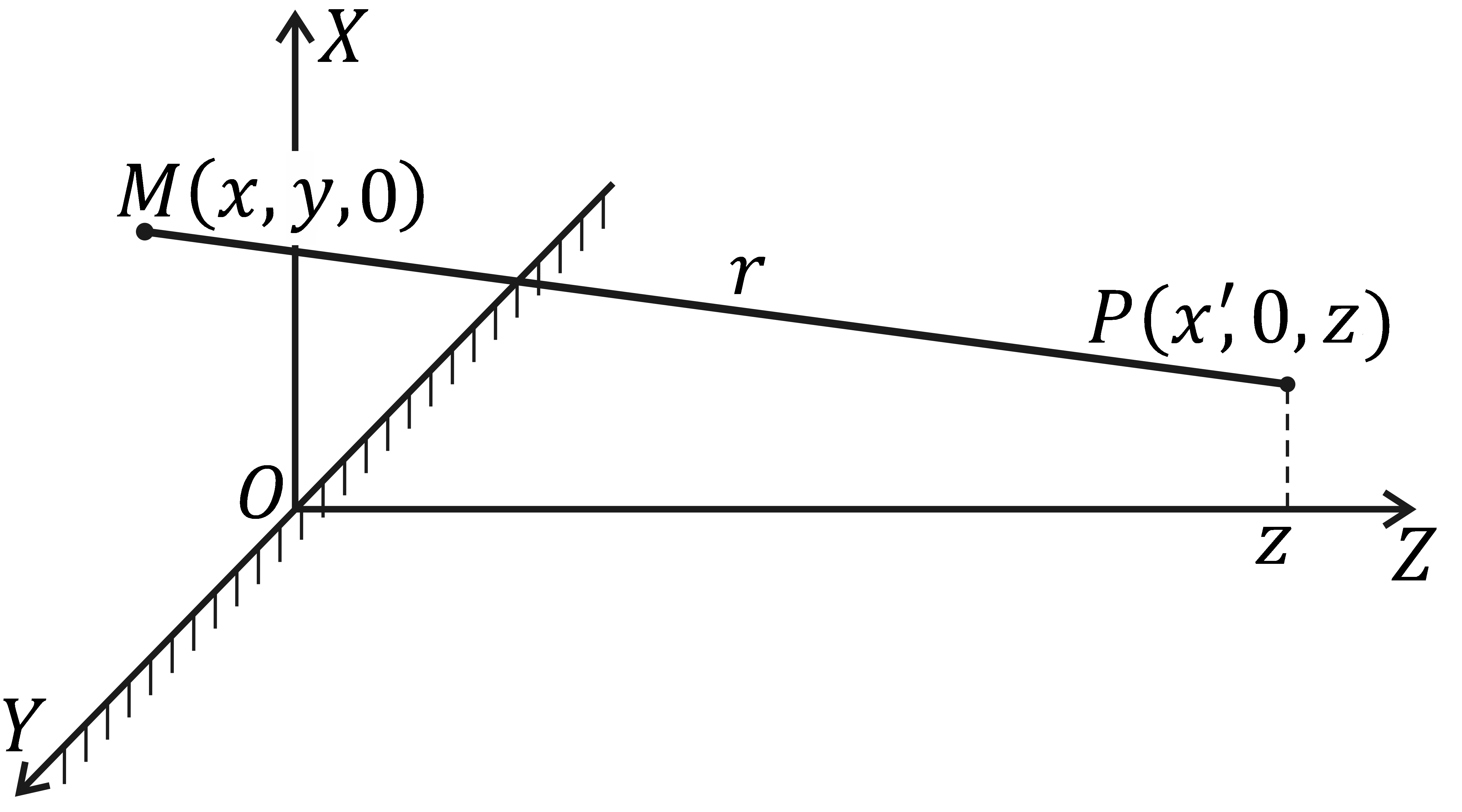
Используя графический метод, решим практически важную задачу определения интенсивности света вблизи границы тени, отбрасываемой прямолинейным краем протяженного экрана (полуплоскости) при падении на него сферической волны. Совместим с плоскостью экрана координатную плоскость XY, направив ось X перпендикулярно краю, а ось Y вдоль его (рис. 5.6). В выбранной системе координат апертурная функция экрана
t(x,
y)
= t(x)
=

(Функция такого вида в математике называется функцией скачка, функцией Хэвисайда или единичной функцией и обозначается как 1(x); следовательно, t(x) = 1(x)).
Разобьем
открытую часть поверхности сферического
волнового фронта плоскостями,
параллельными краю экрана (рис. 6).
Волновой фронт при этом разделится на
отдельные прямоугольные полоски (зоны).
Ширину зон выберем так, чтобы отсчитанные
в плоскости рисунка расстояния от точки
наблюдения Р
до краев любой зоны отличались на
одинаковую величину ∆.
При этом условии колебания, создаваемые
в точке Р
соседними зонами, будет отличаться по
фазе на постоянную величину δ
= k∆
. При
таком построении площади зон оказываются
отличными друг от друга. Они убывают
сначала быстро, а затем очень медленно.
Убедимся в этом. Из рис. 6 видно, что
суммарная ширина первых
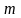 зон
равна
зон
равна
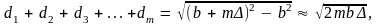
Рис. 6.13 |
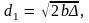 а отношение ширин выбранных таким
образом зон к ширине первой зон
а отношение ширин выбранных таким
образом зон к ширине первой зон

Это отношение изменяется так же, как ряд чисел:
1,00:0,41:0,32:0,23:0,22: …
Такое соотношение размеров зон приводит к тому, что ломаная линия, получающаяся при графическом сложении колебаний, оказывается довольно сложной. Вначале она идет более полого, чем в случае кольцевых зон (площади которых при аналогичном построении примерно равны), а затем (когда площади соседних зон становятся примерно одинаковыми) переходят в спираль, фокус которой смещен относительно начала координат. Если ото-
двинуть край экрана влево (рис.6.) и просуммировать колебания, приходящие от открывающихся зон, то получится левая часть кривой, которая будет симметрична рассмотренной (правой). Эту сложную кривую – клотоиду называют спиралью Корню; ее график представлен на рис 6. Аналитические выражения, описывающие такую кривую, называют интегралами Френеля. Эти интегралы имеют вид
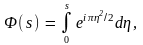
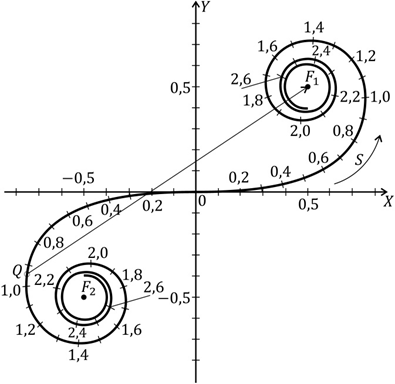
Рис. 6.14
Представив комплексное подынтегральное выражение в виде

интеграл Френеля можно привести к двум интегралам вида
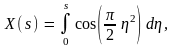

Их тоже называют интегралами Френеля.
Спираль
Корню строится следующим образом.
Строится координатная плоскость XY,
на которой наносятся точки с координатами

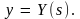 При непрерывном изменении параметра s
эти точки образуют гладкую кривую, вид
которой и показан на рис. 6. Числа,
отмеченные вдоль спирали, дают значения
параметра s.
При непрерывном изменении параметра s
эти точки образуют гладкую кривую, вид
которой и показан на рис. 6. Числа,
отмеченные вдоль спирали, дают значения
параметра s.
Поскольку
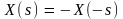 и
и
 то спираль Корню симметрична относительно
начала координат. Как видно из рис. 6.,
она состоит из двух симметричных ветвей,
закручивающихся вокруг точек F1
и F2,
называемых фокусами спирали. К этим
точкам асимптотически приближается
кривая при стремлеии s
к
то спираль Корню симметрична относительно
начала координат. Как видно из рис. 6.,
она состоит из двух симметричных ветвей,
закручивающихся вокруг точек F1
и F2,
называемых фокусами спирали. К этим
точкам асимптотически приближается
кривая при стремлеии s
к
 Поэтому координаты фокусов можно найти,
положив
Поэтому координаты фокусов можно найти,
положив
 Тогда получим
Тогда получим
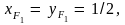
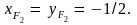
Обозначим
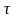 – угол между касательной к спирали
Корню и осью X.
Тогда, учитывая, что
– угол между касательной к спирали
Корню и осью X.
Тогда, учитывая, что
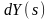
 будем иметь
будем иметь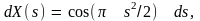


Следовательно,
 (8.*)
(8.*)
Отсюда
видно, что при
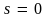 угол
угол
 т.е. в начале координат кривая касается
оси X.
При
т.е. в начале координат кривая касается
оси X.
При
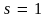 угол
угол
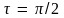 – касательная к кривой Корню перпендикулярна
оси X.
При
– касательная к кривой Корню перпендикулярна
оси X.
При
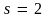 угол
угол
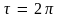 – касательная параллельна оси X,
принимая исходное горизонтальное
направление. При
– касательная параллельна оси X,
принимая исходное горизонтальное
направление. При
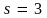 угол
угол
 – касательная снова перпендикулярна
оси X
и т.д. Формула (8.*) позволяет наглядно
проследить, как кривая обвивается вокруг
фокусов F1
и F2,
делая при этом бесконечное число
оборотов. Эта формула позволяет также
по заданному параметру s
легко находить соответствующую точку
на спирали Корню. Параметр s
находится, зная на экране расстояние x
точки наблюдения от центра дифракционной
картины О.
– касательная снова перпендикулярна
оси X
и т.д. Формула (8.*) позволяет наглядно
проследить, как кривая обвивается вокруг
фокусов F1
и F2,
делая при этом бесконечное число
оборотов. Эта формула позволяет также
по заданному параметру s
легко находить соответствующую точку
на спирали Корню. Параметр s
находится, зная на экране расстояние x
точки наблюдения от центра дифракционной
картины О.
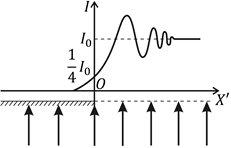
Применив спираль Корню к рассматриваемой нами задаче, получим кривую распределения интенсивности света в зависимости от расстояния x′ от края экрана (ось X направлена в плоскости экрана перпендикулярно краю вертикально вверх; начало ее помещено в точке, расположенной на крае экрана; ось X′ расположена в плоскости наблюдения и направлена параллельно оси X). Графически зависимость интенсивности I (x, 0) представлена на рис. 5.7, где I0 – интенсивность света при полностью открытом фронте, т.е. при отсутствии экрана. Видно, что резкой границы между светом и тенью нет.
В области геометрической тени (x 0) интенсивность не спадает резко до нуля, а убывает непрерывно и монотонно по закону
Рис. 6.15 |
 .
При x
= 0 интенсивность
I(0,
0) = I0
/ 4. В освещенной
же области (x
0) интенсивность
света не всюду равна I0,
а, осциллируя около этого значения,
постепенно приближается к I0.
При этом высота первого максимума над
уровнем I0
более чем на одну треть превышает
значение I0.
Следовательно, вблизи края протяженного
экрана в освещенной области возникает
дифракционная картина в виде чередующихся
светлых (убывающей освещенности) и
темных полос, параллельных краю экрана.
При этом с увеличением расстояния x
от края геометрической тени расстояние
между полосами уменьшается, полосы
сгущаются и становятся все менее
контрастными.
.
При x
= 0 интенсивность
I(0,
0) = I0
/ 4. В освещенной
же области (x
0) интенсивность
света не всюду равна I0,
а, осциллируя около этого значения,
постепенно приближается к I0.
При этом высота первого максимума над
уровнем I0
более чем на одну треть превышает
значение I0.
Следовательно, вблизи края протяженного
экрана в освещенной области возникает
дифракционная картина в виде чередующихся
светлых (убывающей освещенности) и
темных полос, параллельных краю экрана.
При этом с увеличением расстояния x
от края геометрической тени расстояние
между полосами уменьшается, полосы
сгущаются и становятся все менее
контрастными.