6.4. Зонные пластинки

Выше было показано, что в случае круглого отверстия, открывающего одну или небольшое нечетное число зон Френеля, амплитуда поля в точке наблюдения Р в два, а интенсивность в четыре раза больше, чем при полностью открытом волновом фронте. Интенсивность света I(P) = E(P) ² в точке Р можно во много раз увеличить, если на пути света из S в Р расположить экран который перекрывает все четные или все нечетные зоны Френеля. В этом случае вторичные волны от всех открытых зон Френеля будут приходить в точку Р в одинаковой фазе и в результате интерференции будут усиливать друг друга. Такой экран называют амплитудной зонной пластинкой (или решеткой) Френеля. Эта пластинка представляет собой систему концентрических чередующихся светлых и темных колец, построенных по принципу расположения зон Френеля, т. е. с радиусами _m колец, определяемыми выражением ((8.1) – для сферических волн и (8.5) – для плоских) для заданных значений a, b и  ( m – нечетное для прозрачных колец и m четное – для непрозрачных ). Простейшая амплитудная зонная решетка – это стеклянная пластинка, на которой (для определенных условий наблюдения, т.е. для определенных значений b и ) нанесены зоны Френеля – прозрачные и непрозрачные концентрические кольца. Действие амплитудной зонной пластинки описывается рядом (3.7), в котором оставлены члены только одного знака.

Еще больший эффект можно получить, если с помощью соответствующего экрана не перекрывать четные или нечетные зоны, а изменить фазы волн, приходящих от соседних зон на . В этом случае знакопеременный ряд (3.7) становится знакопостоянным с тем же числом членов N. Такой экран называют фазовой зонной пластинкой Вуда (рис. 3.5,б). В простейшем случае она представляет собой прозрачную пластинку, толщина которой в местах, соответствующих четным (или нечетным) зонам отличается на определенную величину h (сделаны выступы этой высоты). Такая пластинка называется профилированной пластинкой. Ее профиль изображен на рис. 9.,а. Таким же свойством будет обладать и ступенчатая прозрачная пластинка с высотой ступеньки h (рис.,б). Высоту ступеньки (выступа) h найдем из того условия, чтобы при прохождении через нее света он приобрел дополнительный набег фазы, равный :  = (2 / λ) = , где = nh – h = (n – 1) h – оптическая разность хода, возникающая при прохождении светом расстояния h в пластинке, n – показатель преломления материала пластинки. Будем иметь: h = λ / [2(n – 1)].

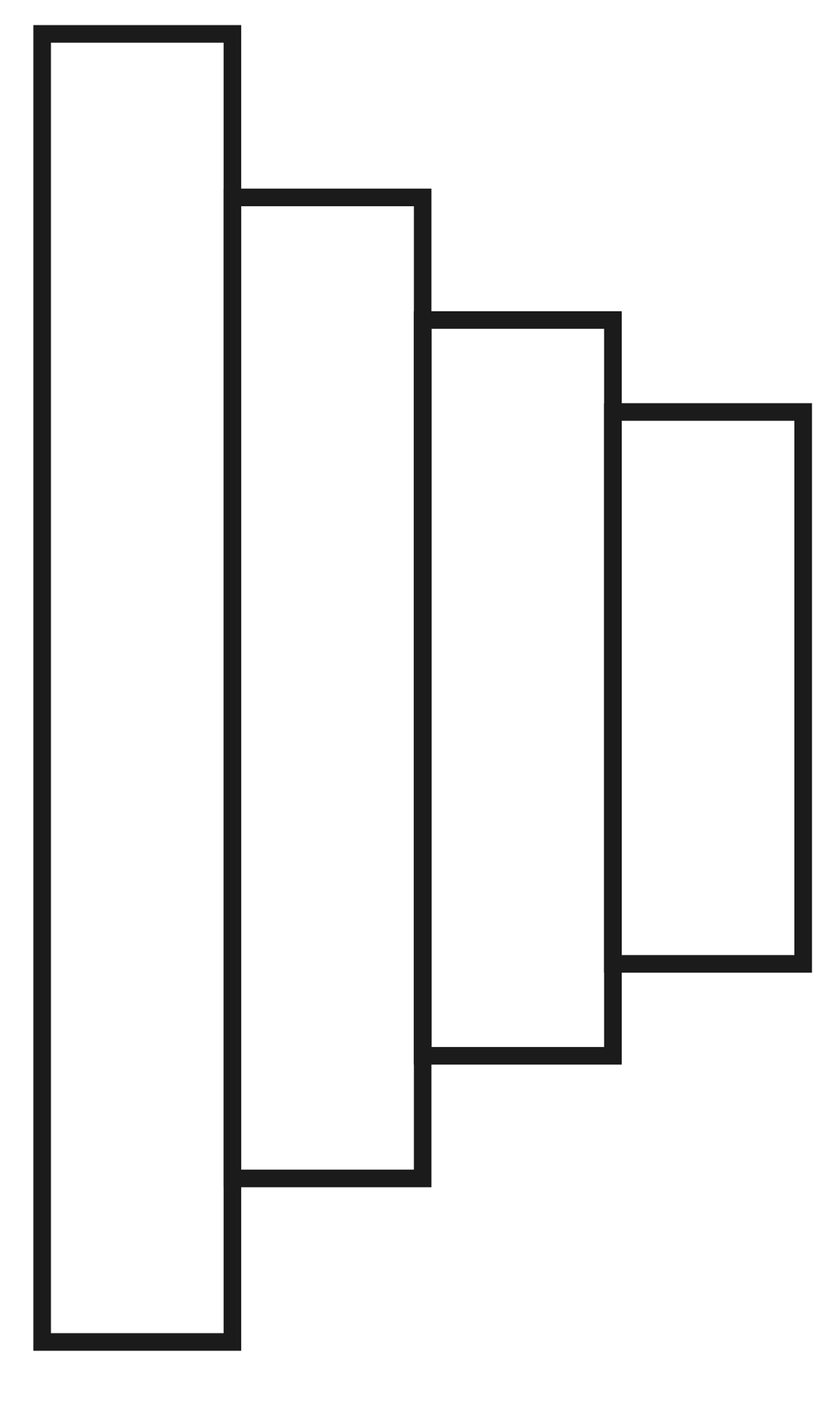
а) б) в)

Рис. 6.7

Максимальной интенсивности можно достичь с помощью фазовой пластинки с криволинейными профилями зон. Такая пластинка собирает весь падающий на нее свет в точке Р. Системы подобного типа называют плоскими линзами или растровой фокусирующей оптикой. Линзу можно рассматривать как фазовую пластинку с плавным криволинейным профилем.

Усиление интенсивности света зонной пластинкой аналогично фокусирующему действию линзы – в обоих случаях вторичные волны от всех точек волнового фронта приходят в точку Р в одинаковых фазах и в результате интерференции создают максимум интенсивности. При этом расстояния a и b от пластинки до точки S и до ее «изображения» Р связаны таким же соотношением, как и соответствующие величины для линзы. Действительно, формулу (3.1), связывающую расстояния a и b, можно представить в виде формулы линзы: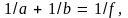 где «фокусное расстояние» f зонной пластинки определяется выражением

1 / f = m /_m².

Однако в отличие от линзы зонная пластинка имеет несколько фокусов (f зависит от m). При освещении пластинки с плоскими кольцами плоской волной ее фокусное расстояние найдется из формулы _m = .

С помощью зонной пластинки можно получать и оптические изображения. Однако поскольку разность фаз колебаний, обусловленных действием открытых зон Френеля, достигает в этом случае π, интерференционный максимум, создаваемый зонной пластинкой, не является острым. Поэтому изображения, даваемые зонной пластинкой, оказываются невысокого качества. (Качество получаемого на практике изображения существенно зависит также от степени монохроматичности используемого света, а также от того, сколь точно изготовлена пластинка). Условия интерференционного максимума выполняются для данной пластинки одновременно в нескольких точках, лежащих на ее оси. Концентрируя энергию волны в этих точках, зонная пластинка создает несколько изображений, что и позволяет говорить о нескольких «фокусных расстояниях» данной пластинки. Оптическое изображение можно получить и с помощью круглого отверстия радиуса, равного радиусу первой зоны Френеля. На этом свойстве узких отверстий основано действие темной фотокамеры, которой издавна пользовались для получения изображения без линз.

Найдем интенсивность света в точке фокусировки Р. Если радиус пластинки равен R, то число N зон Френеля, укладывающихся на пластинке, определится из условия R = _N = 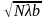, откуда N = R ² / (b). Число открытых зон равно (1 / 2) N = R ² / (2b). Каждая открытая зона создает в точке Р амплитуду, примерно равную E₁. Поэтому суммарная амплитуда в точке Р будет E = (N / 2)E₁ = E₁ ² / (2b). Но Е₁  2E₀, где E₀ – амплитуда плоской волны, падающей па пластинку. С учетом этого находим интенсивность в точке Р:

I = E ² = E₀ ² R ⁴ / (b) ² = I₀R ⁴ / (b) ².

Выигрыш в интенсивности составляет I / I₀ = R ⁴ / (b) ². Например, при R = 1см, b = 10 см и  = 0,5 мкм получаем I / I₀  410 ⁶, т.е. несколько миллионов.

На рис. 8.4, а изображена амплитудная зонная пластинка Френеля со светлым центром, у которой нечетные зоны оставлены прозрачными, а четные зачернены. Такая пластинка удаляет из волнового фронта все четные зоны Френеля. У нее внутренние радиусы колец пропорциональны квадратным корням из последовательных нечетных чисел, а внешние – из четных. При этом у светлых колец внутренние радиусы пропорциональны квадратным корням из последовательных четных чисел, а внешние – из нечетных Можно изготовить и аналогичную пластинку с темным центром.. Эта пластинка удаляет все нечетные зоны.

6.5. Графический способ построения дифракционных картин. Спираль Френеля

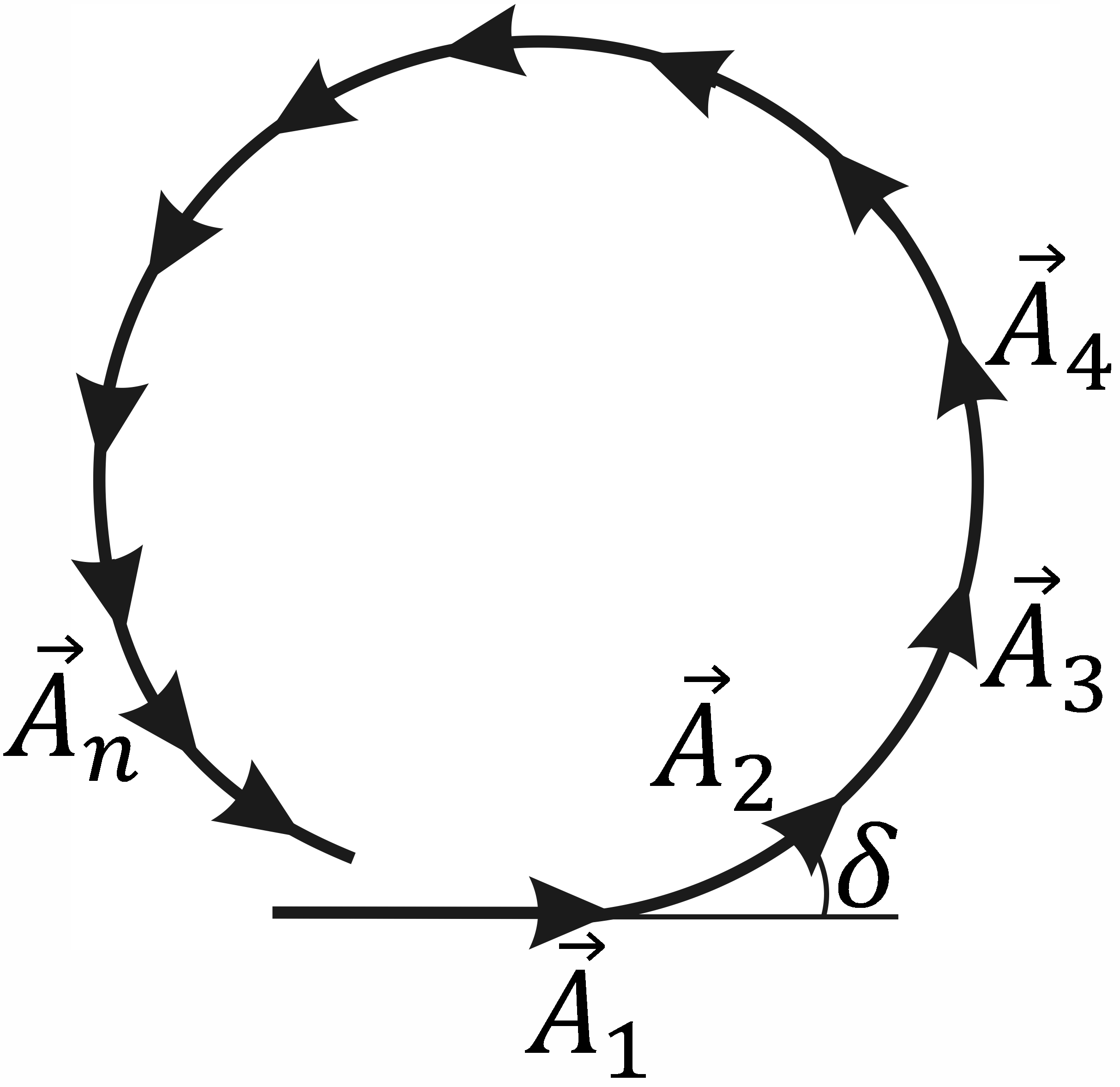
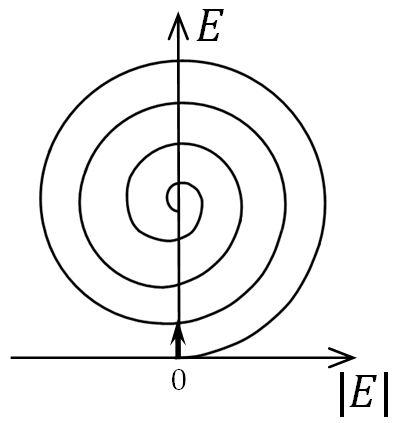
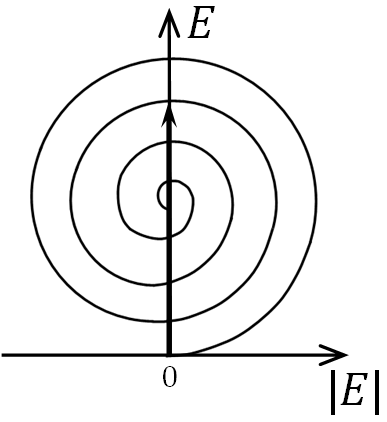
Указанный способ основан на методе векторных диаграмм, суть которого состоит в следующем. Разобьем фронт волны на большое число (в пределе бесконечно большое) концентрических колец – подзон, аналогичных зонам Френеля, но существенно меньших по ширине. При этом, очевидно, и каждая зона Френеля разделится на большое число подзон. Разность хода от краев соседних подзон будет одинаковой, но не равной  / 2, а составлять малую долю . Колебание, создаваемое в точке Р каждой из этих подзон, изобразим в виде вектора A_n (n = 1, 2, 3, …), длина которого равна амплитуде колебания, а угол, образуемый вектором A_n с направлением, принятым за начало отсчета (осью абсцисс, называемой базовой линией фазы), равен начальной фазе колебания. Поскольку углы здесь определяют фазу, а не направление, векторы A_n называют фазовыми векторами. Обычно за начало отсчета фазы принимают фазу колебания, создаваемого первой подзоной. Тогда векторы A₂, A₃, A₄, …, изображающие колебания от последующих подзон, будут составлять с вектором A₁ углы, равные разности фаз этих колебаний и колебания, создаваемого первой подзоной. Из способа построения подзон вытекает, что разность фаз колебаний от двух соседних подзон одинакова, поэтому каждый следующий вектор A_n будет повернут относительно предыдущего A_{n – 1} на один и тот же угол δ. Колебание, возбуждаемое нескольким соседними подзонами, представится суммой векторов A₁, A₂, A₃, … Построив векторную сумму, амплитуду результирующего колебания найдем как длину вектора, проведенного из начала первого вектора A₁ к концу последнего вектора A_n, а фазу результирующего колебания – как угол наклона этого вектора к оси абсцисс. Получающаяся при этом геометрическая фигура – векторная – диаграмма – имеет вид ломаной спиралевидной линии, изображенной на рис. 8. , а. Не замкнутость получающейся ломаной линии обусловлена тем, что амплитуды колебаний, создаваемых подзонам в точке Р, медленно убывают. В пределе при стремлении числа подзон к бесконечности ломаная линия перейдет в непрерывную спираль, закручивающуюся к точке (фокусу) F (рис. 8. , б и в). Эту спираль называют спиралью Френеля.

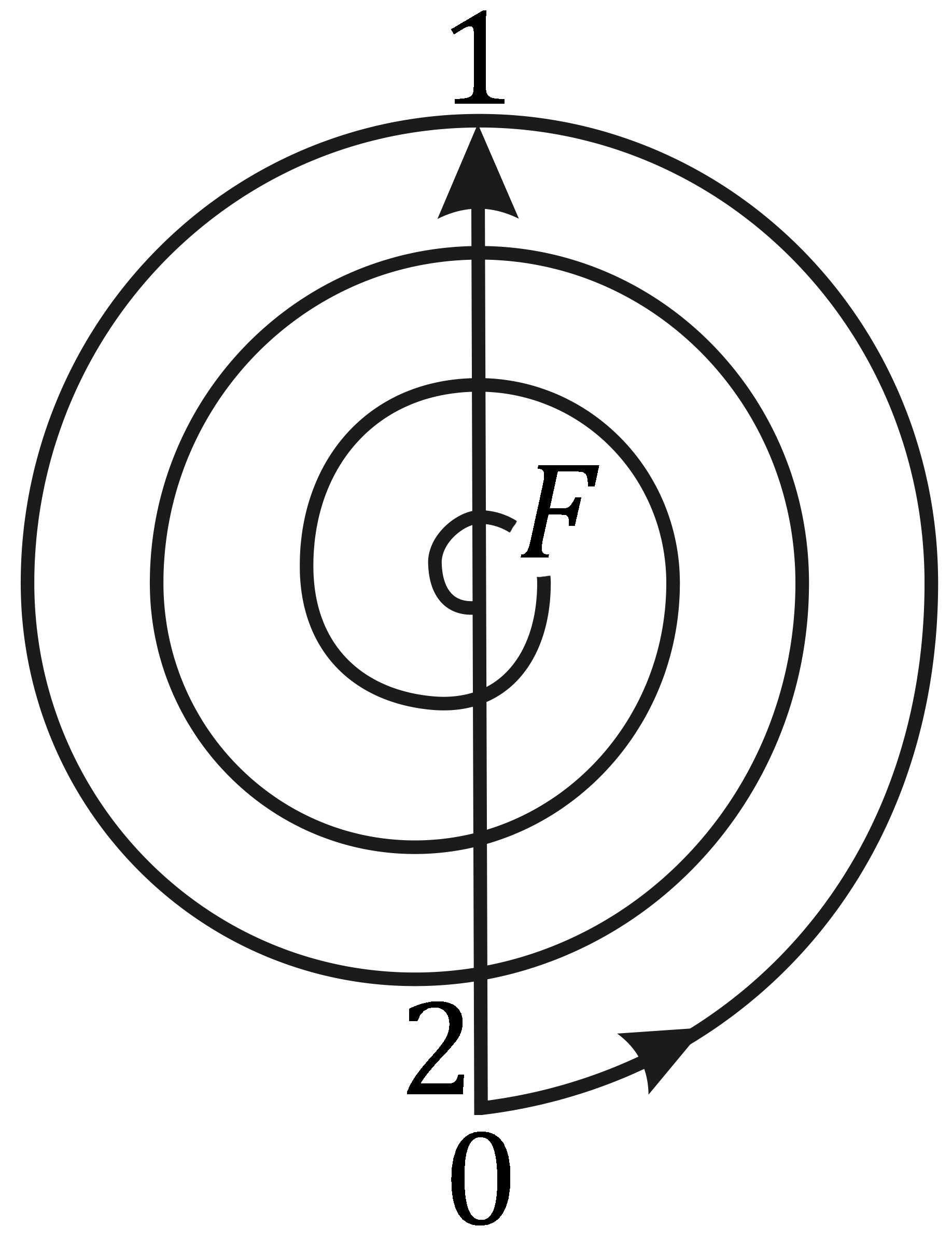
Точкам 0 и 1 спирали на рис. 8. , б соответствуют фазы колебаний, отличающиеся на π (бесконечно малые векторы, образующие спираль, направлены в этих точках противоположно). Поэтому участок 0–1 спирали соответствует первой зоне Френеля (очевидно, что каждой зоне Френеля соответствует полуокружность), Вектор, проведенный из точки 0 к точке 1, изображает колебание в точке Р этой зоной. Вектор, проведенный из точки 1 в точку 2, изображает колебание, создаваемое второй зоной Френеля, а вектор, проведенный из точки 0 к точке 2, представляет совместное действие двух первых френелевских зон и т.д.

а) б) в)

Рис. 6.8

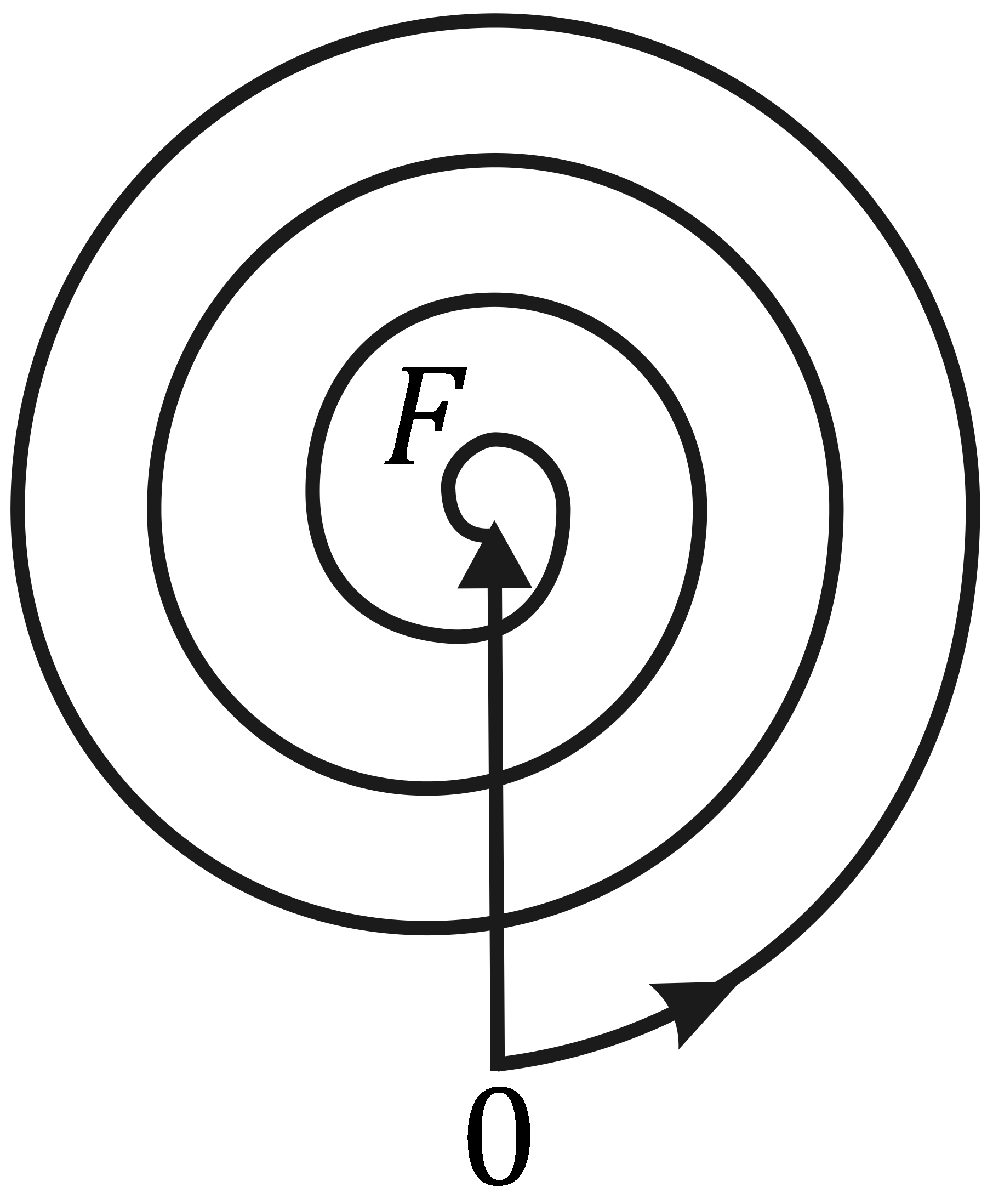
Точкам 0 и 1 спирали на рис. 8. , б соответствуют фазы колебаний, отличающиеся на π (бесконечно малые векторы, образующие спираль, направлены в этих точках противоположно). Поэтому участок 0–1 спирали соответствует первой зоне Френеля (очевидно, что каждой зоне Френеля соответствует полуокружность), Вектор, проведенный из точки 0 к точке 1, изображает колебание в точке Р этой зоной. Вектор, проведенный из точки 1 в точку 2, изображает колебание, создаваемое второй зоной Френеля, а вектор, проведенный из точки 0 к точке 2, представляет совместное действие двух первых френелевских зон и т.д. Колебание, возбуждаемое в точке Р всем волновым фронтом, изображается вектором, проведенным из точки 0 к точке F.

а) б) в)

Рис. 6.9

Как видно из рис. 6. , в, этот вектор почти точно вдвое короче вектора 01. Это означает, что амплитуда поля, создаваемая всем волновым фронтом, равна половине амплитуды, создаваемой первой зоной Френеля – в полном соответствии с приведенным выше алгебраическим расчетом.

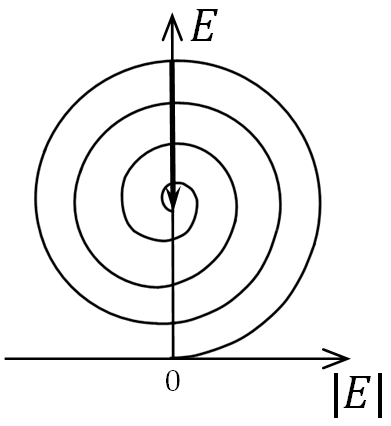
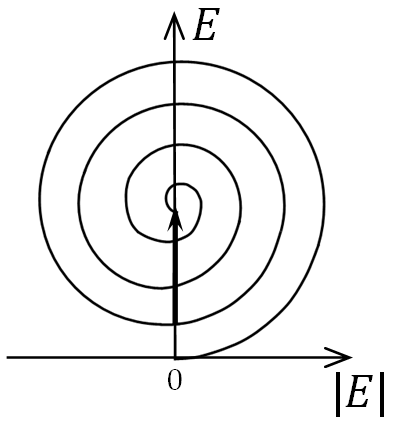
Применим метод векторных диаграмм к рассмотрению дифракции плоских волн на круглом отверстии и диске. В качестве точки наблюдения, как и прежде, выберем точку Р, расположенную на оси отверстия (и диска). На рис. 6. показаны построения спиралей

Рис. 6.10

Френеля, выполненные для случаев, когда в отверстии укладывается разное число зон Френеля: одну (а), две (б), три (в). Используя результаты этих построений и формулу (8.5) для радиуса френелевых зон, можно получить зависимость амплитуды результирующего поля в точке Р от радиуса ρ отверстия. Эта зависимость показана на рис. 6.10.

а) б) в)

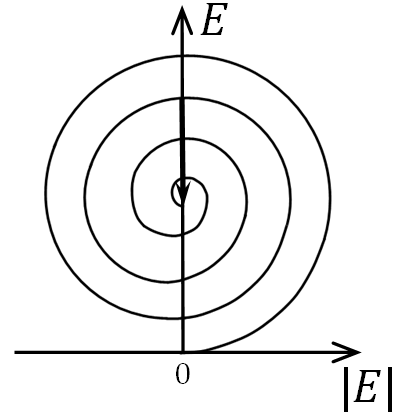
Рис. 6.11

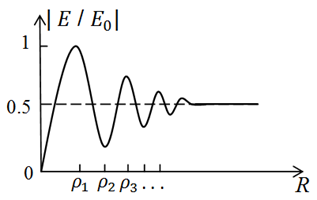
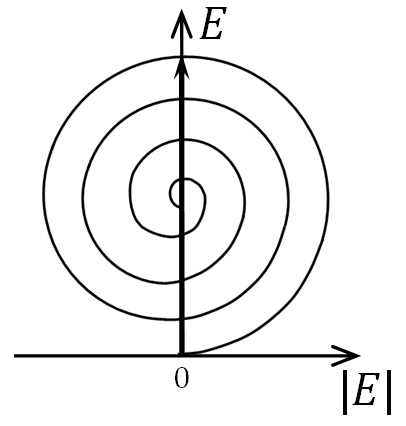
Из графика видно, что амплитуда светового поля в зависимости от радиуса отверстия является немонотонной Функцией, она совершает затухающие осцилляции относительно половинного значения амплитуды поля в отсутствие экрана. Максимальная интенсивность света в точке Р достигается, когда отверстие открывает только первую зону Френеля. В этом случае амплитуда поля в два раза, а интенсивность света в четыре раза больше, чем в отсутствие экрана. Далее максимум (но ниже первого) наблюдается, когда открыто три зоны Френеля (вообще при нечетном чис

Рис. 6.12

ле зон). Минимум в точке Р имеет место, когда отверстие открывает две зоны (и вообще четное число зон).

Построение спиралей Френеля для дифракции плоской волны на диске показано на рис. 6. Построения выполнены для случаев, когда диск закрывает первую зону Френеля (а), первую и вторую зоны (б) и первые три зоны (в). На рис. 6. изображена зависимость амплитуды светового поля в точке наблюдения Р от радиуса диска. В данном случае амплитуда поля является монотонно убывающей функцией, так что чем больше радиус диска, тем меньше интенсивность света в точке наблюдения. При этом, однако, интенсивность света в центре геометрической тени отлична от нуля даже в том случае, когда экран закрывает не одну, а несколько френелевых зон.