6.3. Дифракция Френеля на круглом отверстии и

диске

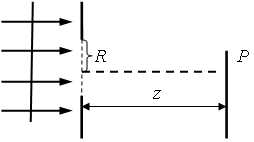
Применим метод зон Френеля к решению задач дифракции на простейших препятствиях – на круглом отверстии и диске. Рассмотрим случай плоских волн. Пусть на экран с круглым отверстием радиуса R падает плоская волна (рис. 6.4). Найдем ампли-

Рис. 6.

туду светового поля в точке Р, расположенной за экраном на прямой, на расстоянии z от экрана и центр отверстия. Участок фронта волны, вырезаемый круглым отверстием, будет представлять собой круг радиуса R. Его мы и выберем в качестве вспомогательной поверхности . Ясно, что в точке Р будет действовать только этот участок, поэтому построение зон Френеля следует производить только до краев отверстия. Число зон N в этом случае будет ограничено. Это число можно найти, приравняв радиус отверстия R радиусу N-ой зоны Френеля, т. е. считая, что _N = R. Тогда получим

N = . (7.6)

Поле в точке Р определится рядом с конечным числом членов N:

Е(Р) = Е₁ – Е₂ + Е₃ – … 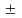Е_N , (7.7)

где перед Е_N ставится знак плюс при нечетном N и минус при четном N. Используя соотношение (3.3), находим

Е(Р) = Е₁ + Е_N при нечетном N и

Е(Р) = Е₁ + Е_{N –1} – Е_N при четном N.

Учитывая, что Е_N  Е_{N –1}, эти равенства можно объединить и записать

Е(Р) = Е₁ Е_N ,

где знак плюс соответствует не четному значению N и минус – четному N. Таким образом, если при заданных значениях a, R и  расстояние b таково, что число зон Френеля N, укладывающихся в отверстии, нечетное, то амплитуда поля в точке P будет больше, чем амплитуда поля при полностью открытом волновом фронте, а если это число четное – меньше. Наибольшее значение имеет амплитуда в той точке Р, для которой в отверстии укладывается всего одна зона, тогда Е(Р) = Е₁, т.е. вдвое больше, чем при полностью открытом фронте. Если для некоторой точки отверстие открывает две зоны, то, учитывая, что E₁  E₂, будем иметь E(P)  0. Амплитуда поля в такой точке будет иметь наименьшее значение.

При удалении от точки P в перпендикулярном к линии SP направлении одни зоны будут частично закрываться, а другие – частично открываться, поэтому амплитуда будет периодически изменяться, переходя от максимума к минимуму и наоборот. В результате на экране, расположенном перпендикулярно к линии SP, будет наблюдаться дифракционная картина в виде чередующихся светлых и темных колец с центрами в точке Р.

Совершенно аналогично в методе зон Френеля рассматривается дифракция на круглом отверстии и сферических волн. При этом получаются те же результаты, что и в случае сферических волн.

Положения максимумов и минимумов на оси Z, проходящей вдоль отрезка SP, по методу зон Френеля можно найти с помощью формулы (8.5), положив в ней z = z_m, R = _m и заменив m на 2m –1 для максимума и на 2m – для минимума. Получим координаты максимумов: z_m = R² / [(2m – 1)] и минимумов: z_m = = R² / (2m), m = 1, 2, 3, …

Дифракционная картина будет наблюдаться в окрестности точки Р, если для этой точки в отверстии будет укладываться хотя бы две зоны Френеля. Для этого расстояние от края зоны до точки Р должно быть равно M₂P = z +2 , где z – расстояние от центра отверстия до точки Р, т.е. если выполняется условие R² = (z + + )² – z²  2z , или с точностью до несущественного коэффициента 2: z  R² /, где R – радиус отверстия. Полученное соотношение представляет собой условие дифракции Френеля.

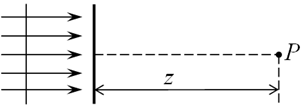
Пусть теперь на пути плоской или сферической волн установлен круглый диск и требуется определить амплитуду светового

Рис. 6.6

поля в точке Р, расположенной на оси диска на расстоянии z от него(рис. 6.). Если радиус диска R = _N , то он закрывает N первых зон Френеля. В этом случае ряд, определяющий амплитуду поля в точке Р, будет начинаться с (N +1)-го члена:

Е(P) = Е_{N +1} – Е_{N +2} + Е_{N +3} –…

В случае сферического волнового фронта число членов этого ряда бесконечно. Представляя его в виде

Е(P) = Е _{N +1} + + …,

получим: Е(P) = Е_{N +1}  0 при любом z и радиусе диска R. Таким образом, амплитуда, а значит, и интенсивность света нигде за диском в нуль не обращается. Это означает, что в любой точке Р, расположенной напротив центра диска, всегда будет наблюдаться светлое пятнышко. Оно называется пятном или диском Пуассона. Для точек, расположенных вне оси диска, суммарная амплитуда будет больше или меньше в зависимости от того, какая часть зон окажется закрытой. Поэтому светлое пятнышко в центре его геометрической тени будет окружено темными и светлыми кольцами.

Полученные результаты находятся в резком противоречии с законом прямолинейного распространения света, согласно которому напротив диска всегда должна наблюдаться резкая геометрическая тень.

Если увеличивать радиус диска, будет увеличиваться и число перекрываемых диском зон N, а амплитуда E_{N +1} будет убывать. Точка Р при этом будет оставаться освещенной. Так будет до тех пор, пока диск не закроет достаточно большое число зон Френеля, т. е. пока не будет выполнено условие N  1. Лишь в этом случае станет справедливым утверждение геометрической оптики, согласно которому препятствие, перекрывающее луч SР, дает в точке наблюдения Р темноту (геометрическую тень). Условие N  1 с учетом (3.1) или (3.5) можно привести к виду R 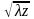 . Это условие определяет размер препятствия, при встрече с которым будет соблюдаться закон прямолинейного распространения света. Заметим, что это условие будет выполняться при любом размере препятствия R, если длина волны света  0. Однако не условие  0 (которое не выполняется), а соотношение R  или z  R² / можно считать основным условием выполнения закона прямолинейного распространения света.

Метод зон Френеля позволяет получить и условие наблюдения дифракции Фраунгофера. Дифракция Фраунгофера наблюдается, если расстояния a и b велики (в пределе a  и b  или z  при дифракции плоских волн).В этом случае, как следует из соотношения (3.6) или (3.5), N  1– отверстие открывает лишь малую часть первой зоны Френеля. Учтя это неравенство, положив в (3.6) для удобства a = b и обозначив эти расстояния через z, получим (с точностью до несущественного множителя) условие наблюдения дифракции Фраунгофера: z  R² /. Величину R² / называют дифракционной длиной светового пучка и обозначают z_д. Под R при этом понимают радиус светового пучка. Величину N_F = R² / z называют числом Френеля.

Используя результаты, полученные в этом параграфе, можно установить количественный критерий, позволяющий определить, какой вид дифракции (Френеля или Фраунгофера) будет иметь место в каждом конкретном случае, и критерий справедливости закона прямолинейного распространения света при встрече его с препятствием. Введем величину p, называемую параметром дифракции, определив его как отношение радиуса первой зоны Френеля к линейному размеру R препятствия: 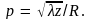Как легко убедиться, параметр дифракции Отсюда следует, что если параметр дифракции 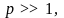, то имеет место дифракция Фраунгофера, если 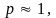– дифракция Френеля. Случай 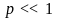соответствует геометрической оптике. Таким образом, параметр дифракции p полностью определяет характер дифракции и условие выполнимости закона прямолинейного распространения света. Он и дает искомый критерий.

Следует отметить, что при изменении расстояния z в q раз и размера отверстия R в раз значение параметра p останется прежним, а значит, и условия наблюдения дифракции останутся прежними. Следовательно, дифракционные картины, наблюдаемые в подобных условиях, так же будут подобными.