Задача 1.

Розв’язати задачу лінійного програмування симплексним методом:

1.1. ; 1.2. ;

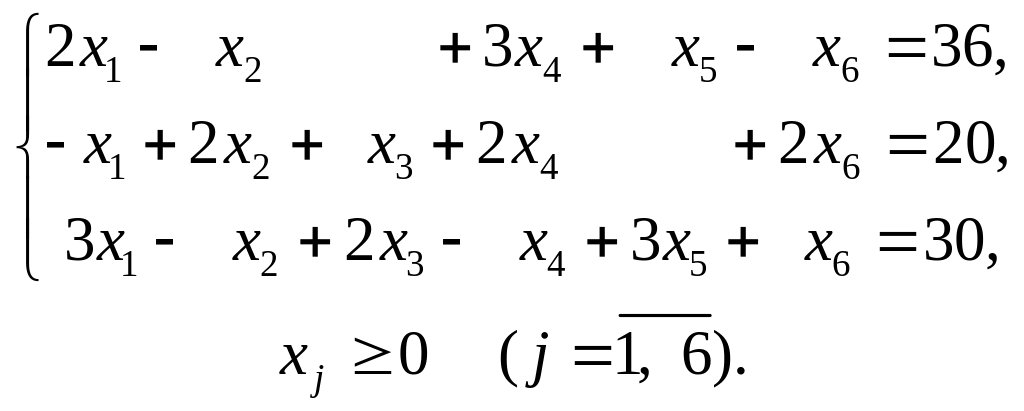
ДОДАТКОВІ ЗАВДАННЯ:

№1: Розв’язати задачу лінійного програмування симплексним методом:

1.1. ;

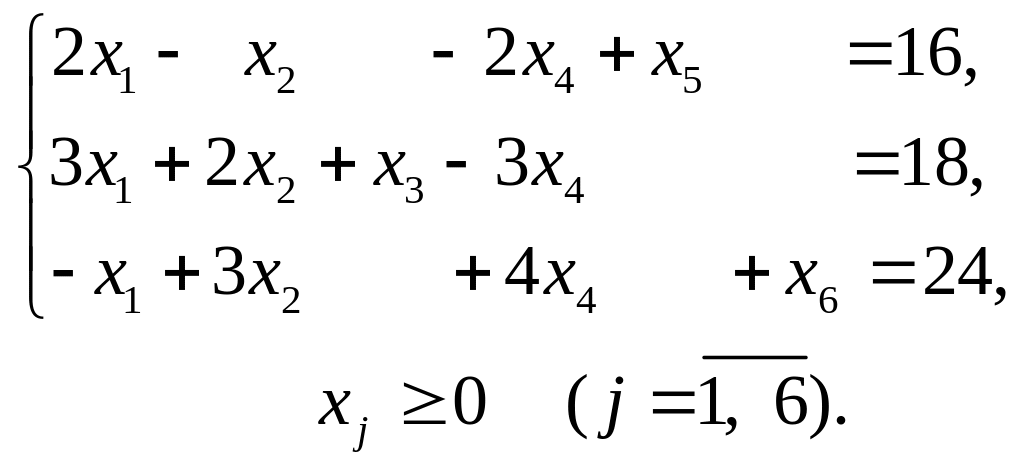
Тема 3. Задача лінійного програмування та методи її розв’язування. Лабораторне заняття №3

Тема заняття: Розв’язання задач лінійного програмування методом штучного базису.

Мета: сформувати вміння та навички розв’язування задач лінійного програмування методом штучного базису.

Методичні рекомендації: Вивчити лекцію №3 та ознайомиться з наступною літературою [1 с. 39-52], [2 c. 33-74], [3 с. 32-78].

Постановка завдання:

Теоретичні рекомендації вирішення задач ЛП зі штучним базисом наведені до лабораторної роботи 2, тому розглянемо вирішення задачі на прикладі.

Розв’язати приклад 1 із додатковою умовою: продукція С має виготовлятися в кількості не менш як 9 одиниць.

Розв’язування. Математичну модель сформульованої задачі запишемо так:

Застосовуючи для розв’язування поставленої задачі симплекс-метод, спочатку записуємо систему обмежень у канонічній формі, а далі — у векторній:

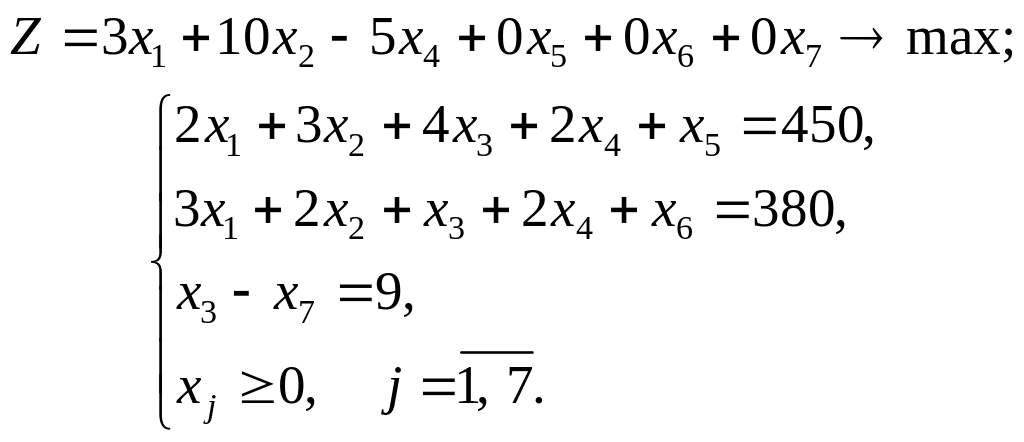
Зауважимо, що нерівність типу «≥» у рівняння перетворюємо введенням у ліву частину обмеження додаткової змінної зі знаком «–».

Векторна форма запису:

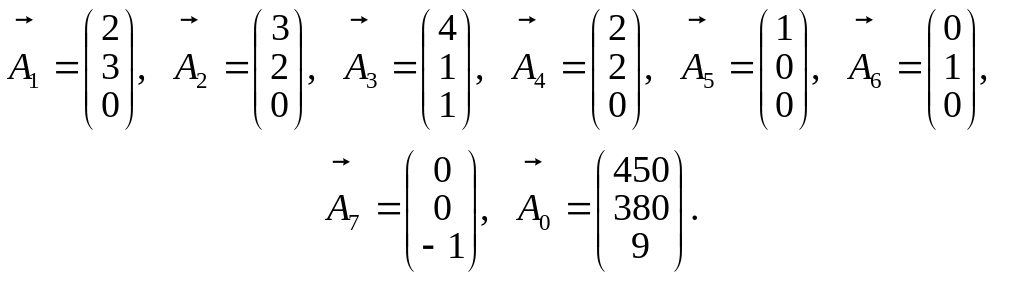
Серед записаних векторів є лише два одиничні — та , а базис у тривимірному просторі має складатися з трьох одиничних векторів. Ще один одиничний вектор можна дістати, увівши в третє обмеження з коефіцієнтом +1 штучну змінну х₈, якій відповідатиме одиничний вектор .

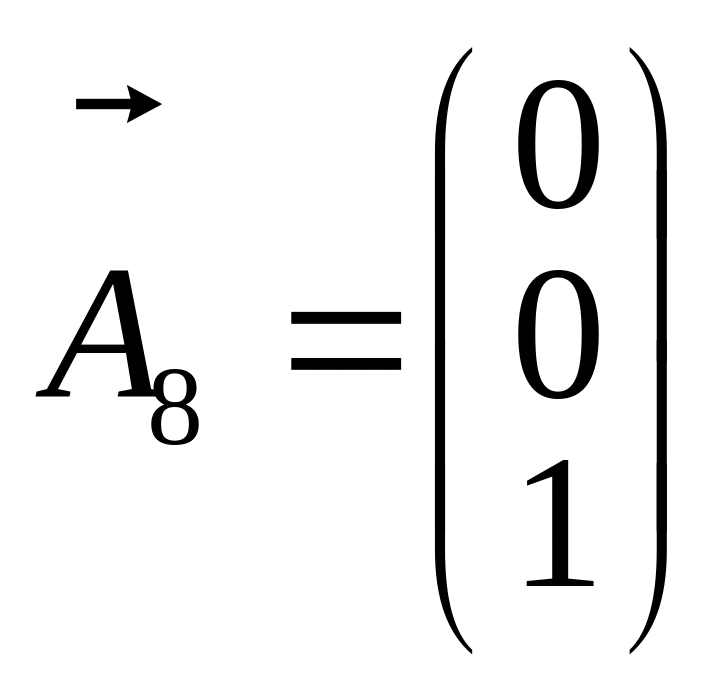Тепер можемо розглянути розширену задачу лінійного програмування:

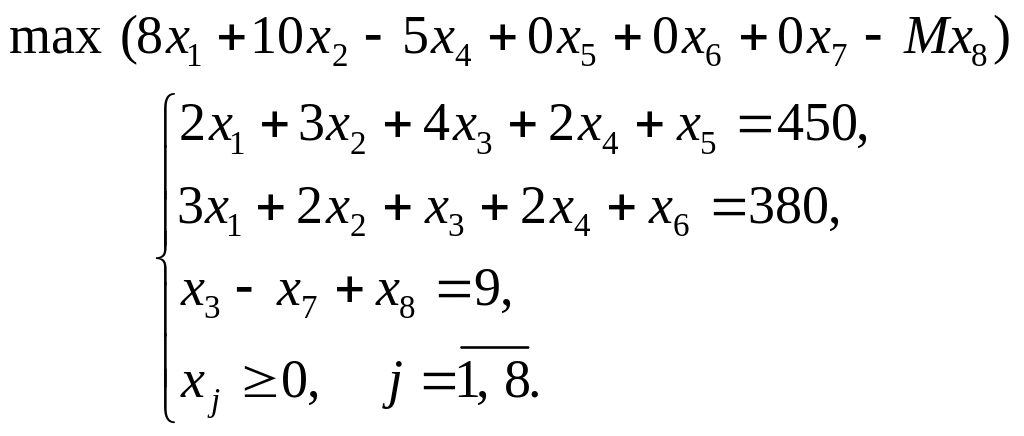
На відміну від додаткових змінних штучна змінна х₈ має в цільовій функції Z коефіцієнт +М (для задачі на min) або –М (для задачі на max), де М — досить велике додатне число.

У розширеній задачі базисними змінними є х₅, х₆, х₈, а решта змінних вільні. Початковий опорний план задачі:

Складемо першу симплексну таблицю задачі:

Базис	Сбаз	План	8	10	0	–5	0	0	0	–М	θ
			х1	х2	х3	х4	х5	х6	х7	х8
х5	0	450	2	3	4	2	1	0	0	0	112,5
х6	0	380	3	2	1	2	0	1	0	0	380
←х8	–М	9	0	0	1	0	0	0	–1	1	9
Zj – Cj ≥ 0		0	–8	–10	0	5	0	0	0	0
		–9М	0	0	–М	0	0	0	М	0

Розраховуючи оцінки першого опорного плану, дістаємо Z₀ = 0 – 9M, Z₁ – C₁ = –8, Z₂ – C₂ = –10, Z₃ – C₃ = 0 – М і т. д. Як бачимо, значення оцінок складаються з двох частин, одна з яких містить М, а інша — просто число. Тому для зручності розбиваємо оцінковий рядок на два. У перший оцінковий рядок записуємо просто число, а в другий — число з коефіцієнтом М.

Оцінки першого плану не задовольняють умову оптимальності, і тому він є неоптимальним. Згідно з алгоритмом, виконуємо перехід до наступного опорного плану задачі.

Подальше розв’язування задачі наведене у вигляді таблиці:

Базис	Сбаз	План	8	10	0	–5	0	0	0	–М	θ
			х1	х2	х3	х4	х5	х6	х7	х8
← х5	0	414	2	3	0	2	1	0	4	–4	138
х6	0	371	3	2	0	2	0	1	1	–1	185,5
х3	0	9	0	0	1	0	0	0	–1	1	—
Zj – Cj ≥ 0		0	–8	–10	0	5	0	0	0	0
		0	0	0	0	0	0	0	0	М
х2	10	138	2/3	1	0	2/3	1/3	0	4/3	–4/3	207
← х6	0	93	5/3	0	0	2/3	–2/3	1	–5/3	5/3	57
х3	0	9	0	0	1	0	0	0	–1	1	—
Zj – Cj ≥ 0		1380	–4/3	0	0	35/3	10/3	0	40/3	–40/3
		0	0	0	0	0	0	0	0	М
х2	10	100	0	1	0	2/5	3/5	–2/5	2	–2
х1	8	57	1	0	0	2/5	–2/5	3/5	–1	1
х3	0	9	0	0	1	0	0	0	–1	1
Zj – Cj ≥ 0		1456	0	0	0	61/5	14/5	4/5	12	–12
		0	0	0	0	0	0	0	0	М

Оптимальним планом задачі є вектор

Х^* = (57; 100; 9; 0; 0; 0; 0),

Отже, оптимальним є виробництво 57 одиниць продукції А, 100 одиниць продукції В і 9 одиниць продукції С. Тоді прибуток буде найбільшим і становитиме 1456 дол.