Тема 1. Концептуальні аспекти математичного моделювання економіки.

Тема 2. Оптимізаційні економіко-математичні моделі. Лабораторне заняття №1

Тема заняття: Розв’язування задач міжгалузевого балансу.

Мета: сформувати вміння та навички розв’язування задач міжгалузевого балансу типу «витрати-випуск» з використанням вбудованих функцій програми Microsoft Excel.

Методичні рекомендації: Вивчити лекцію №1 та ознайомиться з наступною літературою [1 с. 13-35], [2 c. 5-32], [3 с. 6-30], [4 c.6-116].

Постановка задачі:

1. Використовуючи дані таблиці 1 «Витрати – випуск» обчислити:

0. 1.1. коефіцієнти прямих, непрямих та повних витрат;

1. 1.2. абсолютні та відносні прирости (падіння) валового випуску кожної галузі, якщо кінцеве споживання галузі І збільшиться на одиниць, а галузі ІІ - на 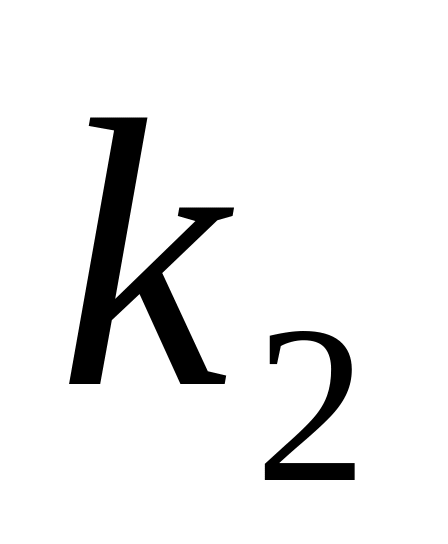одиниць.

2. За даними таблиці 2, яка для таблиці 1 відображає норми витрат ресурсів та відповідну їм вартість, визначити:

1. загальну витрату ресурсів на виконання виробничої програми;

2. коефіцієнти прямих витрат ресурсів на одиницю кінцевої продукції;

3. витрату ресурсів за галузями;

4. виробничі витрати в грошових одиницях по галузям і на всю виробничу програму;

5. виробничі витрати на одиницю кінцевої продукції.

Примітка: при обчисленнях скористатися вбудованими математичними функціями MS Excel: «СУММ» – для обчислення суми, «МУМНОЖ» – для обчислення добутку матриць, «МОБР» – для обчислення оберненої матриці.

Порядок розв’язання:

Таблиця 1

ВИТРАТИ – ВИПУСК

Галузі	Внутрішньовиробниче споживання			Кінцеве споживання
	І	ІІ	ІІІ
І
ІІ
ІІІ

де 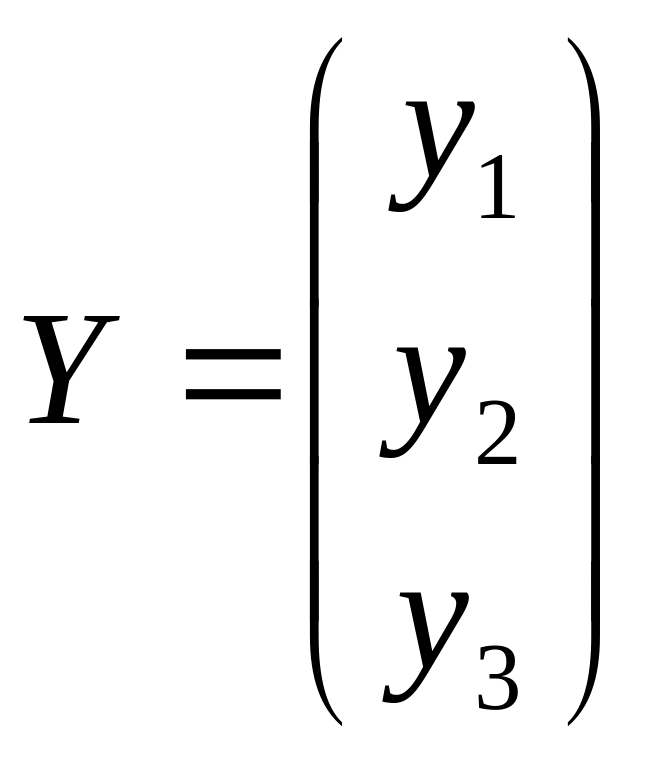- матриця кінцевого споживання

Для обчислення коефіцієнтів прямих, непрямих та повних витрат визначимо:

Валовий випуск кожної галузі за формулою: .

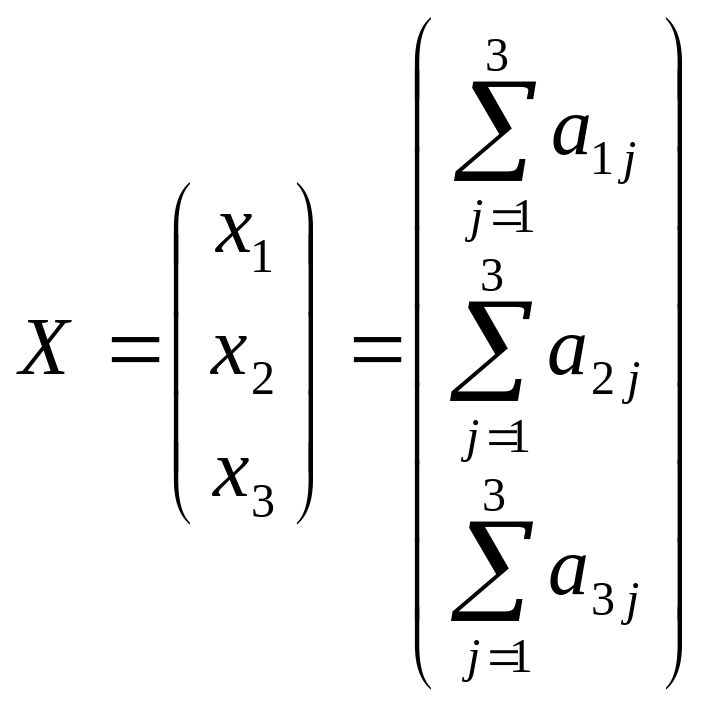Матрицю прямих витрат, як: .

Матрицю непрямих витрат за формулою: , де – одинична матриця

Для обчислення абсолютних та відносних приростів (падінь) валового випуску кожної галузі, якщо кінцеве споживання галузі І збільшиться на одиниць, а галузі ІІ - на одиниць визначимо:

Валовий випуск, якщо кінцеве споживання галузі І збільшиться на одиниць, а галузі ІІ - на за формулою: , де .

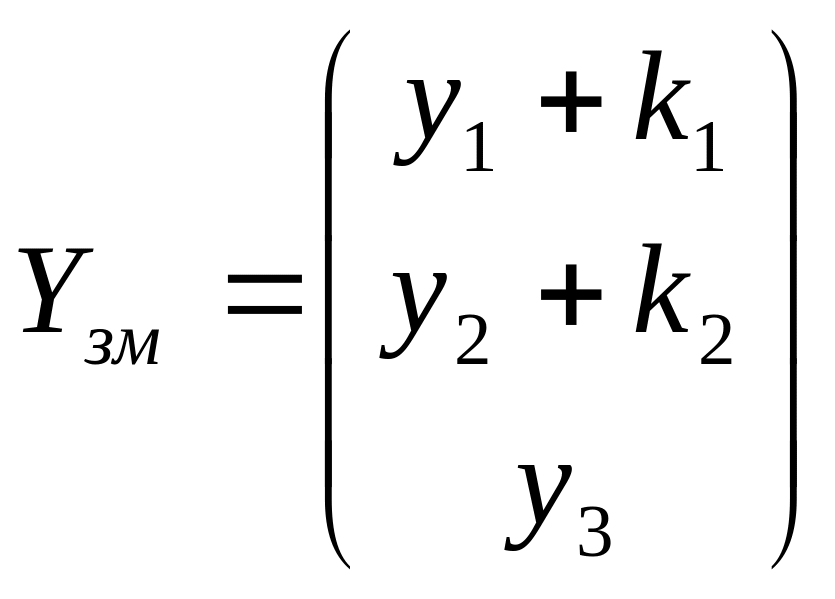Абсолютні прирости (падіння) за формулою: .

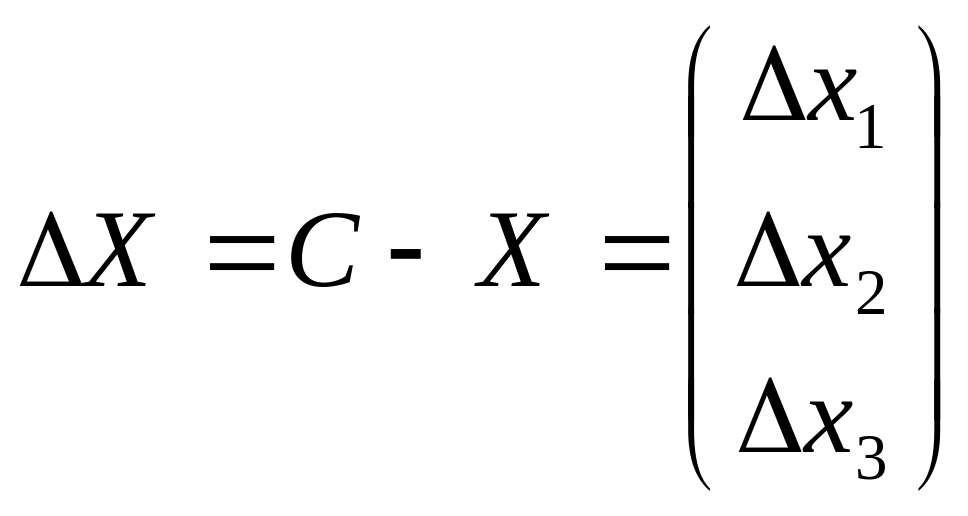Відносні прирости, як: .

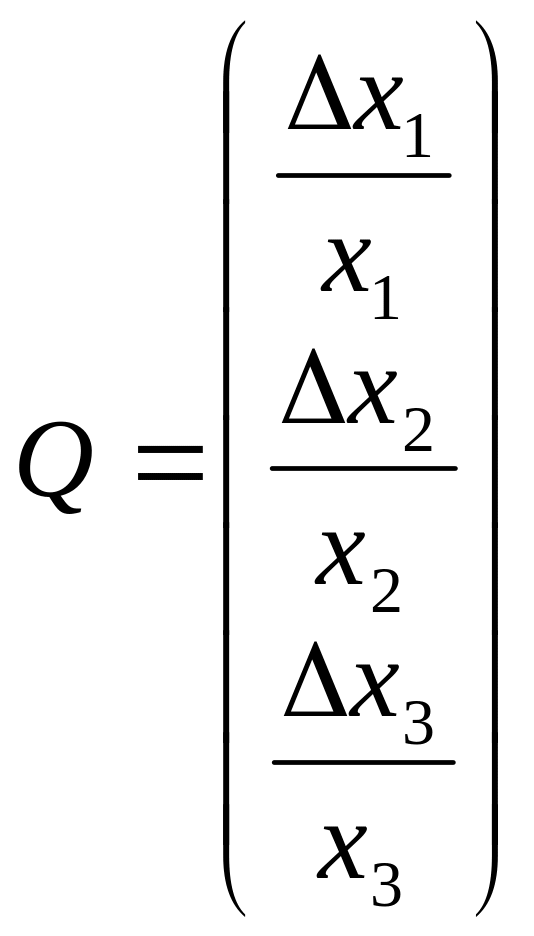Таблиця 2

НОРМИ ВИТРАТ РЕСУРСІВ

Ресурси	Прямі норми витрат			Вартість одиниці ресурсу
	І	ІІ	ІІІ
Сировина А
Сировина В
Паливо
Трудомісткість

де 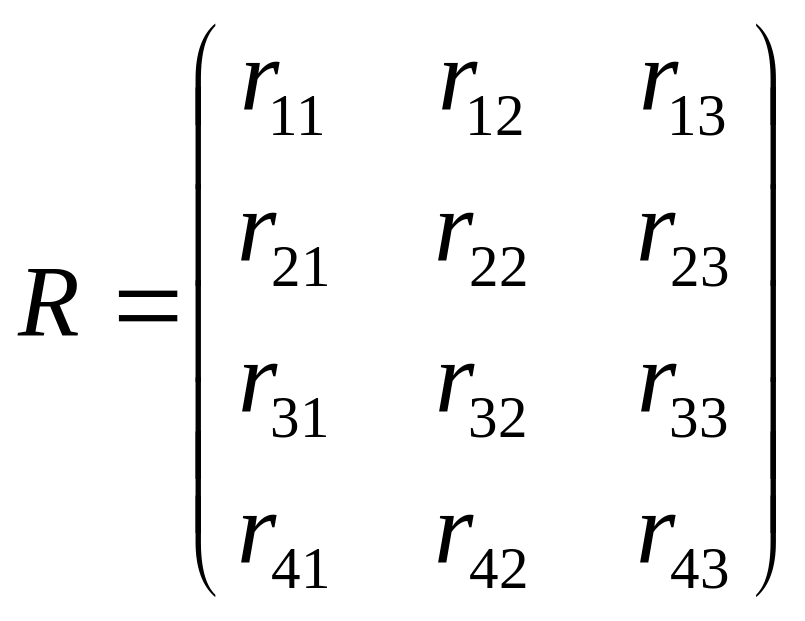- матриця норм витрат ресурсів.

Загальну витрату ресурсів на виконання виробничої програми визначимо як:

Коефіцієнти прямих витрат ресурсів на одиницю кінцевої продукції визначимо як:

Витрату ресурсів за галузями визначимо за формулою:

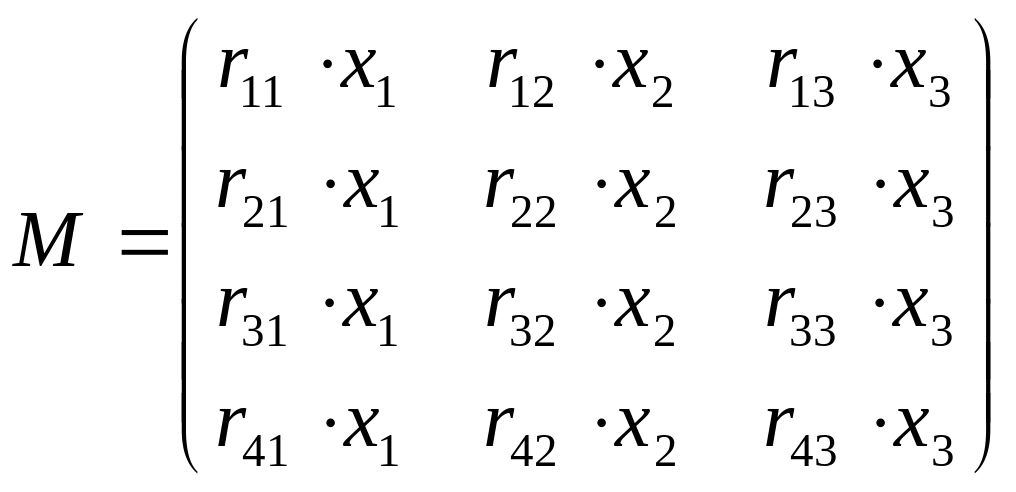
Виробничі витрати в грошових одиницях по галузям визначимо як: .

Виробничі витрати на одиницю кінцевої продукції визначимо як: .